Sul formalismo della meccanica quantistica

Giuseppe Garozzo

Abstract

In this paper we will briefly illustrate the historical development of Quantum Mechanism in connection to the philosophical point view of Empirism versus Rationalism. Our goal is to demonstrate that the usual Dirac formalism is the product of the Empirist approach to the problem to describe some experimental results. But it is clear that different approaches to same experiments produce different formalism.

Per comprendere il formalismo attuale della Meccanica Quantistica occorre tenere presente:

• Le conoscenze fisico-matematiche dei primi del ‘900

• La cultura ‘filosofica’ con cui tali conoscenze venivano interpretate.

Il quadro fenomenologico può essere schematizzato nella maniera seguente. Tutta una serie di fenomeni legati all’analisi degli spettri dei gas aveva mostrato che, qualora i gas fossero sufficientemente rarefatti, la luce emessa da questi gas (sottoposti ad una ‘scarica’) se analizzata da un reticolo di diffrazione (analizzatore di spettro, esempio prisma) mostrava delle righe luminose strette e ben distanziate. Ogni gas poi aveva una serie di righe di un dato colore; questa serie di righe luminose ‘era la carta d’identità’ del gas. Il dato interessante era che, mentre nello spettro della luce naturale il passaggio da un colore all’altro avviene con continuità, nei gas (rarefatti e sottoposti ad una scarica!) si osservavano righe ben delineate e ben equispaziate. Era la prima volta che i fisici avevano a che fare con valori di grandezze fisiche (cioè risultati di misurazioni) che si disponevano in maniera discreta? Certamente no, basti pensare alla fisica delle corde di violino (o similmente della chitarra). Il principio fisico su cui poggia il funzionamento della chitarra è il seguente. Una corda vibrante, qualora venga fissata ai due estremi, emette una serie di frequenze ben precise (mi, sol e così via), ovvero il suo spettro in frequenze risulta quantizzato.

Per questo motivo i fisici dell’epoca, quando si trovarono a trattare ‘quelle nuove grandezze il cui valore misurato in condizioni sperimentali ben precise (gas rarefatti e sottoposti ad una scarica) risultava quantizzato’, attinsero i modelli matematici dalla fisica dei fenomeni ondulatori (equazione delle onde).

Non bisogna dimenticare poi la profonda rottura che esisteva (ed esiste ) fra meccanica classica ed elettromagnetismo. Infatti, mentre la meccanica classica era (ed è) una teoria fondata sull’interazione a distanza, l’elettromagnetismo è una teoria di campo puro la quale, come sosteneva Hertz, coincide con lo studio matematico delle equazioni (fenomenologiche) di Maxwell. E appunto questa mancata coerenza delle due teorie che portava (e porta) ai paradossi più noti (il problema del corpo nero, l’effetto fotoelettrico, l’effetto Compton e la presunta instabilità dell’atomo di idrogeno). Infatti nessuno può negare che tutte le contraddizioni nascevano (e nascono) quando si mescolavano alcuni risultati della meccanica classica con altri dell’elettromagnetismo. In effetti quando si parla di fisica classica, intendendo con questo termine la meccanica di Newton e la teoria di Maxwell, si compie un abuso filosoficamente inaccettabile.

Si è soliti far iniziare la nascita della meccanica quantistica il 14 Dicembre del’900 quando Planck espose la sua teoria dello spettro del corpo nero alla Società Tedesca di Fisica. Egli, in sintesi, osservò che per trovare una curva che ben ‘fittasse’ (si adattasse a) i dati sperimentali era sufficiente introdurre una costante di parametrizzazione h (il cui valore veniva determinato fenomenologicamente come valore che minimizza la differenza fra la curva sperimentale e quella teorica), e ciò era equivalente ad asserire che l’energia di un oscillatore armonico isolato (si pensi ad un corpo legato ad una molla) è proporzionale alla frequenza (proposizione a: E = h v) e può assumere solo valori del tipo En = nhv dove v è la frequenza fondamentale ed n è un intero positivo (proposizione b).

Oggigiorno è stato mostrato che la proposizione a risulta vera in meccanica classica per oscillatori armonici ‘perturbati’ (vedere teoria degli invarianti adiabatici¹), e che esistono molti modelli classici che spiegano bene lo spettro del corpo nero e che quindi riottengono la proposizione b².

E per gli altri fenomeni sono state trovate spiegazioni alternative?

La risposta è: per alcuni si, per altri no; c’è pure chi sostiene che ancora non è stato trovato un fenomeno puramente quantistico (alcuni sostengono che la superconduttività è un fenomeno puramente quantistico, anche se è stato scoperto molto prima della meccanica quantistica ed attualmente esiste anche un modello classico di superconduttività³).

Tuttavia, è fuor di dubbio che l’aspetto ondulatorio dei fenomeni di diffrazione dei fasci di elettroni è quello che colpisce più di tutti; furono appunto le proprietà ondulatorie della materia (nel senso specificato prima) a spingere i fisici dell’epoca a cercare una nuova teoria. Fu De Broglie a capire (capire, intuire o che altro?) che le particelle presentavano pure un aspetto ondulatorio. L’ipotesi di De Broglie di associare una lunghezza d’onda ed una frequenza alle particelle può sembrare una trovata originalissima. Per trattare esaurientemente tale idea, come storicamente si è formata, occorrerebbe far ricorso alla teoria della relatività (con la sua annessa teoria dei fotoni). Tuttavia ci limitiamo a dire che, poichè la fenomenologia che si presentava all’epoca era molto simile a quella delle corde vibranti (nel senso che le grandezze misurate erano per lo più discrete) non c’è da stupirsi se sul piano fisico si è voluta spingere tale analogia fino ai costituenti elementari della materia. Peraltro l’ipotesi di De Broglie era la prima ipotesi sufficientemente generale che poteva giustificare alcune regole di calcolo stabilite ad hoc per spiegare gli spettri atomici (le famose regole di quantizzazione di Bohr-Sommerfield; ad esempio: la quantizzazione del momento angolare per le orbite elettroniche).

Pertanto possiamo riassumere quanto abbiamo detto nei seguenti punti:

- Comparsa di grandezze fisiche il cui valore misurato è discreto;

- Solo la fisica delle onde (es. corda di chitarra) offre una fenomenologia simile;

- Regole di calcolo ad hoc per giustificare alcuni risultati sperimentali (Planck, Bohr-Sommerfield);

- Ipotesi di Be Broglie sui costituenti elementari della materia che permette di giustificare quelle regole di calcolo.

Interviene poi un ulteriore elemento. Le grandezze fisiche ‘lunghezza d’onda’ e ‘frequenza’ sono delle grandezze fisiche particolari. Per esempio, se io dico che la stecca da biliardo misura 2 m, significa che essa è due volte il mio campione di lunghezza che posso riportare sulla stecca e verificare che ci sta due volte. Le cose sono un po’ più complicate per la lunghezza d’onda (e similmente per la frequenza).

Tali grandezze fisiche vengono definite a partire dalle soluzioni di una data equazione (equazione delle onde). Infatti una semplice soluzione di una equazione d’onda, come quella di D’Alembert (chiaramente esistono più equazioni d’onda), è del tipo:

Questa soluzione si riscontra ad esempio nel caso di una perturbazione data in un punto di una corda vibrante che si propaga lungo la curva stessa. Se fissiamo il tempo (per semplicità poniamo t = 0) il grafico della soluzione sarà:

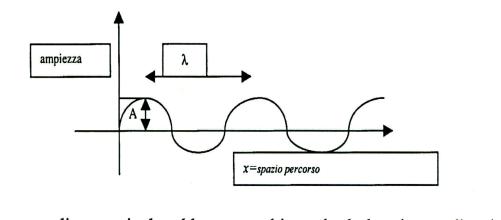
Da questo disegno risulta abbastanza chiaro che la lunghezza d’onda è la distanza spaziale (ideale) fra due creste. Ci si potrebbe chiedere, quante creste passano in un secondo in un dato punto dello spazio; in pratica, il numero di creste che passano in un secondo in un dato punto della corda è la frequenza dell’onda, ovvero la distanza temporale fra due creste.

Queste due grandezze fisiche poi possono essere determinate sperimentalmente solo mediante misurazioni indirette che richiedono tutta una teoria dell’esperimento. Cioè non è possibile metterci con un metro a cavallo dell’onda e determinare la distanza fra le creste!

Nell’ambito dei fenomeni luminosi si possono usare i fenomeni dell’interferenza e della diffrazione (fenomeni che richiedono per la loro comparsa l’utilizzo di ben determinati accorgimenti sperimentali, ad esempio reticoli di diffrazione di passo opportuno. Un reticolo di diffrazione lo si può pensare come una griglia fitta, in cui lo spazio fra una finestra e la successiva è detto passo) per potere risalire alla lunghezza d’onda ed alla frequenza dell’onda.

Quindi, riassumendo:

Le grandezze fisiche lunghezza d’onda e frequenza sono definite a partire dalle soluzioni di determinate equazioni note come equazioni delle onde; la loro determinazione sperimentale può effettuarsi solo mediante degli esperimenti costruiti appositamente e fondati sulla teoria matematica dell’equazione delle onde.

Ci manca un altro importante tassello. Infatti la teoria (matematica) delle equazioni delle onde ci dice che la soluzione più generale di una tale equazione è data dalla sovrapposizione di infinite soluzioni particolari semplici dette onde armoniche che poi sono delle semplici funzioni sinusoidali che hanno dunque una lunghezza d’onda ed una frequenza ben definita; cioè per l’equazione delle onde vale il principio di sovrapposizione delle onde. Per essere precisi esso non è un principio bensì un teorema di matematica. Questo teorema è importante perché fu la chiave di volta per comprendere il fenomeno della dispersione della luce bianca (cioè quella solare) attraverso un prisma. Infatti quello che accade è che in entrata (rispetto al prisma) la luce è incolore, in uscita invece si osservano tutti i colori dell’arcobaleno in successione (e con continuità).

Come si spiega questo fenomeno?

Ebbene si dice che la luce è descritta da una funzione, soluzione di una equazione d’onda, e come tale questa funzione è la sovrapposizione di tante onde semplici (sinusoidali , cioè che hanno una ben determinata frequenza e lunghezza d’onda); poi, quando questo miscuglio di onde attraversa il prisma, si separano e dunque è possibile distinguerle in uscita.

Nessuno tuttavia può affermare che il miscuglio di onde semplici esiste prima dell’interazione col prisma; è possibile infatti sostenere che le onde in uscita vengono create dall’interazione col prisma. Questo è un punto cruciale: il prisma è un filtro o un preparatore di stato? Cioè è uno strumento che evidenzia la struttura intrinseca della luce (filtro), oppure è uno strumento che partecipa alla creazione di quella data struttura del fascio in uscita (preparatore di stato)?

La risposta a questa domanda non può trovarsi sul piano sperimentale!

La teoria matematica delle equazioni delle onde ci permette di parlare di sovrapposizione di onde sinusoidali prima che l’onda incida sul prisma, ma affidarsi ad una tale interpretazione rimane sempre una questione di mero gusto.

A questo punto siamo in grado di introdurre l’ultimo tassello. Infatti se una particella (si badi che la teoria con la quale parliamo [e si parla] per costruire la quantistica è la meccanica classica!) è descritta in termini di lunghezza d’onda e frequenza è chiaro che il suo moto deve essere descritto da una equazione d’onda. Ebbene, il primo a proporre (non a dedurre, ripeto, proporre) una equazione d’onda per descrivere il moto delle particelle fu Schrödinger. La sua famosa equazione, detta appunto equazione di Schrödinger, descrive l’evoluzione temporale dell’onda associata alla particella nota come funzione Ψ(r) (con r punto dello spazio fisico). Ebbene, risolvendo questa equazione nel caso di un sistema elettrone-protone (atomo di idrogeno), Schrödinger fu in grado di predire lo spettro dell’atomo di idrogeno (fenomenologicamente già conosciuto!): fu un vero trionfo! Come tutte le equazioni d’onda l’equazione di Schrödinger presenta un parametro (che nel caso appunto dell’equazione di Schrödinger è l’energia) il quale condiziona la possibilità di avere delle soluzioni. Infatti, matematicamente si dimostra che solo per certi valori del parametro energia, E,(valori che nel caso dell’atomo di idrogeno sono discreti) esistono delle soluzioni per la Ψ.

Ebbene, ordinati con E₁ , E₂ , E₃ ,.... E_N , ... i valori del parametro, le soluzioni corrispondenti saranno Ψ ₁ , Ψ ₂ , Ψ ₃ ,.... Ψ _N , ... Si usa chiamare il parametro E autovalore e la funzione corrispondente autofunzione.

L’insieme dei valori che può assumere l’autovalore, cioè E₁ , E₂ , E₃ ,.... E_N , ..., è detto spettro. Chiaramente se lo spettro è discreto l’insieme delle autofunzioni, cioe Ψ ₁ , Ψ ₂ , Ψ ₃ ,.... Ψ _N , ..., detto anche autospazio, risulta pure discreto. In generale però la corrispondenza fra autovalori e autofunzioni non è sempre di uno ad uno, ma questo è un problema che qui non affronteremo.

Quindi possiamo dire che lo spettro dell’energia dell’atomo di idrogeno è discreto così come possiamo dire che lo spettro delle frequenze della corda di una chitarra è discreto.

L’equazione delle onde di Schrödinger è il modello matematico con cui è possibile studiare la fisica atomica. Però chiaramente si pone il problema di interpretare tale equazione. Ovvero, la funzione d’onda cosa descrive? Due sono le principali risposte date:

• La funzione Ψ(r) descrive un’onda ontologicamente esistente che accompagna la particella durante il suo moto; la particella, poi, ha probabilità massima di occupare il punto dello spazio in cui il modulo quadro dell’onda (ovvero il quadrato dell’ampiezza dell’onda) è maggiore.

• La funzione Ψ(r) è una funzione il cui modulo al quadrato (cioè il quadrato della sua ampiezza) dà la probabilità di trovare la particella.

Quale delle due interpretazioni è quella più verosimile? Anche in questo caso è solo una mera questione di gusto (anche se la prima è più impegnativa sul piano ontologico...).

Le cose si complicano ulteriormente quando si tenta di interpretare il principio di sovrapposizione (cioè quel teorema che abbiamo precedentemente introdotto). Infatti (nel caso dell’atomo di idrogeno precedentemente citato) la soluzione generale della equazione di Schrödinger è data dalla somma di tutte quelle particolari, cioè

Ψ(r) = c₁ Ψ₁ (r)+ c₂ Ψ₂ (r)+ c₃ Ψ₃ (r)+ ……+c_N Ψ_N (r) ……,

ma in genere quando si fa una misura di solito si ottiene solo un ben determinato valore (le cose sono un po’ più complicate, in effetti non è sempre vero, ma facciamo finta di sorvolare...), e allora?

L’idea è quella di interpretare le costanti c_i come pesi. Ovvero se ad esempio c₁è maggiore di c₂ diciamo che abbiamo una probabilità maggiore di trovare sperimentalmente il valore E₁ dell’energia (cioè l’autovalore E₁) relativo all’autofunzione Ψ₁ che l’autovalore E₂ relativo all’autofunzione Ψ₂ . Più precisamente si asserisce che il modulo al quadrato delle c_i fornisce la probabilità che il sistema fisico oggetto della nostra misura sia nello stato descritto dall’autofunzione Ψ_i e che dunque il risultato della misura sia E_i. Si usa anche chiamare Ψ_i autostato (sinonimo di autofunzione). Questa interpretazione probabilistica delle costanti c_i giustifica l’interpretazione probabilistica della funzione d’onda data precedentemente (anche se non ci permette di scegliere fra le due interpretazione, ovviamente).

L’interpretazione probabilistica delle c_i, al di là delle pretese ontologiche, permette di dare una interpretazione coerente dei risultati che si possono ottenere risolvendo l’equazione di Schrödinger, che ricordiamo non è stata dedotta ma solo proposta perché funziona!

Che cosa vogliamo dire quando diciamo che l’equazione di Schrödinger è un modello?

Il discorso è che fino a questo punto manca una teoria organica dalla quale ricavare, o almeno entro cui inserire coerentemente, l’equazione di Schrödinger. Certo abbiamo fatto molti passi in avanti, dalle regole ad hoc per spiegare gli spettri atomici, siamo passati all’ipotesi di De Broglie consistente nell’associare un’onda ad una particella; ed ora abbiamo un assunto più forte e cioè che ad ogni particella è associata un’onda ψ e che tale onda obbedisce all’equazione di Schrödinger. Ma manca sempre una teoria di sfondo più coerente.

Allora interviene di nuovo la filosofia. Come facciamo a giudicare se una teoria è più coerente o meno? Qui ci imbattiamo in un mare in tempesta. Quello che possiamo dire è che agli inizi del ‘900 la maggior parte dei fisici, influenzati dalle critiche di Mach, vedevano nella meccanica di Newton un esempio di teoria fortemente infettata dalla metafisica. Perché? Bé, basta ricordare la definizione di quantità di materia data da Newton la quale risulta lecita solo in una teoria puramente atomistica. Oppure si pensi all’interazione a distanza, questo orrido fantasma (orrido per Mach, ma non tutti la pensano come lui)! Il punto fondamentale è che la meccanica classica, anzi più precisamente, la Meccanica Razionale è una teoria integralmente ‘razionalistica’ in cui per la sua costruzione non si fa appello a nessun principio di natura sperimentale. Ma se da un lato, una presenza di fondamento empirico nella Meccanica Razionale era quello che faceva dire a D’Alembert: ‘rovinerebbe ogni certezza nella Meccanica riducendola a niente di più che ad una scienza sperimentale’, dall’altro lato, questa assenza era proprio quello che fisici come Heisenberg contestavano alla meccanica di Newton. Cioè, veniva contestato il fatto che la meccanica di Newton non era una scienza sperimentale! Anzi veniva osannato Mach per averla in parte aggiustata! Quindi se la Meccanica deve essere una scienza sperimentale è chiaro che queste nuove osservazioni nate dallo studio sperimentale condotto sugli spettri atomici devono entrare nella costruzione di una nuova Meccanica che possa inquadrare come nuova equazione del moto l’equazione di Schrödinger.

Sotto questa luce empiristica, tenteremo di costruirla nell’Appendice, dato che la lettura di quanto segue non lede la comprensione dell’articolo e risulta particolarmente ostica. Dedichiamo questa appendice a chi volesse apprendere le basi del linguaggio tecnico della meccanica quantistica o a chi conoscendo già tale semiotica ne volesse comprendere la semantica.

Appendice

Postuliamo che le grandezze fisiche di questa nuova teoria debbano essere definite per mezzo delle operazioni fisiche atte a determinarle. L’esempio più paradigmatico è la definizione di spin tramite l’esperimento di Stern e Gerlach (in breve S.G.). Tale esperimento consiste nell’inviare un fascio di atomi che hanno un solo elettrone nell’orbita più esterna attraverso un campo magnetico non omogeneo generato lunga una ben precisa orientazione (asse z, per semplicità). In teoria, se il momento angolare dell’elettrone fosse distribuito randomicamente, in uscita osserveremo una dispersione omogenea del fascio, indice del fatto che i vari atomi vengono ‘piegati’ verso tutte le direzioni.

Invece quello che accade è che il fascio in uscita dall’apparato S-G si divide in due soli fasci ben distinti! Uno verso l’alto e l’altro verso il basso.

Indichiamo con il simbolo

|+ñ á+|

l’apparato S.G. (opportunamente modificato) che fa emergere solo il fascio che si dispone in alto (d’ora in poi tale apparato di S.G., che fa emergere solo un unico fascio, lo denomineremo preparatore di stato; esso si ottiene dall’apparato precedente mascherando con una opportuna lamina il fascio che esce verso il basso), con il simbolo

|-ñ á-|

quello che fa emergere solo il fascio che si dispone verso il basso. Se nell’insieme dei preparatori di stato definiamo una somma (+) ed un prodofto (*) convenendo di attribuire alla somma il significato di ‘messa in parallelo’ dei due preparatori ed al prodotto quello di ‘messa in serie’ banalmente si avrà:

|+ñ á+| + |-ñ á-| = I

|+ñ á+| * |-ñ á-| = |+ñ á+| |-ñ á-| = 0 (1) (cassando il simbolo di prodotto)

|+ñ á+| * |+ñ á+| = |+ñ á+ | +ñ á+| = |+ñ á+|² = |+ñ á+| (2) (cassando anche una sbarretta)

|-ñ á-| * |-ñ á-| = |-ñ á- | -ñ á-| = |-ñ á-|² = |-ñ á-| (3)

avendo indicato con I il preparatore che dà in uscita tutto quello che entra e con 0 quello che sopprime tutto il fascio di ingresso.

Dato che pretendiamo che le grandezze fisiche coincidano con i valori della misura, risulta comodo rappresentarle sotto la seguente forma (converremo di indicare le grandezze fisiche così costruite con il simbolo ^ sopra una lettera maiuscola):

Ŝ = S₁ | +ñ á+ | + S₂ | -ñ á- |

dove con S₁ ed S₂ abbiamo indicato il risultato della misura, che in questo caso è una misura di momento angolare. I possibili valori sono solo due perché il fascio in uscita si divide solo in due componenti. Più esattamente si misura: ed . In definitiva si ha

.

Da quanto detto S₁ e S₂ altro non sono che i valori dello spettro della grandezza S ovvero gli autovalori. Ma le autofunzioni o autostati quali sono? Conveniamo di indicare col simbolo

| +ñ l’autostato che descrive il fascio che viene piegato verso l’alto;

| -ñ l’autostato che descrive il fascio che viene piegato verso il basso.

Quindi da quanto detto prima segue che lo stato generico del fascio prima del suo incontro con l’apparato S-G è

|Ψñ = c₁ | +ñ + c₂ | -ñ (principio di sovrapposizione).

Stiamo convenendo dunque che i due simboli | +ñ e | -ñ si sommano (come gli Ψ_i dell’equazione di Schrödinger) e si moltiplicano per numeri cioè per le c_i . Essi si possono anche moltiplicare fra di loro qualora il prodotto sia eseguito così:

a) | +ñ * | -ñ = á+ | -ñ = 0 (incompatibilità dei due stati)

b) | +ñ * | -ñ = á+ | +ñ = 1

c) | -ñ * | -ñ = á- | -ñ = 1

L’assioma a) stabilisce che i due stati sono mutuamente esclusivi. Poi

d) | +ñ * | Ψ ñ = á+ | Ψ ñ = c₁ á+ | +ñ + c₂ á+ | -ñ ® á+ | Ψ ñ = c₁

e) | -ñ * | Ψ ñ = á- | Ψ ñ = c₁ á- | +ñ + c₂ á- | -ñ ® á- | Ψ ñ = c₂

Riassumendo finora:

• ogni sistema fisico è definito dai suoi autostati (o autofunzioni);

• lo stato generico del sistema è la sovrapposizione dei vari autostati;

• fra gli stati è possibile definire un prodotto che associa a due stati un numero;

• gli stati (gli autostati sono un particolare tipo di stato) possono essere moltiplicati per numeri.

Per tali ragioni l’insieme di tutti i possibili stati che si ottengono combinando gli autostati è detto spazio degli stati; si dice pure che tale insieme è uno spazio vettoriale; perché appunto gli stati si comportano come vettori (cioè si sommano e si moltiplicano per dare un numero, cioè hanno il prodotto scalare). Il numero degli autostati possibili dà la dimensione dello spazio degli stati (sinonimo di spazio vettoriale). Nel nostro esempio abbiamo due soli autostati | +ñ e | -ñ e quindi si dice che il nostro spazio ha dimensione due.

Ma come visto nel caso dell’atomo di idrogeno il numero di autostati (autofunzioni) è numerabile ma infinito. In tal caso lo spazio vettoriale è detto spazio di Hilbert (in pratica lo spazio di Hilbert è uno spazio vettoriale di dimensione infinita).

Un generico stato di uno spazio di Hilbert si scriverà cosi:

|Ψñ = c₁ |Ψ₁ñ + c₂ |Ψ₂ñ +……+c_N |Ψ_Nñ + ……,

ovviamente sarà:

c_N = á Ψ_N | Ψ ñ á Ψ_i | Ψ_j ñ = 0 per i diverso da j e á Ψ_i | Ψ_i ñ = 1

Noti gli autostati possiamo scrivere la grandezza fisica; nel caso dell’energia dell’atomo di idrogeno si ha:

Ma cos’è esattamente l’ente áΨ_N | Ψ_Nñ nel caso dell’energia dell’atomo di idrogeno o l’ente |+ñ á+| che abbiamo già incontrato quando abbiamo parlato dello spin?

Riprendiamo l’esempio dello spin con l’apparato di Stern-Gerlach. Osserviamo che da quanto detto discende che:

| +ñ á+ | * | +ñ = | +ñ á+ | +ñ = | +ñ * 1 = | +ñ

| +ñ á+ | * | -ñ = | +ñ á+ | -ñ = | +ñ * 0 = 0

dove stavolta zero indica che non c’è alcuno stato.

Cioè matematicamente | +ñ á+ | è un ente che applicato al vettore | +ñ lo lascia invariato, mentre applicato al vettore | -ñ lo annulla. Un tale ente è detto operatore, cioé opera su di un vettore per dare un altro vettore. In particolare esso è un operatore di proiezione poiché verifica la seguente proprietà:

| +ñ á+ | Ψ ñ = c₁ | +ñ

cioè è quell’operatore che applicato al generico stato | Ψñ fornisce, a meno di una costante moltiplicativa un vettore di base (ovvero un autostato), cioè è come se proiettasse il vettore | Ψñ lungo una ben determinata proiezione (che è quella descritta da un autostato).

Quindi

| +ñ á+ | | -ñ á- | | Ψ_i ñ á Ψ_i |

sono tutti operatori di proiezione.

Invece Ŝ cos’è? Sicuramente un operatore, ma è di proiezione? No. Tuttavia si ha:

Ŝ | +ñ = S₁ | +ñ Ŝ | -ñ = S₂ | -ñ

cioè Ŝ è quell’operatore che applicato ad un autostato ci dà l’autostato ed il suo autovalore!

Esso è detto operatore autoaggiunto e nel nostro formalismo esso descrive le grandezze fisiche.

Quindi in questo apparato la grandezza fisica è descritta dalla somma di tutte le sue possibili determinazioni sperimentali (cioè da tutte le possibili misurazioni che di essa è possibile effettuare) moltiplicate per l’ente che rappresenta l’apparato sperimentale atte a determinarle (cioè l’operatore di proiezione, ovvero il preparatore di stato)!

Ricapitolando, lo spazio degli stati è caratterizzato dalle seguenti proprietà:

• è un insieme infinito di elementi. Infinito perché basta un certo numero di vettori e poi tutti gli altri vettori che si ottengono da quelli combinandoli in maniera opportuna sono sempre vettori dello stesso spazio;

• In esso è definito appunto il prodotto fra vettori e numeri (il cui risultato è sempre un vettore; esso è detto prodotto per scalare), fra vettori e vettori (prodotto il cui risultato è un numero, esso è detto prodotto scalare) e la somma fra vettori e vettori che dà vettori distinti (cioè con diversa lunghezza e direzione);

• Due stati il cui prodotto scalare è zero sono due autostati;

• Individuati tutti i possibili autostati essi sono la base dello spazio ed il loro numero dà la dimensione dello spazio;

• Il generico vettore di tale spazio si può sempre scrivere come una somma di tali autostati moltiplicati per opportuni coefficienti;

• In questo insieme possono agire degli operatori cioè degli enti che applicati a vettori danno altri vettori;

• Se l’operatore che agisce su di un autostato dà l’autostato ed il suo autovalore, esso è detto autoaggiunto;

• Se l’operatore che agisce sul generico stato dà un autostato al più moltiplicato per un coefficiente, esso viene detto operatore di proiezione;

• Se lo spazio degli stati ha dimensione infinita (cioè ammette un numero infinito di autostati) esso è detto uno spazio di Hilbert.

La connessione con la fisica è la seguente:

• Ad ogni autovalore corrisponde il risultato di una misura;

• Ad ogni operatore di proiezione corrisponde un determinato preparatore di stato;

• Ad un operatore autoaggiunto corrisponde un grandezza fisica, perché essa altro non è che la somma di tutti gli autovalori (cioè di tutti i possibili risultati della misura) che moltiplicano i loro rispettivi operatori di proiezione (cioè i loro corrispondenti preparatori di stato);

• Lo stato generico scritto come sovrapposizione di autostati obbedisce alla equazione di Schrödinger (questa è un’ipotesi esterna!): dove Ĥ è l’energia del sistema interessato;

• Le costanti c_i sono delle costanti il cui modulo al quadrato dà la probabilità che il sistema si trova nell’autostato iesimo

Questo è in sintesi il significato del formalismo della meccanica quantistica.

__________________

Note:

1) Per esempio basta consultare il famosissimo Landau-Lifsits “Meccanica” della Editori Riuniti. TORNA

2) Una derivazione “molto fondamentale” si può trovare nel lavoro di Soldano “Gravitational binding mass non-equivalence and foundations of physics” Int. J. Fusion Energ. vol. 3 July 1985; oppure è sufficiente consultare il libro del compianto prof. Salvatore Notarrigo, Alice nel mondo della realtà, che si può liberamente consultare nella bilbioteca del dipartimento di fisica dell’Università di Catania. TORNA

3) W.F. Edwards, Phys. Rev. Lett. Vol. 47 no 26 p. 1863, 1981 TORNA