Le basi
della Fisica
Giuseppe Garozzo
L’evoluzione della fisica del ‘900 ha dato adito a tutta
una serie di interpretazioni e discussioni che oggigiorno riempiono i testi di
filosofia della fisica. In questo scritto noi ci allontaneremo di molto dalle tematiche
trattate nei più comuni testi dedicati alle questioni epistemologiche in quanto
riteniamo che il dibattito attuale sia inutile e, sopratutto, senza via di
sbocco. Quindi problemi quali il ruolo
dell’ossservatore in meccanica quantistica o il concetto di tempo nella meccanica relativistica per noi non sono
i veri problemi da affrontare. Infatti, al fine di fare chiarezza sulla fisica
moderna, riteniamo che il problema base su cui spendere le nostre fatiche sia
il seguente: cosa sono le grandezze fisiche nella meccanica quantistica e nella
relatività? Alcuni concetti di tipo filosofico saranno indispensabili per la
trattazione seguente, e pertanto cercheremo di illustrarli brevemente.
1-
Concetti filosofici utili
Tra i molti concetti dell’armamentario filosofico, quelli
che riteniamo indispensabili per la nostra disamina sono i seguenti: reale, concreto e sensibile. Illustreremo adesso i significati di tali termini con
degli esempi. Dire che il sottoscritto Giuseppe
Garozzo é un individuo o entità sensibile significa
che lo si può incontrare per strada, stringergli la mano e fargli gli auguri
di Natale. Ovviamente tutte queste cose non si possono fare con l’individuo uomo ragno. Si osservi pure che anche
l’individuo o entità Pitagora è
sensibile, dato che in un determinato tempo c’è chi lo ha incontrato per strada
e gli ha fatto gli auguri di buon compleanno (ovviamente il Natale non esisteva
a quel tempo).
Torniamo adesso all’individuo uomo ragno. Esso non è sensibile,
tuttavia è concreto. Infatti uomo ragno è qualsiasi uomo che ha le
stesse capacità dei ragni, e cioè sa arrampicarsi sui muri, può fare grandi
salti, può produrre la ragnatela e può sollevare pesi dell’ordine di cinque
volte il proprio peso corporeo senza problemi. In definitiva cosa sia un uomo ragno è cosa ben definita. Quindi
uomo ragno è un individuo concreto ma,
ovviamente, non sensibile.
Adesso facciamo un salto nella teoria delle mutazioni
genetiche e cerchiamo di capire se una particolare mutazione del DNA può dotare
una persona degli stessi ‘poteri’ che hanno i ragni. Ebbene secondo la
Fisiologia umana e la Genetica è impossibile che un un’appartenente alla specie
umana possa per una qualche mutazione genetica acquistare le stesse capacità
dei ragni. Pertanto concludiamo che secondo la Genetica e la Fisiologia
l’individuo uomo ragno non è reale.
Quindi riassumendo l’individuo (o entità) uomo ragno è concreto ma non e sensibile nè
reale. Stressiamo ancora il concetto
di reale, affinchè il lettore non
creda che un individuo reale sia
necessariamente sensibile. Infatti il
concetto di reale è
sempre legato ad una teoria, cioè un individuo è reale se e solo se esiste in una teoria cioè se e solo se è
compatibile logicamente con una teoria. Facciamo un esempio. Consideriamo il concetto
di punto materiale. Ovviamente
l’entità punto materiale non è sensibile; tuttavia è concreta. Infatti
per punto materiale si intende un
corpo privo di estensione. Esso poi nella meccanica razionale acquista
l’attributo di reale. Infatti nella
Meccanica Razionale l’individuo punto
materiale è dotato di tutta una serie di proprietà
compatibili logicamente fra loro e con la stessa definizione di punto
materiale. Ma al di fuori della Meccanica Razionale l’entità (o individuo) punto materiale risulta solo concreto e non sensibile. Consideriamo adesso le luci di Hessdalen, un fenomeno
luminoso che si manifesta nella valle di Hessdalen in Norvegia. Tale fenomeno
luminoso è simile ai fulmini globulari ma presenta caratteristiche peculiari. Ovviamente
le luci di Hessdelen sono sensibili dal
momento che vengono viste, fotografate e monitorate con tutta una serie di
strumentazione. Esse sono pure concrete, dato
che per luci di Hessdalen si intendono tutta una serie di fenomoni luminosi con
particolari proprietà. Tuttavia esse non sono reali pcrchè non esiste ancora una teoria che possa giustificare
quella fenomenologia.
Infine portiamo un
esempio di un’entità non sensibile, non
concreta e dunque non reale: l’apeiron
di Anassimenc. Infatti per apeiron s’intende qualcosa di indefinito che
pervade tutto l’universo. Ma ovviamente la definizione ‘qualcosa di indefinito’
è auto contraddittoria dal momento che definiamo un qualcosa dando l’attributo di indefnito.
Pertanto essa risulta non sensibile (infatti nessumo ha mai visto
l’indefinito) e non concreta. Infine, essendo non concreta risulta non reale.
2- Le grandezze fisiche in meccanica classica
Come abbiamo già detto il confronto fra
teorie diverse è possibile effettuarlo se e
solo se si chiarisce cosa sia, in una data teoria, una grandezza fisica. Infatti ogni teoria fisica usa il termine grandezza fisica, ma ognuna con una
particolare accezione. Noi dimostreremo come la confusione attuale sulla
fisica moderna sia in pratica dovuta essenzialmente ad una confusione sul
concetto di grandezza fisica. Cominciamo
a porci la seguente domanda: che cos’è una grandezza fisica nella meccanica
classica?
A tale
quesito risponderemo fornendo il paradigma di grandezza fisica utilizzato nella
fisica di Newton.
Il
paradigma della grandezza fisica in meccanica classica è quello della misura di
una lunghezza. Per misurare una lunghezza banalmente si sceglie una sbarra presa
arbitrariamente come unità di misura (indichiamola con u e chiamiamola metro) e qualsiasi altro oggetto viene
poi misurato per confronto diretto. Dire per esempio che una data sbarra misura
3 metri significa che essa contiene tre volte il nostro campione di lunghezza,
scriveremo pertanto:
1 = 3 u
dove
con l si è indicata la lunghezza della
sbarra ovvero il concetto di lunghezza della sbarra. Ebbene l è il paradigma di grandezza fisica.
Ovviamente
nel fare la misura, conveniamo che nel trasporto il campione non si deformi,
che l’unità di misura sia una sbarra perfettamente diritta, che non commettiamo
errori nel segnare le tacche e così via. Nel caso poi che il nostro campione
non sia contenuto un numero intero di volte si esegue la decomposizione in
decimali, poi in centesimi, millesimi e così via. In questo paradigma possiamo
affermare che in genere la lunghezza di una sbarra l e’ sempre possibile scriverla come:
l = l u
dove l
è un numero (nell’esempio di sopra l = 3). Precisiamo ulteriormente la
simbologia introdotta. Con le lettere in grassetto, cioè nel nostro esempio con
l, indichiamo il concetto di lunghezza e più in generale la grandezza
fisica; con l indichiamo il numero associato alla grandezza fisica e
cioè il risultato della misura, e con u la grandezza fisica
fondamentale cioè la grandezza fisica associata alla sbarra scelta come unità
di misura.
Quindi 1,
u devono intendersi come entità concrete
ma non sensibili.
Ma
quando noi eseguiamo una misura col metro di un dato oggetto sensibile e scriviamo
1 = 3 u
l ed u sono sensibili o no? La risposta è sempre no!
Infatti le stesse assunzioni più o meno nascoste che si fanno per eseguire una
misura (ad esempio, campione perfettamente
diritto, e non deformabile) fanno si che u e dunque anche l rimangano sempre entità concrete ma non sensibili: infatti esse sono e rimangono concetti di lunghezza. In pratica quando noi eseguiamo una misura
facciamo sempre l’assunzione che il campione sia ‘perfctto’cioè operiamo sempre
col concetto di lunghezza del campione. L’unica
quantità che può essere sensibile è l. Infatti è su di essa che possiamo far
ricadere tutte le imperfezioni intrinseche del procedimento di misura. Non a
caso la misura di un oggetto sensibile viene espressa, ad esempio, nel seguente
modo:
l = (3±0.1) u
Ovvero il risultato,
sensibile, della misura l è sempre dato con un intervallo di incertezza.
All’interno poi della teoria della misura le entità l,u ed l risultano entità reali. Sintetizzando possiamo dire
che nella teoria della misura, che coincide con la teoria delle grandezze
fisiche sulla quale si fonda la meccanica classica, le grandezze fisiche del
tipo l ed u sono entità reali, concrete ma non sensibili, mentre per quanto riguarda il ruolo di l ce
ne occuperemo in seguito.
3- Gli spazi vettoriali della Meccanica Classica
Come il lettore ben saprà
la meccanica razionale fa uso delle seguenti entità: punti materiali, sbarre
perfettamente rigide, piani perfettamente lisci e così via. Tutte queste entità
ovviamente non sono sensibili; tuttavia
risultano concrete, e dato che fanno
parte di una teoria che stabilisce alcune assunzioni su di esse (ad esempio ne
stabilisce le leggi del moto) sono pure reali.
Ovviamente alla sbarra perfettamente rigida, così come al piano
perfettamente liscio, è possibile associare direttamente una grandezza fisica
(rispettivamente la lunghezza e l’area), mentre al punto materiale possiamo
solo associare indirettamente una data grandezza fisica (ad esempio lo spazio
percorso). Le entità fondamentali della meccanica classica a cui è possibile
associare direttamente una data grandezza fisica sono lo spazio, il tempo e la
massa. A parte la massa, lo spazio ed il tempo sono concetti dati come
primitivi. Come è noto le grandezze fisiche associate a tali entità sono
scalari e vettoriali. In particolare per il tempo e per la massa abbiamo
bisogno di eseguire solo un confronto diretto per effettuare la misura. Mentre
per lo spazio, ovvero per la lunghezza, in genere le cose sono un pò più
complicate. Infatti per misurare la lunghezza di una traiettoria non rettilinea
abbiamo bisogno di cambiare continuamente l’orientazione e verso del nostro
campione di misura. La stessa
cosa accade se vogliamo misurare la distanza di un dato corpo rispetto ad un
riferimento. In tal caso dalla geometria sappiamo che o assegniamo il valore
della lunghezza (cioè l) e
l’orientazione oppure assegniamo tre valori della lunghezza riportati lungo i
tre assi cartesiani. Conveniamo di indicare il numero associato ad una data
grandezza vettoriale con una segnatura sotto la lettera, ad esempio
l= (l1, l2,
l3)
In questo caso, dato che ![]() (e quindi l1, l2, l3)
rappresenta un risultato ideale di una data misurazione, esso non è sensibile ma solo reale e concreto. Indicati
poi con i, j e k le grandezze fisiche
campioni lungo i tre assi cartesiani si pone (per il teorema di Pitagora):
(e quindi l1, l2, l3)
rappresenta un risultato ideale di una data misurazione, esso non è sensibile ma solo reale e concreto. Indicati
poi con i, j e k le grandezze fisiche
campioni lungo i tre assi cartesiani si pone (per il teorema di Pitagora):
l = l1 i + l2
j + l3k (1.1)
dove con l
abbiamo indicato la grandezza fisica vettoriale. Ovviamente la (1.1) può
essere considerata come la definizione di combinazione lineare. L’insieme di
entità che si ottengono dalla (1.1) al variare dei numeri (reali) l1, l2, l3
è detto spazio vettoriale. Per
essere più precisi uno spazio vettoriale è un insieme di elementi detti
vettori in cui sono definiti una somma interna ed un prodotto scalare che
godono rispettivamente delle comuni proprietà della somma fra numeri reali per
quanto riguarda l’operazione di somma fra vettori, e della proprietà
associativa e distribuitiva ed esistenza dell’elemento neutro per quanto
riguarda il prodotto fra vettore e scalare. Ma ciò è ben noto al lettore:
quello che noi qui vogliamo sottolineare è che le grandezze fisiche in
meccanica classica sono dei vettori (le grandezze scalari sono vettori di
dimensione uno) e che le proprietà dei vettori sono desunte dalla definizione
operativa di grandezza fisica che abbiamo istituito per la meccanica classica.
Ribadiamo ancora che il paradigma di grandezza fisica dato è determinato
operativamente mediante la più semplice operazione fisica che conosciamo: il
confronto diretto. Infine il confronto con la misura sensibile si ottiene
mediante l che da oggetto concreto e
non sensibile diventa sensibile e quindi determinato con un margine di
incertezza.
4- Il sensibile e l’ideale in meccanica classica
Il lettore può rimanere confuso circa il ruolo da
attribuire ad l (o l nel caso di
numero associato ad una grandezza vettoriale avente più di una dimensione).
Premettiamo che per semplicità di trattazione indicheremo con
l’attributo di ideale ciò che non è sensibile ma che risulta concreto (e può pure essere reale). Supponiamo di volere affrontare
il seguente problema: determinare la
traiettoria di un grave lanciato orizzontalenitente con una data velocita’
iniziale trascurando l’attrito dell’aria.
Innanzitutto facciamo l’assunzione che il grave sia modellizzabile con
un punto di materiale avente una massa m (ovviamente gli oggetti con cui
lavoriamo sono le grandezze fisiche) e sia r(t) la sua
traiettoria. In questo stadio dell’analisi possiamo benissimo passare dalle
grandenzze fisiche ai numeri ideali ad essi associati: tali numeri sono ideali
perchè possiamo pensare di associarli mediante una misurazione perfetta cosa
che da un punto di vista ideale è sempre possibile fare. Pertanto possiamo supporre
di avere un punto materiale di massa m e
di traiettoria r(t)=(x(t),y(t)) data
da (per le leggi di Newton):
x(t)=v0 t + x0
y(t) = 1/2 gt2+y0
dove v0
è la velocità (orizzontale) iniziale ed x0 e
y0 la posizione iniziale del punto. Alla fine si
ottiene che la traittoria è una parabola.
Come si vede da questo esempio finchè ci
limitiamo alla trattazione ideale dei sistemi fisici possiamo benissimo passare
tranquillamente dalle grandezze fisiche ai numeri ad essi associati. Ovvero in
questo stadio di trattazione c’è una corrispondenza biunivoca fra entità,
grandezze fisiche associate e numeri ad essi associati.
Le cose cambiano quando ad esempio vogliamo
empiricamente verificare le formule di sopra. In questo caso le x(t) e y(t) cessano di essere quantità ideali
e diventano sensibili. Tuttavia tale passaggio non è banale perchè richiede una
teoria dell’esperimento con connessa analisi degli errori. D’ora in avanti
indicheremo con <l> i numeri sensibili associati alle
grandezze fisiche: nel caso del grave avremo <x(t)> e <y(t)>.
Riassumendo possiamo affermare che nella
relazione:
l = l u
tutte e tre le entità sono reali concrete ed
ideali cioè non sensibili; tuttavia la l può diventare sensibile e pertanto
qualora nella relazione di sopra sostituiamo al numero l ottenuto con una misura ideale quello ottenuto con una misura
sensibile si ha:
l = <l>
u
Ovviamente la meccanica classica tratta solo
delle grandezze fisiche e dei valori ideali. Pertanto, ripetiamo, il confronto
col dato empirico richiede una non banale elaborazione mediante la teoria della
misura, dei valori ideali e/o una buona preparazione dell’esperimento al fine
da riprodurre nel miglior modo possibile le condizioni ideali (ad esempio il
piano inclinato è un buon espediente per simulare condizioni quasi ideali per
la caduta dei gravi).
5- La teoria
della misura
Misurare significa fare interagire l’oggetto
della misura con un altro oggetto detto apparato di misura. Nella meccanica
classica entrambe cose sono in linea di principio descrivibili mediante i suoi
principi e le sue leggi del moto. In genere la determinazione sperimentale
delle grandezze fisiche (cioè di <l>)
richiede una particolare costruzione dell’apparato di misura ed una
particolare costruzione dell’esperimento. Da quanto detto si evince come misurare non sia una cosa banale. Nella
fisica di Newton, di Galileo e di Archimede si era soliti parlare di operazioni
fisiche elementari, per indicare le più semplici operazioni fisiche di misura
che si possono pensare ed effettuare. Ovviamente, come già detto, la più
semplice operazione fisica di misura è quella di confornto diretto. Infatti non
esiste un’operazione fisica più semplice di questa. Tuttavia il lettore osservi
che, per quanto semplice, essa nasconde molte assunzioni semplificative
(trasporto rigido ad esempio). Però senza queste assunzioni implicite non è
possibile fare nulla, infatti che senso avrebbe misurare con una sbarra
deformabile?
Ribaditi questi concetti, fermiamoci a
parlare brevemente della determinazione sensibile delle grandezze fisiche.
Ogni apparato di misura ha ovviamente un
tempo morto, una precisione finita ed è soggetto alle interferenze
dell’ambiente per quanto accuratamente noi possiamo preparare l’esperimento.
Per tale ragione si usa dire che uno strumento di misura è in grado di fornirci
solo il valore medio (mediato al limite solo nel tempo) di una data grandezza
fisica l (non importa se è un
vettore unidimensionale o tridimensionale). Pertanto indicato con l(t) i valori ideali che essa può
assumere e con f(t) la distribuzione di probabilità dei valori di l
nel tempo, la determinazione sensibile di l sarà:
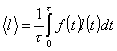 (1.2)
(1.2)
dove τ è il tempo morto dello strumento
di misura. In generale la distribuzione di probabilità non è nota. Essa può
essere stimata a partire da un determinato modello dell’esperimento. Il caso
ideale si ottiene per f(t)=1. Nel
caso poi in cui noi supponiamo che la grandezza l non sia soggetta a
fluttuazioni dovute alle interferenze dell’ambiente circostante (cosa che
abbiamo modellizzato con l’introduzione della funzione di distribuzione f(t)),
per l’inevitabile esistenza del tempo morto dello strumento si ha:
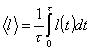 (1.3)
(1.3)
Dalla (1.2)o dalla sua versione semplificata (1.3) segue
che in generale:
![]() (1.4)
(1.4)
Per convincerci
della validità generale della (1.4) il lettore può fare l’esercizio di
applicare la (1.3) nel caso dell’oscillatore armonico unidimensionale dove il
valore ideale della grandezza fisica spostamento è dato dalla seguente
espressione:
l(t) = A sin ωt.
Infine vogliamo segnalare come la (1.4) e’ un
caso particolare della relazione più generale:
![]() (1.5)
(1.5)
dove l e m sono due grandezze fisiche arbitrarie (non importa se di
dimensione uno, due o tre).
6- Manipolazione delle grandezze fisiche in meccanica classica
Adesso il lettore per potere proseguire oltre
è bene che si ricordi la differenza fra determinazione ideale e determinazione
sensibile di una grandezza fisica. Infatti mentre le grandezze fisiche e la
loro determinazione ideale in meccanica classica fanno parte di uno spazio
vettoriale e quindi, verficano ad esempio la proprietà associativa, e cioè
(l × m) = (l) × (m)
e quindi possono essere trattate come numeri,
le loro determinazioni sensibili non la verificano!1 Infatti le loro
determinazioni sensibili verificano la (1.5). Tuttavia per quanto riguarda le
altre proprietà le determinazioni sensibili hanno lo stesso comportamento di
quelle ideali. In sintesi possiamo affermare che mentre le grandezze fisiche e
le loro determinazioni ideali verificano un’algebra associativa per quanto
riguarda il prodotto, le determinazioni sensibili verificano un’algebra, in
generale, non associativa e pertanto non possono essere trattate come numeri.1 Purtroppo noi non abbiamo dimestichezza con entità
che verificano un’algebra non associativa per quanto riguarda l’operazione di
prodotto. Tuttavia è possibile mostrare che si può passare da un’algebra (in
generale) non associativa ad una associativa ma non commutaiva, a noi
sicuramente più familiare. Vediamo come. Siano ![]() e
e ![]() due elementi di un algebra non associativa rispetto al
prodotto, ovvero
due elementi di un algebra non associativa rispetto al
prodotto, ovvero
![]()
Indichiamo con ![]() e
e ![]() due operatori che
agiscono su vettori (appartenti ad uno spazio vettoriale dotato di prodotto
scalare). Associamo a questi operatori gli elementi dell’algebra non
associativa mediante la seguente corrispondenza:
due operatori che
agiscono su vettori (appartenti ad uno spazio vettoriale dotato di prodotto
scalare). Associamo a questi operatori gli elementi dell’algebra non
associativa mediante la seguente corrispondenza:
![]()
In pratica la corrispondenza viene istituita
associando ad ogni elemento dell’algebra non associativa un operatore di cui
esso sia un autovalore. Stabiliamo ora che all’elemento ![]() venga associato
l’operatore
venga associato
l’operatore ![]() (dove il puntino indica una data
operazione di prodotto fra operatori) che per semplicità di scrittura
scriveremo
(dove il puntino indica una data
operazione di prodotto fra operatori) che per semplicità di scrittura
scriveremo ![]() . Quindi
. Quindi
![]() (1.6)
(1.6)
Ora se ![]() fosse un autovettore sia di
fosse un autovettore sia di ![]() che di
che di ![]() si avrebbe:
si avrebbe:
![]()
dove è stato assunto che gli elementi
dell’algebra non associativa commutano con gli operatori. Allora per la
supposta proprietà commutativa degli elementi ![]() e
e ![]() segue che,
nell’ipotesi in cui
segue che,
nell’ipotesi in cui ![]() è un autovettore sia
di
è un autovettore sia
di ![]() che di
che di ![]() :
:
![]() (1.7)
(1.7)
Dalla (1.6) e (1.7) segue che:
![]()
ma ciò è assurdo.
L’assurdo nasce proprio dall’ipotesi che ![]() è un autovettore sia di
è un autovettore sia di ![]() che di
che di ![]() ovvero che
ovvero che ![]() e
e ![]() posseggano un autovettore comune.
posseggano un autovettore comune.
Quindi affinchè si possa istituire una
corrispondenza biunivoca fra elementi di un’algebra non associativa (rispetto
al prodotto) ed operatori di cui essi siano gli autovalori è necessario che in
genere tali operatori non posseggano autovettori in comune, ovvero, che in
genere, essi non commutino. Infatti come si può leggere nei testi base di
algebra lineare due operatori che commutano hanno autovettori in comune e
viceversa (si potrebbe passare ad operatori, detti superoperatori, in cui
questa proprietà non risulta verificata, ma per ora questo esula dalle nostre
intenzioni).
Concludiamo questo paragrafo osservando che
la corrispondenza fra elementi dell’algebra non associativa ed operatori
appartenenti ad un algebra non commutativa è biunivoca se e solo se si
stabilisce che
![]()
dal momento che un operatore commuta sempre
con una sua potenza, il che significa, nella teoria delle grandezze, che ![]() . Per ora ci basta sottolineare che è possibile descrivere le
determinazioni sensibili con un’algebra non commutativa anche se con alcune importanti
prescrizioni.
. Per ora ci basta sottolineare che è possibile descrivere le
determinazioni sensibili con un’algebra non commutativa anche se con alcune importanti
prescrizioni.
7- Un esempio concreto: l’oscillatore armonico
Adesso vediamo di fare un esempio al fine di
rendere più chiaro quanto esposto fino a questo momento. A tal proposito
consideriamo il sistema ideale costitutito dall’oscillatore armonico.
L’equazione del moto ideale (cioè che lega le grandezze fisiche ideali) è la
seguente:
![]()
dove x è lo spostamento, m la
massa del punto materiale e k la
costante elastica. Posto
![]()
la soluzione dell’equazione del moto
soddisfacente la condizione iniziale x(0) = 0 è la seguente:
x(t) = A sen ω t
A
è una costante e rappresenta l’elongazione massima della molla. Ovviamente la
velocità è data dalla seguente espressione:
![]()
pertanto l’impulso (cioè la quantità di moto
indicata con p)
è data dalla:
![]() .
.
Siamo in grado adesso di calcolarci alcune
quantità. Detto allora τ il tempo morto di uno strumento di misura della
posizione e dell’impulso, si ha:
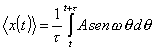 onde
onde
![]()
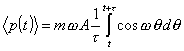 onde
onde
![]()
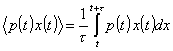 onde
onde
![]()
Si osservi come:
![]() (1.8)
(1.8)
Invece
è possibile dimostrare che la legge di Newton è ancora valida ovvero che:
![]() (1.9)
(1.9)
Da
essa segue che l’energia media così calcolata:
![]() (1.10)
(1.10)
si conserva (infatti basta derivare rispetto al tempo la (1.10)). In questo caso l’energia media è data dalla seguente espressione:
![]()
Si osservi come al limite per τ che
tende a zero le grandezze medie corrispondano a quelle ideali e la (1.8) cessa
di essere valida. Infine per concludere vogliamo stressare sul fatto che la
(1.8), cioè la validità di un’algebra non associativa, esprime il fatto che le
grandezze fisiche x(t) e p(t) non sono statisticamente
indipendenti.
Conclusioni
Da quanto detto si evince che prima di
affrontare qualsiasi analisi di una data teoria occorre fare una disanima di
quale sia la natura delle grandezze fisiche di cui essa tratta. Infatti, come
abbiamo dimostrato nell’ambito della meccanica classica, vi è una netta
differenza fra le relazioni (cioè equazioni) che intercorrono fra entità ideali
e fra entità sensibili. Le prime obbediscono alla comune algebra dei numeri
ordinari, i secondi, invece, ad un’algebra non associativa e/o equivalentemente
ad un’algebra non commutativa rispetto al prodotto. Riteniamo pertanto che queste
importanti conclusioni siano propedeutiche per una analisi critica della
meccanica quantistica. Come infatti è noto, in tale teoria le grandezze
fisiche sono descritte da quantità che obbediscono ad un’algebra non
commutativa. Pertanto il problema che affronteremo in un prossimo scritto, alla
luce di quanto detto, è il seguente: possono essere interpretate le grandezze
fisiche della meccanica quantistica come medie statistiche di grandezze
‘classiche’? Ebbene una parziale risposta è già possibile darla ed è,
ovviamente, affermativa dato che abbiamo mostrato come sia possibile
rappresentare con un’algebra non commutativa le determinazioni sensibili di
grandezze classiche.
_____________
Note
1 Per il momento non vogliamo eccedere con il rigore matematico.
Sottolineamo che tale asserto nasce da un teorema noto come teorema di
Gleason. TORNA