REALE E
APPARENTE:
LE
TRASFORMAZIONI DI
LORENTZ E IL
CONCETTO DI VELOCITA’
Pietro Di Mauro
Abstract
In special relativity two reference frames that move wìth unifom
velocity relative ν known are considered. How can we define and measure
it since the measure of the space and time are dependent on it? The “classic”
definition of velocity is the so-called Galilean transformation. By utilizing a
signal of light an observer can find the velocity of a body (or a system)
compared to him. And every observer can do this. This way it is possible to
obtain a formula that let us find the velocity (that result always minor c)
and the position of a body in each instant. It is possihle, for example, to
measure also the length of a rod (indirect way) always finding the same length.
In the Appendix is reported the introduction to a communication given to the
LXXXI S.I.F. Congress on the “real” and “apparent” and the Lorentz
transformation.
In tutti i discorsi che si
fanno sulla relatività ristretta si suppone sempre che ci siano due sistemi di
riferimento (due osservatori) in moto relativo traslatorio uniforme tra loro
con velocità v, e questa si suppone
nota.
Già Einstein nel suo lavoro
deI 1905 scrive: “... Immaginiamo ora
l’asta collocata lungo l’asse X del
sistema di coordinate stazionario, e che ad essa venga impresso un moto
traslatorio uniforme (con velocità v) parallelamente all’asse X nel verso delle
x crescenti”. E dopo: “… Imprimiamo
ora all’origine di uno dei due sistemi, che chiameremo k, un moto con velocità
(costante) v nella direzione delle x crescenti dell’altro sistema (K), che
rimane a riposo, e supponiamo che tale velocità sia comunicata agli assi
coordinati del sistema k, al relativo regolo e agli orologi”.1
Com’è possibile conoscere la
velocità v relativa di un osservatore
rispetto all’altro? Com’è possibile definirla?
In relatività sembrerebbe
che la velocità sia definita nel modo usuale, come rapporto tra spazio percorso
e tempo impiegato a percorrerlo. Ma se spazio e tempo sono “relativi”,
dipendono dalla velocità, non ci troviamo forse in un circolo vizioso?
Nella meccanica di Galilei e
Newton la velocità di un corpo (o, nella meccanica di Eulero e Lagrange, di un
sistema) rispetto ad un osservatore (o un altro sistema) viene definita come
ricordato prima.
Scrive Galilei: “Diamo avvio a una nuovissima scienza
intorno a un soggetto antichissimo. Nulla v’è, forse, in natura, di più antico
del moto, e su di esso ci sono non pochi volumi, né di piccola mole, scritti dai filosofi; tuttavia tra le sue
proprietà ne trova molte che, pur degne di essere conosciute, non sono mai
state finora osservate, nonché dimostrate… Del moto equabile: Circa il
moto equabile o uniforme ci occorre una sola definizione, che formulo così: Definizione:
Moto uguale o uniforme intendo quello in cui gli spazi percorsi da un mobile in
tempi uguali, comunque presi, risultano tra di loro uguali”.2
In un’altra sua opera Galilei
aveva trattato il concetto di velocità, in un dialogo tra Salviati (Galilei),
Simplicio e Sagredo:
“Sal.
Credo che voi mi burliate, fingendo di non capire quel che voi intendete meglio
di me. Però ditemi, signor Simplicio: quando voi v’immaginate un mobile esser
più veloce d’un altro, che concetto vi figurate voi nella mente?
Simpl. Figuromi, l’uno passar nell’istesso tempo maggiore spazio dell’altro,
o vero passare spazio uguale, ma in minor tempo.
Sal. Benissimo: e per mobili egualmente veloci, che concetto vi figurate?
Simpl. Figuromi che passino spazi eguali in tempi eguali.
Sal. E non altro concetto che questo?
Simpl. Questo mi par che sia la propria definizione de’ moti eguali.
Sagr. Aggiunghiamoci pure quest’altra di più: cioè chiamarsi ancora le
velocità esser eguali, quando gli spazi
passati hanno la medesima proporzione che i tempi ne’ i quali sono passati, e
sarà definizione più universale.
Sal. Così è, perché comprende gli spazi eguali passati in tempi ineguali, ma
proporzionali a essi spazi”.3
E infine formalizza il
concetto di velocità in relazione ai concetti di spazio e tempo con le seguenti
proposizioni:
“Teorema I.
Proposizione I: Se un mobile dotato di moto equabile, percorre due spazi
con una stessa velocità, i tempi dei moti staranno tra di loro come gli spazi
percorsi.
Teorema II
Proposizione II: Se un mobile percorre due
spazi in tempi uguali, quegli spazi staranno tra loro come le velocità. E se
gli spazi stanno tra loro come le velocità, i tempi saranno uguali.
Teorema III.
Proposizione III: Se il medesimo spazio
viene percorso con velocità diseguali, i tempi dei moti rispondono
contrariamente alle velocità”.4
Dunque, come postula anche
Bridgman: “Il concetto di velocità, come
definito di solito, implica i due
concetti di spazio e tempo. Le operazioni con cui noi misuriamo la velocità di
un oggetto sono queste: dapprima osserviamo l’istante in cui l’oggetto è in una
posizione, poi osserviamo l’istante in cui esso si trova in un’altra posizione,
dividiamo la distanza fra le due posizioni per l’intervallo di tempo e se
necessario, quando la velocità è variabile, passiamo al limite” (e qualche
rigo più avanti, Bridgman inserisce la seguente nota: “E’ una questione interessante per lo psicologo se il concetto di
velocità non è qualcosa di più primitivo, nell’ordine dell’apprendimento, che
non quello di tempo, e se il concetto di tempo non deriva dall’osservare le
cose in moto, o se in effetti non vi è nessuna connessione necessaria tra la
velocità e il tempo in termini di esperienza non elaborata”).5
Quindi, per definizione, la
velocità media di un corpo (un punto materiale, nel senso euclideo),
trascurando, come si fa sempre, la sua massa, o di un sistema ad esso associato
che si muove dal punto 1 al punto 2, rispetto ad un osservatore, è:
essendo x(t1)
la posizione del corpo all’istante t1
e x(t2) la
posizione del corpo all’istante t2 rispetto
all’osservatore, e i tempi misurati con un orologio dell’osservatore.6
Dato che in questo scritto
(come nella relatività ristretta) si trattano velocità costanti nel tempo,
possiamo sempre utilizzare la 1), senza passare al limite, per scrivere la
velocità del corpo (o del sistema ad esso associato).
Questo stesso concetto di
velocità è quello utilizzato in geometria. Scrive Peano:
“Noi vediamo,
nel mondo fisico, dei corpi rigidi muoversi col variare del tempo. Possiamo
studiare la successione delle infinite posizioni che assume il corpo; ovvero
possiamo limitarci ad esaminare i rapporti fra due posizioni della figura, la
prima e l’ultima, senza occuparci delle posizioni intermedie assunte dal corpo
nel passare dall’una all’altra. Questo solo studio particolare è fatto da
Euclide, e si può considerare come studio geometrico. Il primo studio, più
generale e molto più complicato, fa
parte della Cinematica, e si può escludere dalla Geometria. Quindi mi
pare conveniente di escludere da un libro di geometria elementare le seguenti
proposizioni e simili: «Un punto muovendosi descrive una linea». «Un punto che
percorre la retta, non può passare dall’una banda all’opposta di un punto fisso
m di questa retta senza coincidere una volta con esso». Mettendoci adunque dal
primo punto di vista, se m è un moto, ed a è un punto fisso dello spazio,
risulta determinato un nuovo punto che indicheremo con ma, e che si chiama «la
nuova posizione che ha il punto a dopo il moto m». Quindi il moto è una
trasformazione di punti in punti”.7
E successivamente ribadisce
la convenzione, quando tratta del rapporto tra grandezze eterogenee, che la velocità
= spazio/tempo = quantità di c (centimetri)
/ quantità di s (secondi) e, per
esempio, si ha che la velocità della luce = c=
3 x 1010c/s .8
La 1) è possibile scriverla
nella forma:
2) x(t2)=x(t1)+v(t2 - t1)
In quest’ultima equazione è
possibile sostituire x’(t1) al
posto di x(t1 ), cioè la
posizione iniziale considerata in un altro sistema di riferimento in moto (con
velocità v) rispetto al sistema
dell’osservatore, in generale dovrebbe essere x(t1) = a + x’(t1), essendo a = OO’
= distanza tra le due origini dei sistemi di riferimento. Ma a partire da
Einstein9 si fa la convenzione
che nell’istante iniziale delle osservazioni (t1 nel nostro caso) le due origini coincidano, cioè a = O.
E d’altra parte è sempre
possibile considerare la posizione iniziale del corpo, nel punto 1, all’istante
iniziale, come l’origine di un altro sistema di riferimento (e di un
possibile altro osservatore) dotato anch’esso di orologio che segna lo
stesso tempo dell’altro.
Con la sostituzione operata
si ottengono:
che,
a partire da P. Franck (1909), viene chiamata trasformazione di Galilei.
Dunque, le cosiddetta trasformazione
di Galilei (chiaramente non si trova negli scritti di Galilei!) è
tautologicamente equivalente alla definizione data di velocità: la trasformazione
di Galilei è la definizione classica di velocità!
Ma la trasformazione di
Galilei è stata sostituita dalle più corrette (?!) e più generali (?!) trasformazioni di Lorentz! Anche
contro il parere di Einstein, che nel 1934 scriveva: “Se una sola delle sue [della teoria della relatività] conseguenze apparisse inesatta, bisognerebbe
abbandonarla: ogni cambiamento sarebbe impossibile senza scuotere tutto
l’edificio. Ma nessuno deve pensare che
la grande creazione di Newton
possa realmente essere sostituita da questa teoria o da una consimile. Le sue
idee grandi e chiare conserveranno sempre in avvenire la loro importanza
eminente, ed è su di esse che fondiamo ogni speculazione moderna sulla natura
dei mondo”.10
E la definizione di velocità? Usualmente in
tutte le derivazioni delle trasformazioni di Lorentz si considera v
nota e definita classicamente (v =x/t).11 Ma dalle trasformazioni di Lorentz, a
differenza di quelle di Galilei, la velocità cosi definita si ricava solo
ponendo x(t1) = x’(t1)
= 0. Senza questa posizione
si ha, in generale, avendo indicato x = x(t2 ), x0 = x(t1
), Δt = t2 - t1 :
dalla quale si ricava 
(eliminando la
radice con il segno positivo) solo per 
Anche nella derivazione di altre
trasformazioni più generali o diverse da quelle di Lorentz la velocità si dà
sempre nota, anche se la sua definizione alla fine si può discostare da quella
usuale, pur restando una finzione dello spazio e del tempo.12
D’altra parte quando in una
qualunque trasformazione che riguarda, per esempio lo spazio (in funzione del
tempo e della velocità), si richiede l’omogeneità, con le convenzioni date, può
essere presente un termine che sia prodotto di funzioni solo del tempo e della
velocità, che abbiano le dimensioni di t e v, ma non è detto che debba essere il più semplice vt! Proprio la definizione di velocità si
potrebbe considerare come possibile discriminante tra le varie trasformazioni
trovate.
Nelle trasformazioni lineari
più generali possibili che lasciano invariate in forma le equazioni di Maxwell
e soddisfano i postulati della relatività ristretta di Einstein, da noi trovate
nel 199613, è proprio la
definizione di velocità ad operare la possibile distinzione tra le infinite
trasformazioni.
Infatti , si hanno le seguenti trasformazioni:
con a una qualunque funzione di v.
Con la solita imposizione di
x’ = 0 si ottiene:
Se consideriamo x/t = v si otterrà per la a il
termine 
e dunque le trasformazioni di Lorentz come scritte
usualmente. Ma se fosse, per esempio, 
si otterrebbe per a
il termine 
e dunque altre trasformazioni
che soddisfano sia i postulati di Einstein che l’invarianza in forma delle
equazioni di Maxwell! In generale se x/t = φ(v)
si ottiene per a il termine 
tale da individuare
infinite trasformazioni ugualmente rispondenti alle ipotesi fatte e dipendenti
solo dalla definizione di velocità.
Com’è possibile definire e
misurare la velocità di un corpo (o di un sistema) rispetto ad un osservatore O, in modo indiretto, utilizzando i
segnali luminosi perconoscere la posizione di un corpo nel tempo (supponendo
la coincidenza tra spazio ottico e tattile evidenziata da Bridgman), mantenendo
la definizione usuale di velocità (spazio percorso/tempo impiegato a
percorrerlo)?14
In modo più semplice, ma senza
perdere di generalità, è possibile trattare la questione in una sola
dimensione, x. La posizione di un corpo, al tempo t, rispetto
all’osservatore O dotato di orologio,
può essere trovata in questo modo).15
Al tempo τ1
lancia un raggio di luce verso il corpo. Viene riflesso dal corpo e
ritorna all’istante t1. Il corpo all’istante t1 si
trova nella posizione:
essendo
± ε1 lo spazio percorso dal corpo nel tempo che impiega la
luce per tornare dopo la riflessione sul corpo che si allontana o che sì
avvicina all’osservatore, avendo tenuto conto che il tempo t, istante in
cui il raggio raggiunge il corpo, è dato da 
e, quindi, che la luce
impieghi lo stesso tempo nell’andata e nel ritorno (quest’ultima viene da
alcuni chiamata “tesi di convenzionalità”16).
Analogamente scegliendo
arbitrariamente un altro istante τ 2 si ha:
La velocità media che
l’osservatore assegnerà al como sarà data dalla 1) sostituendo la 7) e la 8).
Si ottiene:
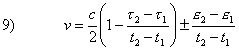
Ma si avranno anche:
e
sostituendo si ottiene la formula cercata:
avendo posto 
e 
.
La 11), dunque, ci permette
di calcolare le velocità di un corpo (o di un sistema) rispetto ad un
osservatore in modo indiretto, dalla sola misura di tempi sull’orologio
dell’osservatore. La velocità v data dalla 11) sarà sempre minore di c, dato che, per come si è definita, si
avrà sempre τ2 > τ1 e t2 > t1 (oltre a t2 > τ 2 e t1
> τ 1).
Inoltre si troverà v > 0, cioè
il corpo si allontanerà dall’osservatore se t2 - τ 2 > t1 - τ 1 , mentre si troverà v < 0,
corpo in avvicinamento, nel caso contrario.
Ponendo T1 = t1 - τ 1 , T2 = t2 - τ 2 e ΔT = T2 - T1 la 11) si può scrivere:
dalla
quale si evince che v®0 per ΔT®0 e v®c per
ΔT®¥.
Data l’arbitrarietà degli istanti iniziali, sarà possibile scegliere,
per esempio, τ2 = t1 (cioè nell’istante in cui si riceve il ritorno del primo segnale
parte il secondo) e la 12) diventa la più semplice:
Utilizzando queste formule
della velocità è possibile conoscere in ogni istante la posizione del corpo
rispetto all’osservatore che ha misurato la velocità del corpo. Si ha, avendo
posto t2 = t, istante generico:
che con le convenzioni adottate all’inizio,
ci dà la posizione, istante per istante, in funzione del tempo e della
velocità, del corpo come misurata dall’osservatore. E’ la “trasformazione” per
le misure dello spazio!
Chiaramente le cose si
complicano sc si considera la velocità come vettore. In questo caso la 11)
diventa:
essendo 
e 
i due “vettori
velocità della luce” con moduli uguali ma versi e direzioni, in generale,
diversi; questa velocità andrebbe poi usata in tutte le formule e applicazioni.
Dunque, è possibile in modo
indiretto, utilizzando un segnale luminoso, conoscere la velocità di un corpo
e la sua posizione istante per istante rispetto a un osservatore mantenendo la
definizione di velocità usuale e trovando che questa deve essere sempre minore
della velocità della luce (come in relatività!). Questo è ciò che un osservatore
può dire del corpo dal punto di vista cinematico. La defnizione della grandezza
velocità è rimasta invariata, ma è cambiato il metodo per misurarla e con ciò,
forse, la sua misura. E’ la misura di una grandezza che può dipendere dal
metodo usato per misurarla non già la sua definizione! E non come afferma, per
esempio, Bondi e la fisica moderna tutta: “Una
qualsiasi quantità è definita dal metodo impiegato per misurarla”17(si fa notare il termine quantità e non grandezza!).
In relatività si considerano
però sempre due osservatori che descrivono lo stesso corpo e che dovrebbero
scambiarsi le conoscenze delle grandezze misurate da ciascuno. Questo è
richiesto: l’impossibile confronto tra osservazioni fatte di un evento (o di un
corpo, di un sistema) da due osservatori in moto tra loro18. E d’altra parte in tutti gli esperimenti che
vengono portati a supporto della teoria non ci sono mai due osservatori!
L’unico osservatore è colui che raccoglie le “sue” misure, che in questo senso
si possono considerare “assolute” (l’osservatore non potrà accorgersi di essere
in moto relativo uniforme rispetto a un altro, come chiarito da Galilei!).
Il discorso sulle possibili
trasformazioni da usare per passare da un sistema (osservatore) ad un altro
nasce dalla pretesa di dover confrontare le misure fatte da un osservatore O di un evento E e quelle fatte sullo stesso evento da un altro osservatore O’ (supposto in moto relativo uniforme
rispetto ad 0) e quindi conoscere,
per esempio, la posizione di E rispetto
a O’ come “vista” da O (o viceversa)19. Senza la pretesa del confronto ciascun osservatore
potrà fare le sue misure senza dover invocare nessuna trasformazione!
Supponiamo di avere i due
osservatori O e O’, in moto tra loro, muniti di orologi identici. Supponiamo, come
fanno tutti, a partire da Einstein (anche se nel suo lavoro del 1905 non lo
afferma esplicitamente), che gli orologi segnino lo stesso tempo
(sincronizzati) quando passano uno accanto all’altro. Quando O’ si troverà distante da O quest’ultimo per sapere il tempo
segnato dall’orologio di O’ lancia un
segnale all’istante t0 verso O’. Il segnale è ricevuto da O’
all’istante t riflesso verso O
e da questo ricevuto all’istante t1. Tutti, a cominciare
da Einstein, come si è detto prima, pongono20 :
(a partire da questa Einstein nel 1905 crede di derivare le uniche
trasformazioni possibili, cioè quelle di Lorentz!21).
La posizione di O’
assegnata da O all’istante t sarà:
(all’istante t1 sarà dato dalla 7)). Dalle 16) e 17) si
ottiene:
cioè il tempo segnato dall’orologio di O’ è lo stesso di quello segnato
dall’orologio di O, essendo x/c il tempo misurato da O perché il raggio di luce raggiunga O’. Se i due orologi, in un certo
istante hanno segnato lo stesso tempo (quando sono passati uno accanto
all’altro) continueranno a segnare lo stesso tempo, anche se sono separati da
una distanza x.
Lo stesso si può dire per la
lunghezza di un regolo.
Supponiamo che O conosca la lunghezza a riposo di
un’asta, con metodo diretto (per confronto con l’unità di misura) e questa
risulta AB = l0 (comprensiva dell’unitàdi misura). Si vuole
determinare la lunghezza dell’asta quando essa è in moto con velocità v, rispetto ad O, con metodo indiretto, mediante segnali luminosi come si è fatto
finora.
O lancia
un segnale verso B al tempo t0 e
uno verso A (l’estremità dell’asta più vicina ad O) al tempo t0 +l0/c. I due segnali
raggiungeranno contemporaneamente le due estremità dell’asta e queste
rifletteranno i due raggi verso O. Raggiungono
O al tempo tA e tB rispettivamente.
Le posizioni delle estremità
A e B dell’asta, utilizzando la 7) nel caso di allontanamento dell’asta
da O, saranno date da:
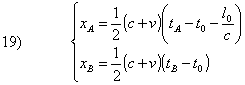
La lunghezza misurata l sarà data da:
(il termine 
è dovutoal fatto che
all’istante tB l’estremità B si è spostata ulteriormente rispetto alla sua
posizione nell’istante tA).
Sostituendo nella 20) le 19)
si ottiene l = l0 .
Dunque un solo osservatore
misurerà la stessa lunghezza per l’asta sia con metodo diretto che con metodo
indiretto, utilizzando i segnali luminosi. Solo se entra in scena un secondo
osservatore allora per accordarsi su i segnali da lanciare (simultaneità), per
confrontare le loro misure, si possono ottenere misure “relative”, “apparenti”
(contrazione, dilatazione, etc... e i loro paradossi22) dipendenti dalle convenzioni adottate.
APPENDICE
Introduzione dal preprint
della Comunicazione all’LXXXI Congresso Nazionale della S.I.F, data a Perugia
il 4ottobre 1995.
Critica delle usuali derivazioni delle
trasformazioni di lorentz.
P. Di Mauro, S. Notarrigo
G.N.S.F. — Sezione di
Catania
La stragrande maggioranza
dei fisici e dei filosofi della scienza è concorde nel ritenere che la
relatività ristretta di Einstein abbia introdotto profonde modifiche nelle
concezioni di spazio e tempo come definite nel contesto della fisica classica.
In particolare, secondo le
asserzioni della teoria einsteiniana, la lunghezza di un’asta e la durata di un
processo vengono a dipendere dallo stato di moto relativo, rettilineo e
uniforme, di due osservatori.
Molti si sono chiesti se tale importante
modifica sia solo “apparente” o “reale”.
Le risposte che vengono date a tale quesito
sono diverse in dipendenza del significato (mai esplicitamente definito) che
viene attribuito a tali aggettivi dai singoli ricercatori. Qualcuno banalizza
tale problema dicendo che tali aggettivi hanno a che fare con la filosofia e
non con la fisica. Ma altri fanno deduzioni a partire dal significato che
implicitamente danno ai detti termini.
Ma, come Peano notava, niente si può
“dedurre” se tutte le ipotesi del discorso non siano state esplicitamente
“asserite”.
Proveremo ad asserire alcune
ipotesi sul significato di tali termini in base all’uso di essi che se ne fa
comunemente in relazione a determinate situazioni osservative.
Gli astronomi misurano le
distanze tra gli astri a mezzo della parallasse. Naturalmente non si
sorprendono se, in base ad altri tipi di misurazioni indirette, trovano che il
rapporto tra due lunghezze il quale risulti minore di uno, quando misurato a mezzo
della parallasse, risulti maggiore di uno, quando calcolato a mezzo delle leggi
di forza; essi sanno che affinché la parallasse possa dare risultati coerenti
con quelle delle leggi di forza è necessario che le lunghezze da misurare
stiano alla stessa distanza dall’osservatore, per cui essi sono portati a dire
che le misure effettuate a mezzo della parallasse sono “apparenti” mentre le altre sono “reali”.
Da dove viene loro la convinzione
che le misure trovate a mezzo delle leggi di forza siano quantomeno più reali
di quelle effettuate a mezzo della parallasse? Si potrebbe pensare che ciò
dipenda dalla loro cieca credenza nelle leggi di Newton. Ma, ovviamente, non è
così. Infatti, nei casi in cui sia possibile misurare due lunghezze sia con la
parallasse che con il confronto diretto con l’unità di misura, scoprono che la
parallasse dipende sia dal la lunghezza effettiva dell’asta come misurata per
confronto diretto con l’unità di misura (e che quindi è una “proprietà”
dell’asta), sia dalla distanza dell’asta dal goniometro dell’osservatore
(distanza che si suppone misurata anch’essa per confronto diretto).
Quindi la parallasse non è
una proprietà dell’asta in quanto dipende anche da elementi estranei all’asta e
cioè dalla distanza dell’osservatore e dalle proprietà di propagazione della
luce, che si suppone propagarsi in modo rettilineo (naturalmente bisognerà
ammettere anche la validità della geometria euclidea).
Da quanto detto, possiamo
azzardare l’ipotesi che quando i fisici usano la contrapposizione “reale”, “apparente”, in relazione alle
grandezze fisiche, con il primo termine intendono il risultato di una misura
per confronto diretto, mentre l’altro lo usano quando la grandezza viene
misurata in modo indiretto e tale misura non coincide con la prima.
Marx nota, in un suo scritto23,come già Cicerone24 metteva in rilievo questo diverso uso dei due
termini in Democrito ed Epicuro: Democrito considera apparenza soggettiva la
realtà sensibile e attribuisce solo agli atomi e al vuoto lo statuto di realtà
oggettiva, capace di esistenza indipendente dal fatto che alcun essere possa
percepire il fenomeno da tale realtà sottostante causato ma, secondo Cicerone,
Epicuro rovescia tale criterio di realtà scrivendo che “i sensi sono tutti araldi del vero e che niente può confutare la
percezione sensibile”, per cui Cicerone conclude: “il sole sembra grande a Democrito, perché egli è uno scienziato ed ha
una compiuta conoscenza della geometria; della
grandezza di circa due piedi a Epicuro, perché egli pensa che esso è
grande tanto quanto appare”.
Ma vediamo come il criterio
di realtà che abbiamo sopra ipotizzato si confronta con le asserzioni della
relatività ristretta.
La relazione che lega tra
loro le lunghezze di un’asta rigida come effettuate da due osservatori, in moto
relativo rettilineo e uniforme tra loro, è data dalla relazione:
I) L’ = γ L
Generalmente non si
specifica se tale relazione si riferisca alle grandezze o ai numeri che le
misurano.
Infatti, dalla teoria delle
grandezze fisiche, sappiamo che non sono la stessa cosa.
Indichiamo con 
una “grandezza
fisica”, con 
un’altra “grandezza
fisica” che si assume come unità di misura, con l il “numero” che misura L in
rapporto ad 
.
La relazione tra grandezze e
numeri si suole esprimere con la formula:
Il) 
Se assumiamo che la I) si riferisca
alle grandezze, la relazione può essere scritta:
III) 
Poiché γ è una
grandezza adimensionata, noi siamo sempre liberi di includere25 il coefficiente γ o tra i valori (1’=
γ l con 
, questo è l’uso comune in fisica; con tale scelta si
realizza quello che si chiama un sistema di misurazione “coerente”, nel quale
le stesse formule si possono interpretare come valide sia per le grandezze che
per i numeri), o tra le unità di misura (1’=l con 
,un tale sistema di misurazione viene chiamato dai metrologi
“incoerente” e viene spesso usato dagli ingegneri perché nelle relazioni tra
numeri vengono a sparire tutti i coefficienti numerici) o, anche, possiamo
fare altre convenzioni più convenienti a seconda dei casi.
Con la prima scelta noi
siamo obbligati a misurare le due grandezze, riferentesi alla stessa asta, con
la “stessa” unità di misura. Non sapendo se effettivamente i regoli si
allunghino o si accorcino per effetto del movimento, se vogliamo essere sicuri
che l’unità di lunghezza sia la “stessa” dobbiamo effettuare le misure nello
stesso sistema di riferimento (dove abbiamo posto e fissato l’unità di misura)
e quindi con metodi diversi, l’una per confronto diretto, l’altra,
necessariamente, impiegando segnali luminosi. Non potremo mai decidere, in
questo caso, se il fatto che γ sia diverso da uno sia solo
apparenza, cioè dipendente dalla nostra convenzione sulle unità di misura, o
una modificazione effettiva delle lunghezze.
Con la seconda scelta, si
deve presupporre, fin dal principio, che l’allungamento dell’asta in moto sia
effettivo, essendo le unità di misura vere grandezze e non semplici numeri;
ma, in tal caso, i valori misurati dai due osservatori risulterebbero sempre
identici nei due sistemi e, quindi, entrambi gli osservatori sono legittimati
ad usare la meccanica classica e a non menzionare più il fatto che hanno
bisogno di segnali luminosi per comunicare, perché il fatto sarà irrilevante
per tutti i loro esperimenti che ognuno è obbligato a fare nel suo proprio
sistema, non potendone uscire fuori, in quanto misure per confronto diretto si
possono fare solo nello stesso sistema.
In questo caso L’ non
rappresenta la lunghezza dell’asta in moto come misurata dall’osservatore in
moto (concetto “a”) ma la lunghezza dell’asta in moto come misurata
dall’osservatore in quiete (concetto “b”).
Questa ambiguità tra i due concetti, “a” e “b”, si ritrova in tutti
quelli che scrivono sulla relatività a partire da Einstein, il quale cerca le
formule relative al concetto “a” ma ragiona come se si trattasse del concetto
“b”.
Potremmo ancora conven ire di porre:
o infinite altre convenzioni, senza che per questo
cambi il rapporto tra le lunghezze, cioè senza che cambi la fisica.
Lo stesso discorso vale per qualunque altra grandezza.
Esaminiamo formalmente le
implicazioni delle due ipotesi precedentemente considerate.
Poniamo dapprima:
,
i numeri sono sempre uguali nei due sistemi
ma le unità di misura non sono uguali nei due sistemi e se i due sistemi sono
in moto relativo fra di loro non è possibile un confronto diretto e dobbiamo
ricorrere a un modo indiretto per confrontare gli standard di lunghezza nei
due sistemi e in questo secondo caso non potremo più mantenere la (*).
Supponiamo di avere uno standard di velocità, p. es., un segnale di velocità data; supponiamo di avere due regoli filiformi tali che, quando confrontati per un tempo finito, necessario per il confronto diretto, siano relativamente in quiete; supponiamo di mettere in moto uno dei regoli, lungo l’asse, approssimativamente comune, dei due regoli; supponiamo, per definizione, che i due regoli abbiano la stessa lunghezza se a un dato istante gli estremi sinistro e destro dei due regoli coincidano perfettamente, il sinistro dell’uno con il sinistro dell’altro e il destro dell’uno con il destro dell’altro, allo stesso istante.
Per realizzare tale
confronto avremo bisogno di un sistema di coincidenza tra due segnali, p. es.
elettrici, luminosi, ecc., dovremmo essere in grado di posizionarci nel punto
di mezzo del nostro regolo e assicurarci che la differenza dei tempi tra le due
linee che portano i due segnali di coincidenza sia nulla.
E’ difficile fare un tale
esperimento quando uno dei due regoli sia in moto (se si vogliono realizzare
tutte queste condizioni) ma si può calcolare il risultato facendo l’ipotesi che
si abbiano segnali con velocità di propagazione costante.
Mediante il calcolo
scopriremo che i due regoli, che avevano lunghezza uguale quando confrontati in
quiete relativa tra loro (con entrambi i metodi di misura), non hanno la stessa
lunghezza quando confrontati con il sistema delle coincidenze tra i due segnali
di sovrapposizione degli estremi, e che la lunghezza varia con la velocità
relativa dei due regoli.
Una simile osservazione fu
il punto di partenza di Einstein.
Possiamo concludere intanto
che se vale la (*), qualunque sia γ
,anche dipendente dalla velocità relativa, non potremo mai sapere se ci sia
una reale modificazione delle lunghezze.
Il fatto che i numeri, in
questo caso, devono essere uguali, è dovuto al fatto banale, che se avessimo
graduato l’asta con un numero arbitrario, l,
di incisioni, tale numero di incisioni non può cambiare per il fatto che
ora l’asta (che per definizione è “rigida”, in quanto può essere assunta come
standard di lunghezza per entrambi i sistemi) è in moto rettilineo uniforme
con velocità arbitraria o anche di moto accelerato arbitrario, lo stesso vale
per l’unità di misura essendo una grandezza come le altre.
Questo comporta l’ipotesi
fisica che in entrambi i sistemi lo spazio è omogeneo e il tempo uniforme,
anche se separatamente. I due sistemi sono definiti solo dal diverso modo di
misurare tempi e lunghezze e questo esplicitamente assume Einstein nel famoso
lavoro del 1905.
Consideriamo ora il caso che
si abbia:
,
l’uguaglianza delle due grandezze, che rappresentano
le unità di misura nei due sistemi, dal momento che è impossibile un loro
confronto diretto, implica che l’unità di misura delle lunghezze è unica ed è
posta in uno dei due sistemi. Il fattore γ
posto tra i numeri è quello ottenuto per un confronto indiretto a mezzo di
segnali di velocità costante, come sopra chiarito e quindi è “apparente”,
secondo la nostra precedente definizione.
Infatti anche l’altro
osservatore compiendo le stesse operazioni trova la stessa cosa, ed è
impossibile credere che sia reale un effetto (allungamento dei regoli) che
appare identico per i due osservatori.
Qualcuno si avventura a
sostenere, in relazione al famoso paradosso dei gemelli, che l’effetto è reale
e avvertito “realmente” solo dal sistema che ha subito le accelerazioni26 (ci si chiede, rispetto a
quale sistema di riferimento viene misurata l’accelerazione, non si dice che
in relatività non esistono sistemi privilegiati?!).
Ma alcuni sostengono che
argomenti del tipo quelli avanzati dal Feynman non servono perché facendo
intervenire le accelerazioni si esce fuori dal quadro della relatività
ristretta. A nostro giudizio la ragione è più forte: anche introducendo campi
di forza reali o fittizi il problema del confronto tra le unità di misura viene
semplicemente spostato ma si ripresenta invariabilmente e immutato...
…Immaginiamo due sistemi di
riferimento in moto relativo, rettilineo, uniforme lungo un’arbitraria
direzione, con velocità 
.
Indichiamo con 
le coordinate di un evento che si produce in A come misurato da A, con 
le coordinate
dell’evento che si produce in A come
misurato da B e, analogamente, per un evento che si produce in B, indichiamo con 
e 
le coordinate misurate da A e B,
rispettivamente.
Se assumiamo che all’istante
si abbia 
, con le opportune
condizioni iniziali per la velocità, secondo la meccanica classica si hanno le
seguenti formule di trasformazione:
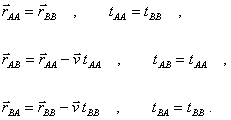
Le ultime due, a partire da
P. Franck, vengono delle “trasformazioni di Galileo”.
Se confondiamo le dette trasformazioni
tra loro arriviamo a degli insostenibili paradossi come analizzati dal Perucca27.
Consideriamo una sorgente in
A capace di sparare proiettili in
tutte le direzioni con velocità arbitraria, ma costante in modulo, diciamo c.
Consideriamo il fronte
d’onda della nuvola di proiettili sparati al tempo tAA = 0. Vista da A sarà una
superficie sferica di equazione:
vista da B
sarà una superficie ellittica di equazione:
Analogamente per una
sorgente posta in B.
In altre parole, se la
sorgente si trova nel sistema in cui le misure vengono effettuate appare
sferica, se si trova nell’altro sistema appare ellittica. E’ irrilevante quale
dei due sistemi si voglia ritenere in quiete (notiamo qui che lo spazio in
quiete assoluta non è di Newton ma è un’ invenzione di Eulero, la fisica di
Newton si può mettere in forma “assoluta”, cioè indipendente dal sistema di
coordinate e dalle unità di misura, cioè dalle misure relative, sensibili e
volgari di Newton, utilizzando il calcolo geometrico assoluto di Peano28).
Ma introducendo la
trasformazione di Voigt (illustre discepolo di Kirchhoff nel 1887 intraprese un
accurato e competente studio sulle implicazioni matematiche, e sulle relative
conseguenze fisiche, della equazione dell’onda in relazione all’effetto
Doppler, nel contesto della fisica classica come è ovvio, data l’epoca29) si può fare in modo che anche
A può scrivere l’equazione della
superficie sferica per una sorgente in B.
Naturalmente tale superficie
sferica non è quella che vedrebbe, effettuando le opportune misure; la
trasformazione è solo un artificio formale per cambiare la forma dell’equazione
e non la forma del fronte d’onda. Se i proiettili avessero una velocità diversa
da c il vantaggio formale verrebbe automaticamente perso, se si
volessero mantenere le trasformazioni ricavate con lo stesso valore della
precedente velocità.
In tutti gli scrittori di
relatività si riscontra l’ambiguità relativa a questa interpretazione delle
dette trasformazioni; in certi contesti sembra che si parli della quaterna di
numeri 
, in altri contesti
sembra che si parli dell’altra quaterna 
, come se la trasformazione non fosse più un semplice
artificio formale ma riguardasse le effettive misure che i due osservatori
compiono. E’ chiaro che finché nelle formule non intervengono le condizioni
iniziali non c’è differenza tra i vari casi; non è più così quando intervengano
le condizioni iniziali che sono diverse per i vari casi.
____________________________________
Qualche tempo dopo con Totò
Notarrigo tornammo sulla questione. Egli formalizzò le idee con queste altre
righe che qui trascrivo come furono lasciate.
Ipotesi e deduzioni
matematiche valide indipendentemente dal significato dei simboli.
Ipotesi:
a) S1 e S2 sono due sistemi lineari
unidimensionali, S1 ¹ S2
b) O1 e O2 sono due campi commutativi che rappresentano
i campi degli operatori di S1 e S2 rispettivamente.
c) Esiste
una corrispondenza lineare tra gli individui di S1 e S2 .
Deduzioni:
Per a), b):
(1) 
,
(2) 
,
per c):
(3) 
,
(4) 
.
Per(1), (2) e (3):
(5) 
,
da (4) e (5):
(6) 
,
ovvero:
(7) l2
= l1 .
Queste ipotesi corrispondono
all’ipotesi originale di Einstein per cui un regolo di lunghezza unitaria 
messo in moto “appare” di lunghezza 
.
Bisogna dire “appare” perché
ognuno dei due osservatori vede il regolo accorciarsi e, dal momento che il
regolo è lo stesso, non può essere più corto per entrambi gli osservatori in
moto relativo tra loro, quindi si deve concludere che la relazione si riferisce
alle grandezze e non ai numeri, allora γ è un numero che
rappresenta il rapporto tra le due lunghezze misurate con metodi diversi.
Supponiamo ora di aggiungere
l’ipotesi:
d) Esiste una corrispondenza
lineare tra gli individui di O1
e O2 ma esiste uno
standard di lunghezza che resta invariato per effetto del movimento, ciò
equivale a porre 
.
Ciò implica:
(8) 
,
quindi:
(9) 
.
Questo significa che,
rispetto allo standard, le varie aste si allungano effettivamente quando sono
in moto.
Ma, nella teoria della relatività,
l’ipotesi dello standard indipendente dal movimento non è prevista.
Ancora una volta dobbiamo
concludere che in detta teoria si vogliono confrontare diversi metodi di
misura e non un effettivo allungamento dei regoli.
L’idea di confrontare due
regoli per mezzo delle coincidenze, “contemporanee”, fra gli estremi di due
regoli equivale a una misura col metodo indiretto. I due osservatori in moto
relativo misureranno, per lo stesso regolo, numeri diversi, perché se i due
eventi sono contemporanei per l’uno non saranno contemporanei per l’altro,
esattamente come nel primo dei due casi che abbiamo sopra esaminato. Ciò,
naturalmente, se i due osservatori usano lo stesso metodo. Così resta
arbitraria la definizione di uno standard unico e possiamo assumere,
convenzionalmente, che la lunghezza “reale” dello standard è quella del
riferimento in cui la misura diretta coincide con quella indiretta. Ma ora
abbiamo creato un osservatore privilegiato che è unico, e tutti gli altri
osservatori, che si muovono rispetto ad esso di moto traslatorio uniforme con
velocità non nulla, osserveranno solo misure apparenti, in quanto per essi i
due metodi daranno sempre risultati diversi.
Tutto questo resta vero con
le sole ipotesi di Einstein, anche per le trasformazioni più generali di
quelle di Lorentz, che con tali ipotesi si possono ricavare.
Si conclude che l’ipotesi,
sottintesa da Einstein, che la coincidenza dei risultati per i due metodi di
misura possa essere sempre valida per tutti gli osservatori, non può essere
mantenuta e il principio di relatività vale solo per le misure eseguite con lo
stesso metodo, che può solo essere quello delle misure indirette, con risultati
“apparenti” e non “reali”.
NOTE
1 cfr “L’anno memorabile di Einstein”, a cura di J. Stachel, Ed. Dedalo,
2001, pp. 138— 140. TORNA
2 G. Galilei: “Discorsi intorno a due nuove scienze — Giornata terza — Del moto locale” (1638), UTET, p. 722. TORNA
3 G. Galilei: “Dialogo sui massimi sistemi — Giornata prima’’ (1632), UTET, p. 41. TORNA
4 G. Galilei: “Discorsi intorno a due nuove scienze — Giornata terza — Del moto locale” (1638), UTET, p. 726. TORNA
5 P.W. Bridgman: “La logica della fisica moderna”, Boringhieri
(TO), 1977, p.110. TORNA
6 cfr. G. Boscarino, S.
Notarrigo, A. Pagano: “Geometria e
fisica” in Mondotre/Quaderni, Anno IV— Numero 8— Novembre 1992, Ed.
Cooperativa Laboratorio (SR), pp. 88—89. TORNA
7 G. Peano: “Opere scelte”, VoIII, “Sui
fondamenti della geometria”, Ed. Cremonese(1959), pp.141—142. TORNA
8 cfr G. Peano, op. cit., p. 436. TORNA
9 cfr. nota l, pp.
140—141. TORNA
10 A. Einstein. ‘‘Come io vedo il mondo’’, Tascabili Newton (1988), p.
79. TORNA
11 cfr. nota l, p. 140. TORNA
12 cfr. P. Di Mauro,
Mondotre/La Scuola Italica—AnnoI — Numero 1—Dicembre1999, p. 15 e relativa
bibliografia; S. Marinov, Found. of Phys., 9,445 (1979); C. Giannoni, Found. of
Phys., 9,427 (1972), A. R. Lee, T. M. Kalatos, Am. J. Phys. 9, 870(1977). TORNA
13 P. Di Mauro, S.
Notarrigo: “Sull’invarianza delle
equazioni di Maxwell”, Atti del XVI Congresso Nazionale di Storia
della Fisica e dell’Astronomia, Como 1996 (a cura di P. Tucci), Gruppo di
lavoro per le Celebrazioni Voltiane, CNR, maggio 1997,(MI),p.335; anche sul
sito internet: http:// albinoni.brera.unimi.it/Atti-Como-1996. TORNA
14
Per le questioni relative alle unità di misura e agli
effetti “reali” o “apparenti” si rimanda all’Appendice a questo scritto. TORNA
15 cfr. W.G.V. Rosser, “Relativity”,
Butterworths, London
(1967), App. 6: “Radar Methods and the
k-calculus”, p.319. TORNA
16 C. Giannoni, op. cit.
nota 12; E. Feenberg, Found. of Phys., 9, 329(1979). TORNA
17 H. Bondi: “Miti e ipotesi della teoria fisica”- Zanichelli,
1971, p.52 TORNA
18 cfr. Appendice a questo
scritto; P. Di Mauro, op. cit. nota 12; A. Pagano, Mondotre/ La scuola
Italica—Anno II, numero 2— Dicembre 2000- Nuova serie; H. Dingle, Nature,
195(1962), p. 985; M. Born, Nature, 197(1963) p. 1287; H. Dingle, Nature,
197(1963), p. 1248, p. 1287. TORNA
19 cfr. Appendice a questo
scritto. TORNA
20 cfr. op. cit. nota 16. TORNA
21 cfr.op. cit. nota l.
pp. 141-143. TORNA
22
cfr.Appendice a questo scritto; op. cit. nota 18; W.
Rindler; Am. J. Phys.,29,365 (196l) e 38.1111 (1970); Ya. A. Smodinskii, V. A.
Ugarov, Soviet Physics Uspekhi, 15,340(1972); i. A. Zinnie, Am. J. Phys., 40,
1091 (1972). TORNA
23 K. Marx, “Democrito e Epicuro”, dissertazione dottorale in appendice al libro di
A. Sabetti, ‘‘Sulla fondazione del
materialismo storico’’, La Nuova Italia, Firenze, 1962. TORNA
24 Cicerone, “De Fin.” 1, 6, 20. TORNA
25 cfr. E. Perucca, “Fisica Generale e Sperimentale”, UTET;
cfr. anche G. Peano, “Operazioni sulle grandezze”, in “Opere scelte di G. Peano”, a cura di U. Cassina, vol. III, p. 435
e segg. TORNA
26 R. P. Feynman, “The Feynman
Lectures on Physics”, Addison Wesley, 1966, I, 1, 16- 3. TORNA
27 cfr. E. Perucca, op.
cit. nota 25, p. 261. TORNA
28 cfr. S. Notarrigo, “A ppunti di Fisica Superiore”, non
pubblicati. TORNA
29 W. Voigt, “Uber das Doppler’sche Princip”, Nachrichten
der Konigliche Gesellschaft der Wissenschaften zu Gottingen, 10 Marz 1887. TORNA