CONSIDERAZIONI
INTORNO ALLA
CATENA LINEARE VIBRANTE
Giuseppe Garozzo
1-Introduzione
Date le difficoltà
matematiche in cui ci si imbatte quando si tenta di risolvere un problema dinamico
in presenza di più di due corpi, si è soliti formulare modelli di sistemi ad N
particelle con delle peculiarità tali da rendere fattibile la loro risoluzione
analitica. Uno di questi modelli è fornito dalla catena lineare tridimensionale
costituita da N punti ed N+1 molle. In questo lavoro noi
ripercorreremo le tappe della già nota risoluzione analitica in termini di
equazioni di Newton e faremo delle osservazioni originali che ci condurranno
sia nella meccanica quantistica che nella relatività. Ma si badi bene che tali
“intromissioni” saranno eseguite senza uscire dall’ambito della meccanica
classica pertanto speriamo che siano utili per comprendere meglio il legame
fra tutte queste tre teorie.
2 - Il modello
Considetiamo N
particelle il cui raggio vettore lo indichiamo con ![]() (i=1,2,...,N) di
massa m. Secondo la meccanica classica la lagrangiana del sistema è data dalla
seguente espressione:
(i=1,2,...,N) di
massa m. Secondo la meccanica classica la lagrangiana del sistema è data dalla
seguente espressione:
![]()
A questo punto
introduciamo le seguenti ipotesi:
1. l’interazione
è presente solo fra due particelle contigue;
2. esiste
una configurazione di equilibrio;
3. la
prima e l’ultima particella sono vincolate e sono poste ad una distanza l.
Per l’ipotesi 1 e 2,
il modello si riduce a quello di una catena lineare tridimensionale di N+ 1
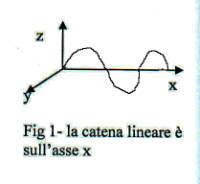
molle ed N particelle. Supporremo di utilizzare le coordinate esposte in figura
1 e pertanto supporremo che la prima e l’ultima particella siano vincolate
sull’asse x.
La lagrangiana
pertanto si può scrivere in questo modo:
![]()
dove ( xn , yn , zn )
è la
coordinata della n-esima particella e k è
la derivata seconda dell’energia potenziale calcolata nella configurazione
d’equilibrio.
Le equazioni del
moto sono pertanto [1]:

Come si può evincere dalla referenza
[1], un tale sistema ammette per la
variabile y e z la configurazione d’equilibro (0,0,.., 0), mentre per la variabile x la configurazione (a,2a,...,Na), dove a=l/(N+1).
Se ora introduciamo i seguenti scostamenti:

Le equazioni del moto assumono la seguente
forma.
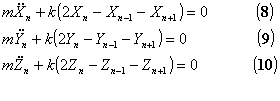
Osserviamo che tutte queste espressioni sono invarianti per trasformazioni di Galileo; quest’ultime per le equazioni 2,3 e 4 si possono scrivere in questa forma:
![]()
dove ovviamente v è la velocità del riferimento ‘apicato’
che si muove rispetto al primo con una velocità uniforme lungo l’asse x. Il
fatto che esse risultino invarianti per trasformazioni di Galileo è una cosa
banale dal momento che esse non sono altro che le equazioni di Newton. Vorrei
inoltre osservare che in questo caso concernente un sistema di N particelle,
le equazioni che esprimono le trasformazioni di Galileo sono 3N. Per quanto
concerne le equazioni 8,9 e 10 dato che le variabili che vi compaiono sono
degli scostamenti, le corrispondenti trasformazioni di Galileo sono:
![]()
3 - Il
passaggio al continuo
Se ora supponiamo
che N sia molto grande rispetto a l e che quindi a sia trattabile
come una quantità infinitesima, possiamo eseguire il passaggio al limite nelle
equazioni 8, 9 e 10. Per semplicità di trattazione limitiamo per ora il
passaggio al continuo solo per le oscillazioni nell’asse x (per l’estensione al
caso tridimensionale basta ripetere le stesse considerazioni fatte per la
componete sull’asse x); in tal caso bisogna introdurre una funzione ψ =
ψ (x) che dà gli scostamenti della corda lungo l’asse x in funzione
appunto della posizione sull’asse x. In tal caso è facile mostrare che la 10 diventa [2]:
![]()
Come poi sappiamo essa rappresenta
l’equazione d’onda che descrive onde propagantesi con velocità c data dalla:
![]()
Si è soliti dire che la (11) non è invariate
per trasfonnazioni di Galileo, ma in che senso? La (11) proviene dalla (10)
quando si effettua il passaggio dal discreto al continuo, ma in questo
passaggio come si devono riscrivere le trasfonnazioni di Galileo, cioé le (11)?
Storicamente si è detto [3] che la (11) non è
invariante per la seguente trasformazione di Galileo:
![]()
Il che è vero, ma
la (12) è la corretta trasformazione di Galileo?
Ovviamente la (11)
è la corretta trasformazione di Galileo applicata ad una particella; qui
abbiamo N particelle che, peraltro, sono, in questa approssimazione,
distribuite con continuità. A questo punto possiamo rovesciare il problema,
ponendoci il problema matematico di trovare una relazione fra x’, x e t in modo che l’equazione delle onde
abbia la stessa forma anche in un altro riferimento. In questo caso la
trasformazione cercata è quella di Voigt-Lorentz:
![]()
dove

Osserviamo come per
c molto maggiore di v le (14) si riducono alle (13) (ovviamente nel caso in cui
x non tenda ad infmito!).
Da un punto di
vista formale il passaggio al limite fra il discreto ed il continuo implica il
passaggio da una equazione del moto in forma differenziale ad una equazione
alle derivate parziali. Questa osservazione è in accordo col fatto che per c molto grande la derivata parziale
rispetto alla t può essere trascurata e l’equazione 11 può essere interpretata
come una equazione differenziale.
4—Primi commenti
Soffermiamoci
brevemente sulla 12. Dato che ka2 è l’energia di legame nella
configurazione d’equilibrio per la generica particella, possiamo scrivere la
seguente equazione:
E=mc2 (15)
che ci fornisce
l’energia di legame in funzione della velocità di fase dell’oscillazione. La
(15) è la ben nota equazione relativistica di equivalenza fra massa ed energia.
In questo caso è stata ricavata da un modello classico senza grossi sforzi.
Per quanto concerne
poi la soluzione della 11 essa è data da una combinazione lineare di funzioni
del tipo:
exp i(k x - ωt) e exp
i(k x + ωt)
esse descrivono
rispettivamente perturbazioni che si propagano sull’asse x da sinistra a destra
e viceversa. La quantità k è l’inverso della lunghezza d’onda moltiplicata per 2π mentre ω è la frequenza sempre moltiplicata per 2 π.
Sostituendole
nell’equazione delle onde si ricava: ω
2=(kc)2 ovvero ω =± k c
dove c rappresenta la velocità di
propagazione della perturbazione.
Adesso vorrei
sintetizzare i punti per me più salienti fin qui ottenuti. Ebbene, una volta
effettuato il passaggio dal discreto al continuo abbiamo dimostrato che:
- non siamo più interessati alla dinamica dei singoli costituenti della catena, bensì alla propagazione della perturbazione che nel nostro caso si manifesta come una cresta sull’asse z e che si propaga sull’asse x;
- questa
perturbazionè è descritta da tre parametri: la velocità
di fase c (che in questo caso ci
fornisce la velocità di propagazione dell’onda), il vettore d’onda k (che in pratica descrive la lunghezza
d’onda» e la pulsazione ω (in pratica la frequenza);
- l’equazione
d’onda stabilisce che ci sono due onde una propagantesi con velocità c
e l’altra con velocità -c;
- la
relazione fra questi tre parametri è: ω 2 -
(kc)2 = 0;
- la
velocità di propagazione c è
legata all’energia di legame nella posizione di
equilibrio
di una arbitraria particella di massa m dalla:
E = mc2 .
Il fatto che ci
sono due tipi di onde, una che si muove nel verso positivo, l’altra nel verso
negativo è in relazione con un problema più ampio noto come problema del
potenziale anticipato e ritardato. In questa sede mi limiterò solo ad
osservare quanto questo problema sia legato al carattere prettamente ncwtoniano
della forza. Infatti in meccanica classica l’interazione fra due o più
particelle dipende solo dalla distanza e pertanto essa prende luogo
istantaneamente; invece la perturbazione dovuta a un cambio di posizione di una
particella può in generale avere una velocità finita Mi spiego meglio. In
questo modello se io ad esempio perturbo la prima particella della catena
genero due onde. Una si propaga verso gli altri elementi della catena, l’altra
invece parte dall’estremo della catena e si propaga verso la particella
perturbata. Quest’ultima di solito si dice che non ha significato fisico;
invece rappresenta la perturbazione dovuta al contorno della catena in accordo
col principio di azione e reazione. Non voglio dilungarmi più su questo punto
assai interessante, ma mi limito solo ad osservare che quando si ha a che fare
con una equazione d’onda le soluzioni sono sempre di due tipi: un’onda
propagantesi in avanti ed una propagantesi all’indietro.
5—Catena lineare soggetta a
perturbazioni adiabatiche
Ritorniamo adesso
alla catena nel caso discreto e supponiamo adesso che la nostra catena sia
soggetta ad un potenziale perturbativo variabile nel tempo la cui intensità sia
molto debole e la cui variazione avviene in tempi lunghissimi se paragonati con
le frequenza della catena (perturbazione adiabatica).
Come si può
dimostrare in questo caso la catena di oscillatori accoppiati è equivalente ad
un sistema di oscillatori non accoppiati di massa unitaria e con una data
pulsazione ùi. Si osservi come nel caso discreto si hanno solo N frequenze mentre nel caso continuo esse sono infinite.
Quindi
-nel passaggio dal
discreto al continuo si perde la discretizzazione delle frequenze.
Se adesso ci
chiediamo non quale sia l’energia meccanica del singolo oscillatore della
catena, ma l’energia che esso è capace di cedere all’ambiente esterno per via
di un potenziale perturbativo adiabatico, allora la risposta, grazie alla
teoria degli invarianti adiabatici [3], è
E=hù (16)
dove h
è una costante di proporzionalità avente dimensioni opportune.
Cioè:
- l’energia
che la catena può cedere all’ambiente esterno è sempre proporzionale alla
frequenza di un suo modo di vibrazione.
Gli sconfinamenti nella meccanica quantistica non sono terminati. Infatti in questo modello possiamo sempre associare una quantità di moto p ad una particella arbitraria della catena quando essa viene posta in movimento dall’onda.
Infatti possiamo
porre:
p=mc
Se adesso
identifichiamo le energie date dalla 14 e
dalla 16 abbiamo
p
= E/c
quindi
p =
hù/c
ed in defmitiva si
perviene alla relazione di De Broglie
p =
hk
dove k ricordiamo è il vettore d’onda. Vorrei
infine sottolineare come l’espressione E=mc2
può essere intesa non solo come energia di legame. Infatti visto che
possiamo associare un’onda ai punti materiali della catena, possiamo sempre
dire che ad ogni istante esisterà un punto materiale che si muove con velocità
c. E dato che per un potenziale armonico l’energia cinetica media è
eguale all’energia potenziale media, a questo elemento possiamo sempre
associare un’energia pari a due volte quella cinetica, ovvero mc2.
6— Discussioni
Quanto sin qui
esposto dimostra come sia possibile costruire un modello “meccanico” per mezzo
del quale possiamo disanimare alcuni risultati della fisica moderna. Ma l’uso
di un modello così semplice ci permette di chiarire alcuni punti che
attualmente sono assai oscuri, quale ad esempio il problema dell’invarianza
delle equazioni del moto. Da un punto di vista fondamentale, la presunta
discrasia esistente fra le leggi della dinamica (equazione di Newton) e le
leggi dell’elettromagnetismo (equazione alla derivate parziali di Maxwell) è
stata foriera di tutta una serie di innovazioni quali ad esempio l’av-vento
della teoria della Relatività. Tuttavia visto il naufragio della fisica moderna
(mi riferisco alla teoria delle particelle) secondo me è necessario rivedere
quelle che vengono ritenute conquiste solide soprattutto mettendole alla prova
nell’interpretare modelli semplici come quello di una catena lineare. Infatti
in questa maniera si scopre come il problema dell’invarianza non sia così
scontato come forse si potrebbe credere a prima vista. Si scopre come la natura
ondulatoria della materia non necessariamente ci deve indurre a porci domande
assurde sulla dualità della materia. In sintesi forse scopriamo che le
soluzioni che in questo secolo la fisica teorica ha portato per superare delle
difficoltà, forse, non hanno fatto altro che mascherare queste difficoltà
introducendo tutta una serie di elementi metafisici privi di riscontro diretto
come ad esempio la contrazione della lunghezza e la dilatazione del tempo.
Ovviamente ogni teoria ha bisogno di elementi metafisici da cui partire,
l’importante è che questi siano controllabili mediante
l’uso di modelli elementari. Soluzioni che sembrano momentaneamente risolvere
qualche problema ma che rendono oscure le idee, alla fine non faranno altro che
generare confusione. Ebbene in questo clima di confusione è necessario rivedere
le nostre conoscenze partendo da cose semplici e, soprattutto, riaprendo
problemi che sono stati ritenuti ormai risolti.
Bibliografia
[1] Problemi di Meccanica Razionale, Bampi-Benati-Morro,
Ed. ECIG
[2] Meccanica Razionale, B.Finzi, Ed. Zanicheli
[3] Meccanica, Landau-Lifsits, Ed. Editori Riuniti