Comunicazione al LXXXI CONGRESSO NAZIONALE SIF, 4 Ottobre 1995, Perugia

Critica delle usuali derivazioni delle trasformazioni di Lorentz

P. Di Mauro, S. Notarrigo

G. N. S. F., Sezione di Catania

La stragrande maggioranza dei fisici e dei filosofi della scienza è concorde nel ritenere che la relatività ristretta di Einstein abbia introdotto profonde modifiche nelle concezioni di spazio e tempo come definite nel contesto della fisica classica.

In particolare, secondo le asserzioni della teoria einsteiniana, la lunghezza di un’asta e la durata di un processo vengono a dipendere dallo stato di moto relativo, rettilineo e uniforme, di due osservatori.

Molti si sono chiesti se tale importante modifica sia solo “apparente” o “reale”.

Le risposte che vengono date a tale quesito sono diverse in dipendenza del significato (mai esplicitamente definito) che viene attribuito a tali aggettivi dai singoli ricercatori. Qualcuno banalizza tale problema dicendo che tali aggettivi hanno a che fare con la filosofia e non con la fisica. Ma altri fanno deduzioni a partire dal significato che implicitamente danno ai detti termini.

Ma, come Peano notava, niente si può “dedurre” se tutte le ipotesi del discorso non siano state esplicitamente “asserite”.

Proveremo ad asserire alcune ipotesi sul significato di tali termini in base all’uso di essi che se ne fa comunemente in relazione a determinate situazioni osservative.

Gli astronomi misurano le distanze tra gli astri a mezzo della parallasse.

Naturalmente non si sorprendono se, in base ad altri tipi di misurazioni indirette, trovano che il rapporto tra due lunghezze che risulti minore di uno, quando misurato a mezzo della parallasse, risulti maggiore di uno, quando calcolato a mezzo delle leggi di forza; essi sanno che affinché la parallasse possa dare risultati coerenti con quelle delle leggi di forza è necessario che le lunghezze da misurare stiano alla stessa distanza dall’osservatore, per cui essi sono portati a dire che le misure effettuate a mezzo della parallasse sono “apparenti” mentre le altre sono “reali”.

Da dove viene loro la convinzione che le misure trovate a mezzo delle leggi di forza siano quantomeno più reali di quelle effettuate a mezzo della parallasse? Si potrebbe pensare che ciò dipenda dalla loro cieca credenza nelle leggi di Newton. Ma, ovviamente, non è così. Infatti, nei casi in cui sia possibile misurare due lunghezze sia con la parallasse che con il confronto diretto con l’unità di misura, scoprono che la parallasse dipende sia dalla lunghezza effettiva dell’asta come misurata per confronto diretto con l’unità di misura (e che quindi è una “proprietà” dell’asta), sia dalla distanza dell’asta dal goniometro dell’osservatore (distanza che si suppone misurata anch’essa per confronto diretto).

Quindi la parallasse non è una proprietà dell’asta in quanto dipende anche da elementi estranei all’asta e cioè dalla distanza dell’osservatore e dalle proprietà di propagazione della luce, che si suppone propagarsi rettilineamente (naturalmente bisognerà ammettere anche la validità della geometria eucidea).

Da quanto detto, possiamo azzardare l’ipotesi che quando i fisici usano la contrapposizione “reale”, “apparente”, in relazione alle grandezze fisiche, con il primo termine intendono il risultato di una misura per confronto diretto, mentre l’altro lo usano quando la grandezza viene misurata in modo indiretto e tale misura non coincida con la prima.

Marx nota, in un suo scritto,¹ come già Cicerone² metteva in rilievo questo diverso uso dei due termini in Democrito ed Epicuro: Democrito considera apparenza soggettiva la realtà sensibile e attribuisce solo agli atomi e al vuoto lo statuto di realtà oggettiva, capace di esistenza indipendentemente dal fatto che alcun essere possa percepire il fenomeno da tale realtà sottostante causato ma, secondo Cicerone, Epicuro rovescia tale criterio di realtà scrivendo che “i sensi sono tutti araldi del vero e che niente può confutare la percezione sensibile”, per cui Cicerone conclude: “il sole sembra grande a Democrito, perché egli è uno scienziato ed ha una compiuta conoscenza della geometria; della grandezza di circa due piedi a Epicuro, perché egli pensa che esso è grande tanto quanto appare”.

Ma vediamo come il criterio di realtà che abbiamo sopra ipotizzato si confronta con le asserzioni della relatività ristretta.

La relazione che lega tra loro le lunghezze di un’asta rigida come effettuate da due osservatori, in moto relativo rettilineo e uniforme tra loro, è data dalla relazione

(1) L’ = γ L

Generalmente non si specifica se tale relazione si riferisce alle grandezze o ai numeri che li misurano.

Infatti, dalla teoria delle grandezze fisiche, sappiamo che non sono la stessa cosa.

Indichiamo con L una “grandezza fisica”, con un’altra “grandezza fisica” che si assume come unità di misura, con l il “numero” che misura L in rapporto ad .

La relazione tra grandezze e numeri si suole esprimere con la formula:

(2)

Se assumiamo che la (1) si riferisca alle grandezze, la relazione può essere scritta

(3) .

Poiché γ è una grandezza adimensionata, noi siamo sempre liberi di includere³ il coefficiente γ o tra i valori ( l’= γ l con ) (questo è l’uso comune in fisica, con tale scelta si realizza quello che si chiama un sistema di misurazione “coerente”, nel quale le stesse formule si possono interpretare come valide sia per le grandezze che per i numeri), o tra le unità di misura (l’=l con ,) (un tale sistema di misurazione viene chiamato dai metrologi “incoerente” e viene spesso usato dagli ingegneri perché nelle relazioni tra numeri vengono a sparire tutti i coefficienti numerici) o, anche, possiamo fare altre convenzioni più convenienti a seconda dei casi.

Con la prima scelta noi siamo obbligati a misurare le due grandezze, riferentesi alla stessa asta, con la “stessa” unità di misura. Non sapendo se effettivamente i regoli si allunghino o si accorcino per effetto del movimento, se vogliamo essere sicuri che l’unità di lunghezza sia la “stessa” dobbiamo effettuare le misure nello stesso riferimento (dove abbiamo posto e fissato l’unità di misura) e quindi con metodi diversi, l’una per confronto diretto, l’altra, necessariamente, impiegando segnali luminosi. Non potremo mai decidere, in questo caso, se il fatto che γ sia diverso da uno sia solo apparenza, cioè dipendente dalla nostra convenzione sulle unità di misura, o una modificazione effettiva delle lunghezze.

Con la seconda scelta, si deve presupporre, fin dal principio, che l’allungamento dell’asta in movimento sia effettivo, essendo le unità di misura vere grandezze e non semplici numeri; ma, in tal caso, i valori misurati dai due osservatori risulterebbero sempre identici nei due sistemi e, quindi, entrambi gli osservatori sono legittimati ad usare la meccanica classica e a non menzionare più il fatto che hanno bisogno di segnali luminosi per comunicare, perchè il fatto sarà irrilevante per tutti i loro esperimenti che ognuno è obbligato a fare nel suo proprio sistema, non potendone uscire fuori, in quanto misure per confronto diretto si possono fare solo nello stesso sistema.

In questo caso L’ non rappresenta la lunghezza dell’asta in moto come misurata dall’osservatore in moto (concetto ‘a’) ma la lunghezza dell’asta in moto come misurata dall’osservatore in quiete (concetto ‘b’).

Questa ambiguità tra i due concetti, ‘a’ e ‘b’, si ritrova in tutti quelli che scrivono sulla relatività a partire da Einstein, il quale cerca le formule relative al concetto ‘a’ ma ragiona come se si trattasse del concetto ‘b’.

Potremmo ancora convenire di porre:

o infinite altre convenzioni, senza che per questo cambi il rapporto tra le lunghezze, cioè senza che cambi la fisica.

Lo stesso discorso vale per qualunque altra grandezza.

Esaminiamo formalmente le implicazioni delle due ipotesi precedentemente considerate.

Poniamo dapprima:

(*) ,

i numeri sono sempre uguali nei due sistemi ma le unità di misura non sono uguali nei due sistemi e se i due sistemi sono in moto relativo fra di loro non è possibile un confronto diretto e dobbiamo ricorrere a un modo indiretto per confrontare gli standard di lunghezza nei due sistemi e in questo secondo caso non potremo più mantenere la (*).

Supponiamo di avere uno standard di velocità, p. es., un segnale di velocità data; supponiamo di avere due regoli filiformi tali che, quando confrontati per un tempo finito, necessario per il confronto diretto, siano relativamente in quiete; supponiamo di mettere in moto uno dei regoli, lungo l’asse, approssimativamente comune, dei due regoli; supponiamo, per definizione, che i due regoli abbiano la stessa lunghezza se a un dato istante gli estremi sinistro e destro dei due regoli coincidono perfettamente, il sinistro dell’uno con il sinistro dell’altro e il destro dell’uno con il destro dell’altro, allo stesso istante.

Per realizzare tale confronto avremo bisogno di un sistema di coincidenza tra due segnali, p. es. elettrici, luminosi, ecc., dovremmo essere in grado di posizionarci nel punto di mezzo del nostro regolo e assicurarci che la differenza dei tempi tra le due linee che portano i due segnali di coincidenza sia nulla.

È difficile fare un tale esperimento quando uno dei due regoli sia in moto (se si vogliono realizzare tutte queste condizioni) ma si può calcolare il risultato facendo l’ipotesi che si abbiano segnali con velocità di propagazione costante.

Mediante il calcolo, scopriremo che i due regoli, che avevano lunghezza uguale quando confrontati in quiete relativa tra loro (con entrambi i metodi di misura), non hanno la stessa lunghezza quando confrontati con il sistema delle coincidenze tra i due segnali di sovrapposizione degli estremi, e che la lunghezza varia con la velocità relativa dei due regoli.

Una simile osservazione fu il punto di partenza di Einstein.

Possiamo concludere intanto che se vale la (*), qualunque sia γ, anche dipendente dalla velocità relativa, non potremo mai sapere se ci sia una reale modificazione delle lunghezze.

Il fatto che i numeri, in queso caso, devono essere uguali, è dovuto al fatto banale, che se avessimo graduato l’asta con un numero arbitrario, l, di incisioni, tale numero di incisioni non può cambiare per il fatto che ora l’asta (che per definizione è “rigida”, in quanto può essere assunta come stardard di lunghezza per entrambi i sistemi) è in moto rettilineo uniforme con velocità arbitraria o anche di moto accelerato arbitrario, lo stesso vale per l’unità di misura essendo una grandezza come le altre.

Questo comporta l’ipotesi fisica che in entrambi i sistemi lo spazio è omogeneo e il tempo uniforme, anche se separatamente. I due sistemi sono definiti solo dal diverso modo di misurare tempi e lunghezze e questo esplicitamente assume Einstein nel famoso lavoro del 1905.

Consideriamo ora il caso che si abbia

(**)

l’uguaglianza delle due grandezze, che rappresentano le unità di misura nei due sistemi, dal momento che è impossibile un loro confronto diretto, implica che l’unità di misura delle due lunghezze è unica ed è posta in uno dei due sistemi. Il fattore γ posto tra i numeri è quello ottenuto per un confronto indiretto a mezzo di segnali di velocità costante, come sopra chiarito e quindi è “apparente”, secondo la nostra precedente definizione.

Infatti anche l’altro osservatore compiendo le stesse operazioni trova la stessa cosa, ed è impossibile credere che sia reale un effetto (l’allungamento dei regoli) che appare identico per i due osservatori.

Qualcuno si avventura a sostenere, in relazione al famoso paradosso dei gemelli, che l’effetto è reale e avvertito “realmente” solo dal sistema che ha subito le accelerazioni⁴ (ci si chiede, rispetto a quale sistema di riferimento viene misurata l’accelerazione, non si dice che in relatività non esistono sistemi privilegiati?!).

Ma alcuni sostengono che argomenti del tipo di quelli avanzati dal Feynman non servono perchè facendo intervenire le accelerazioni si esce fuori dal quadro della relatività ristretta. A nostro giudizio la ragione è più forte: anche introducendo campi di forza reali o fittizi il problema del confronto tra le unità di misura viene semplicemente spostato ma si ripresenta invariabilmente e immutato.

Quindi ci è sembrato opportuno riprendere le varie ipotesi (implicite od esplicite) che si fanno per arrivare alle trasformazioni di Lorentz a partire da quella originale di Einstein.

Ma prima è utile e interessante esaminare l’origine storica di dette trasformazioni, oggi dette “di Lorentz”.

Nel 1887 un illustre discepolo di Kirchhoff, W. Voigt, intraprese un accurato e competente studio sulle implicazioni matematiche, e sulle relative conseguenze fisiche, della equazione dell’onda, in relazione all’effetto Doppler, nel contesto della fisica classica come è ovvio, data l’epoca.⁵

La questione fu ripresa, in seguito, da Lorentz⁶ e successivamente considerata in connessione con i problemi sollevati dagli aspetti interpretativi della teoria della relatività ristretta.⁷

Ne daremo un cenno seguendo il riassunto che ne danno Burali - Forti e Boggio.⁸

Voigt si pone il problema seguente: si considerino due “mezzi” nei quali si propaghino delle onde provenienti da certe sorgenti, fisse nell’uno ma animate invece di un moto uniforme nell’altro, la perturbazione che a un istante t avviene in un punto P del primo mezzo, si riproduce, a un certo istante t’, in un certo punto P’ del secondo. Ciò significa che deve esistere una corrispondenza fra i punti e gli istanti di tempo del primo mezzo e quelli del secondo mezzo, determinata dalle condizioni che si vorranno imporre tra le corrispondenti perturbazioni.

D’Alembert aveva già trovato la soluzione dell’equazione dell’onda.

Nel caso tridimensionale, l’equazione dell’onda e:

(4)

e la soluzione generale è:

(5) .

Un integrale particolare è:

(6) ,

che rappresenta un’onda sferica propagantesi in un mezzo, a partire da una sorgente posta nel punto O, origine degli assi coordinati di riferimento.

Siano x, y, z, t le coordinate spazio-temporali di un punto P e operiamo la trasformazione:

.

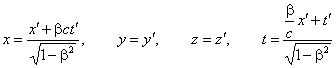La (6) ci darà un altro integrale della trasformata della (4), (che, tuttavia, resta invariata in forma) e rappresenta, ancora, un’altra onda sferica nel nuovo sistema di coordinate, almeno matematicamente; dal punto di vista fisico bisognerà supporre, affinché le considerazioni precedenti abbiano un senso, due mezzi indipendenti nei due sistemi, non interagenti tra loro; in altre parole ogni onda si propaga in un mezzo che si muove assieme alla sorgente che l’ha prodotta, o equivalentemente, con un mezzo che si muove assieme all’osservatore. Rispetto a una tale ipotesi, l’ipotesi della contrazione di Lorentz, comunque assurda, come lo stesso Lorentz riconosce (l’ipotesi era già stata avanzata da Lodge nel 1893 e da Fitzgerald nelle sue lezioni universitarie), sarebbe preferibile alla precedente interpretazione.

Quindi Lorentz è portato a supporre che la contrazione possa essere dovuta all’interazione molecolare e sviluppa la teoria in cui equazioni della stessa forma di quelle di Maxwell vengono attribuite ai singoli elettroni. Ipotizzando, inoltre, che “gli elettroni, i quali allo stato di riposo hanno forma sferica, subiscano, per effetto di una traslazione, una deformazione [a quei tempi si indicava con la quantità che oggi si indica con 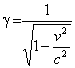], ciascun elemento di volume continuando a conservare la sua carica”; introducendo, necessariamente, la distinzione tra massa trasversale e massa longitudinale, e sollevando irrisolvibili problemi riguardanti la stabilità di un tale modello di elettrone.

Il Poincaré, pur sostenendo l’inevitabilità delle trasformazioni di Voigt, pensava che era necessario introdurre una “forza speciale” che fosse capace, a un tempo, di produrre la contrazione lungo un asse e di mantenere costante le lunghezze lungo gli altri due assi.

La derivazione delle trasformazioni in discussione, effettuata secondo le ipotesi di Einstein, sembrò eliminare tali difficoltà, ma ne sollevò altre, giudicate da molti a quel tempo, ancora più gravi; in quanto, a partire dalle nuove ipotesi, si venivano a rivoluzionare completamente gli usuali concetti di spazio e di tempo.

Notiamo intanto, che se consideriamo la forma di una superficie d’onda, si può eliminare il “mezzo” di propagazione e sostituirlo con il “sistema di riferimento”, senza mutare il significato delle trasformazioni di Voigt.

Infatti immaginiamo due sistemi di riferimento in moto relativo, rettilineo, uniforme lungo un’arbitraria direzione, con velocità v.

Indichiamo con le coordinate di un evento che si produce in A come misurato da A, con , le coordinate dell’evento che si produce in A come misurato da B e, analogamente, per un evento che si produce in B, indichiamo con e le coordinate come misurate da A e B, rispettivamente.

Se assumiamo che all’istante si abbia , con le opportune condizioni iniziali per la velocità, secondo la meccanica classica si hanno le seguenti formule di trasformazione:

, ,

, ,

, .

Le ultime due, a partire da P. Frank, vengono dette “trasformazioni di Galileo”.

Se confondiamo le dette trasformazioni tra loro arriviamo a degli insostenibili paradossi come analizzati dal Perucca.⁹

Consideriamo una sorgente in A capace di sparare proiettili in tutte le direzioni con velocità arbitraria, ma costante in modulo, diciamo c.

Consideriamo il fronte d’onda della nuvola di proiettili sparati al tempo . Vista da A sarà una superficie sferica di equazione:

,

vista da B sarà una superficie ellittica di equazione:

Analogamente per una sorgente posta in B.

In altre parole, se la sorgente si trova nel sistema in cui le misure vengono effettuate appare sferica, se si trova nell’altro sistema, appare ellittica. È irrilevante quale dei due sistemi si voglia ritenere in quiete (notiamo qui che lo spazio in quiete assoluta non è di Newton ma è un’invenzione di Eulero, la fisica di Newton si può mettere in forma “assoluta”, cioè indipendente dal sistema di coordinate e dalle unità di misura, cioè dalle misure relative, sensibili e volgari di Newton, utilizzando il calcolo geometrico di Peano).¹⁰

Ma introducendo la trasformazione di Voigt si può fare in modo che anche A può scrivere l’equazione della superficie sferica per una sorgente in B.

Naturalmente tale superficie sferica non è quella che vedrebbe, effettuando le opportune misure; la trasformazione è solo un artificio formale per cambiare la forma dell’equazione e non la forma del fronte d’onda. Se i proiettili avessero una velocità diversa da c il vantaggio formale verrebbe automaticamente perso, se si volessero mantenere le trasformazioni ricavate con lo stesso valore della precedente velocità.

In tutti gli scrittori di relatività si riscontra l’ambiguità relativa a questa interpretazione delle dette trasformazioni, in certi contesti sembra che si parli della quaterna di numeri , in altri contesti sembra che si parli dell’altra quaterna , come se la trasformazione non fosse più un semplice artificio formale ma riguardasse le effettive misure che i due osservatori compiono. È chiaro che finché nelle formule non intervengono le condizioni iniziali non c’è differenza tra i vari casi, non è più così quando intervengano le condizioni iniziali che sono diverse per i vari casi.

Si potrebbe pensare che se tutte le misure venissero effettuate solo a mezzo di un orologio localmente fissato, vicino a ciascun osservatore, in quiete o in moto che fosse, si potrebbero identificare le trasformazioni con il risultato effettivo delle conseguenti misurazioni (questa è l’ipotesi sostenuta in un noto libro sulla relatività,¹¹ ma vedremo che ciò non risulta vero senza particolari convenzioni sulle unità di misura nei due sistemi); alla fine il Synge si riduce a ipotizzare l’invarianza del quadrintervallo e cerca di dimostrare la possibilità di misurarlo con complicatissime operazioni fisiche che nessun fisico sperimentale si sognerebbe di fare, ammesso che fosse possibile. Si dice che Einstein cercasse la “semplicità”, ma una formula semplice può risolversi in complicatissime operazioni fisiche e viceversa. Occorre scegliere!

La detta ambiguità è manifesta nel famoso articolo di Einstein del 1905, dove essa si accoppia all’altra ambiguità relativa al metodo di misura (cioè a mezzo della luce o per confronto diretto?).

Quindi ci è sembrato opportuno esaminare alcune tra le più note derivazioni delle trasformazioni di Lorentz, per vedere le ipotesi fisiche che si fanno per conseguirle, a partire dalla dimostrazione di Einstein del 1905.

Einstein comincia col fare l’ipotesi che nei due sistemi in moto relativo tra loro “valgano le equazioni meccaniche newtoniane” (nelle riedizioni della Memoria originale aggiunge “È inteso in prima approssimazione”, con questa aggiunta si deve cancellare l’idea che le trasformazioni possano avere validità generale, dal momento che tale ipotesi è essenziale per la sua derivazione!). Poi continua il suo discorso come se intendesse misurare distanze e tempi impiegando esclusivamente segnali luminosi in entrambi i sistemi, assumendo che la luce si propaghi con velocità costante, c, indipendente dal moto della sorgente (questa ipotesi implica l’esistenza dell’“etere”, cioè di un mezzo di propagazione o, in ogni caso un sistema di riferimento in quiete assoluta).

Poi definisce il suo concetto di contemporaneità e assume la linearità delle trasformazioni che cerca.

Nelle deduzioni che vi seguono parla delle trasformazioni tra coordinate come misurate da un osservatore in quiete che osserva un fenomeno che si svolge in un sistema in moto, ma le interpreta come se si trattasse di trasformazioni tra coordinate come misurate nel sistema in moto, chiaramente pensa che non c’è differenza tra i due concetti, cosa che, come abbiamo detto, è vera solo quando non intervengono le velocità.

Considerando un punto sull’asse x, trova la relazione tra tempi e coordinate nei due sistemi.

Poi aggiunge che con lo stesso procedimento si possono trovare le trasformazioni relative alle coordinate di punti che si trovino sugli assi coordinati ortogonali all’asse del moto relativo tra i due sistemi, con ciò noi dobbiamo per forza abbandonare l’idea, che ingenuamente ci eravamo formati che stessimo impiegando solo segnali luminosi, come ipotizza il Synge, infatti in questo caso non potremmo considerare separatamente le tre coordinate di un punto.

Per di più ipotizza che, nelle direzioni normali a quella dell’asse x, la luce “si propaga con la velocità ”, quindi dobbiamo abbandonare l’idea che la luce si propaghi con la stessa velocità in tutte le direzioni. Tale idea potrebbe essere mantenuta solo relativamente a un mezzo di propagazione in quiete o, in ogni caso, in riferimento a un sistema in quiete assoluta, ma tutti ripetono che Einstein ha fatto scomparire l’etere e il sistema in quiete assoluta, nel qual caso la sola ipotesi che si possa sostenere è quella balistica del Ritz, che tuttavia tutti rifiutano in base a ragioni poco chiare, alcuni, come il Levi - Civita, la rigettano a causa del fatto che in moti accelerati si dovrebbero osservare degli effetti che non si osservano nelle stelle doppie, ma se si fanno intervenire moti accelerati le trasformazioni di Lorentz mostrerebbero lo stesso effetto, tuttavia le trasformazioni di Lorentz non sono adeguate per trattare moti accelerati, ricordiamo in proposito il cosiddetto “no - interaction theorem” ¹².

Infine aggiunge un’altra ipotesi, precedentemente non enunciata, cioè la proprietà di gruppo, non leggittima nel caso che distanze e tempi siano tutte misurate con orologi, localmente posti, e con la luce, ipotesi che tuttavia non basta a ottenere le trasformazioni di Lorentz e quindi è costretto a ricorrere ad una fantomatica ipotesi di simmetria, in pratica abbandonando l’idea che si tratti di misure fatte a mezzo della luce e di trasformazioni che si riferiscono a misure fatte dall’uno per eventi nel sistema dell’altro e ancora tacitamente assumendo che le trasformazioni siano le stesse per due sistemi che reciprocamente si avvicinino o si allontanino (questo è un fatto assoluto che non dipende dalla scelta dei segni nel sistema di coordinate).

In un’annotazione aggiunta nelle successive pubblicazioni Einstein nota che le trasformazioni di Lorentz sono più semplicemente deducibili assumendo che in entrambi i sistemi valgano le relazioni r′ ² - c² t′ ² = 0 e r ² - c² t ² = 0 .

Che poi è l’ipotesi che veniva inconsciamente presupposta nella derivazione precedente, invece, delle due ipotesi esplicitamente enunziate, non è stato fatto alcun uso nella derivazione.

A questa nuova ipotesi fa ricorso esplicitamente successivamente.¹³

Dicendo, senza dimostrarlo, che essa si ricava dalle due ipotesi precedenti, esse sono state enunciate esplicitamente nella memoria del 1905, precisamente:

1. Le leggi, secondo le quali si modificano gli stati dei sistemi fisici, sono indipendenti dal fatto che questi cambiamenti di stato vengano riferiti all’uno o all’altro di due sistemi di coordinate che si trovino in relativa reciproca traslazione uniforme.

2. Ogni raggio di luce si muove nel sistema di coordinate “in quiete” con la determinata velocità c, indipendentemente dal fatto che quel raggio di luce sia emesso da un corpo in quiete, o da un corpo in movimento.

Ora la prima ipotesi è sempre vera in meccanica newtoniana (per sistemi in moto relativo traslazionale uniforme), se per leggi fisiche si intendono quelle che coinvolgono le forze e non le velocità, o, senza alcuna restrizione, quelle relative a fenomeni che avvengono nello stesso sistema di riferimento. Non è più così se si usano le trasformazioni di Lorentz, infatti, come abbiamo detto, il fronte d’onda di una nuvola di proiettili con velocità diversa da c, appare sferico per uno dei due osservatori ed ellittico per l’altro, con ciò dobbiamo rinunciare all’ipotesi esplicitamente sostenuta da Einstein di spazi eudidei per entrambi gli osservatori.

In seguito il Minkowski dimostra rigorosamente che condizione necessaria e sufficiente per la validità delle trasformazioni di Lorentz è l’invarianza del quadrintervallo. Riferisce Pais,¹⁴ che, secondo un’informazione ricevuta da Bargmann, Einstein riteneva che la formulazione di Minkowski fosse solo uno sfoggio di “erudizione superflua”.

Quindi dal punto di vista della matematica le cose si possono mettere a posto, ma dal punto di vista della fisica bisogna spiegare da dove deriviamo l’affermazione che il quadrintervallo deve rimanere invariante?

Quindi, negli ulteriori scritti, Einstein abbandona l’idea che le ipotesi di una teoria fisica debbano essere derivate da fatti sperimentali e passa a un nuovo credo epistemologico che battezza col nome di “metodo ipotetico deduttivo”.

Ma molti fisici non vogliono abbandonare l’idea che le ipotesi di una teoria debbano derivarsi dagli esperimenti fisici e cercano altri modi di derivazione ma, come vedremo, spostano semplicemente da un posto ad un altro le contraddizioni.

Gli autori più antichi¹⁵ non si discostano dall’ultima derivazione di Einstein (vedi rif. a nota 13) cioè asseriscono che i due postulati precedenti implicano che ds² = 0 implica ds′ ² = 0 (senza dimostrarlo!) e poi ricorrono al solito argomento della simmetria (?!).

Fra gli autori più recenti alcuni dimostrano che le trasformazioni di Lorentz implicano l’invarianza della ds² = 0 ma si dimenticano di dimostrare che esse siano le uniche¹⁶: si immagina un breve impulso di luce, il cui fronte d’onda è una superficie sferica che si propaga nello spazio; tale impulso viene emesso da una sorgente che, all’istante di emissione t = t′ = 0, si trova alla comune (in quell’istante) origine di due sistemi inerziali, con la stessa direzione e con la stessa orientazione degli assi coordinati, la cui velocità relativa, v, è diretta lungo l’asse x.

Essendo x, y, z, t, e x′, y′, z′, t′, rispettivamente, le coordinate di un generico “evento” come visto nei due sistemi, dai due postulati enunciati si desume (ma ciò non viene dimostrato) che la “forma” del fronte d’onda deve essere la stessa per i due osservatori,¹⁷ quindi

(7) x² + y² + z² - c² t² = 0 e x′ ² + y′ ² + z′ ² - c² t′ ² = 0

Notiamo intanto che le (7) implicano che il fronte d’onda emesso dalla sorgente è sferico in entrambi i sistemi in moto relativo. Questa affermazione non si può ricavare dai due postulati di Einstein.

Poi si asserisce che le trasformazioni di Lorentz:

(8)

con

(9) ,

sono le uniche che verificano le due equazioni (7); la dimostrazione avviene verificando banalmente che le trasformazioni di Lorentz, (8) e (9), di fatto verificano le (7); ma poi ci si dimentica di provare che esse siano davvero le uniche! Al contrario, si può verificare, altrettanto banalmente, che vi sono infinite altre trasformazioni che soddisfano le (7), p. es.:

con a e b funzioni arbitrarie della velocità.

Certamente queste trasformazioni non sono lineari; ma, come vedremo, ve ne sono anche di lineari e diverse, comunque, dalle (8), (9).

Ma prima conviene esaminare le supposte derivazioni di altri autori, largamente diffuse nella didattica della fisica, come quelle che si leggono nel testo di Landau e Lifshitz.¹⁸

Qui, letteralmente, ci si arrampica sugli specchi, come si usa dire:

“Experiments shows that the so-called “principle of relativity” is valid. According to this principle all the laws of nature are identical in all inertial systems of reference. In other words, the equations expressing the laws of nature are invariant with respect to trasformations of coordinates and time from one inertial system to another. This means that the equation describing any law of nature, when written in terms of coordinates and time in different inertial reference systems, has one and the same form”, come si vede, si stanno identificando tre formulazioni semanticamente diverse e, via, via, sempre più deboli, dal punto di vista operativo, per arrivare all’ultima che poi sarà, successivamente, la sola ad essere impiegata formalmente; salvo, poi, a ricorrere alle prime due per l’interpretazione delle formule ottenute. Non crediamo che si possa fare didattica ricorrendo continuamente a cotali slittamenti semantici!

Intanto si usa il termine “interazione” in modo assolutamente ambiguo; infatti (a pag. 1) si dice (la traduzione è nostra): “L’interazione delle particelle materiali viene descritta nella meccanica ordinaria per mezzo di un’energia potenziale di interazione, che appare come una funzione delle coordinate delle particelle interagenti. È facile vedere che questo modo di descrivere le interazioni contiene l’assunzione di una propagazione istantanea delle interazioni. Questo poiché le forze che le particelle esercitano una sull’altra a un particolare istante di tempo dipendono, secondo tale descrizione, solo dalla posizione delle particelle a tale preciso istante. Una variazione nella posizione di una qualunque delle particelle interagenti influenza le altre particelle immediatamente”.

Fin qui si sta parlando dell’interazione in modo da farla coincidere con l’energia potenziale, a parte l’ambiguo significato del termine “influenza” (influences nella versione inglese a cui facciamo riferimento); ma poi si continua: “Tuttavia, l’esperimento mostra che le interazioni istantanee non esistono in natura. Così una meccanica basata sull’assunzione di una propagazione istantanea delle interazioni contiene in se stessa una certa inaccuratezza. In realtà, se si verifica un qualche cambiamento in uno dei corpi interagenti, esso influenzerà gli altri corpi solo dopo un certo lasso di tempo. È solo dopo questo intervallo di tempo che i processi causati dalla variazione iniziale cominceranno a verificarsi nel secondo corpo. Dividendo la distanza tra i due corpi per tale intervallo di tempo, noi otteniamo la velocità di propagazione dell’interazione.”

“Notiamo che questa velocità dovrebbe, strettamente parlando, essere chiamata la massima velocità di propagazione dell’interazione. Essa determina solo l’intervallo di tempo dopo il quale una variazione che si verifica in un corpo comincia a manifestarsi in un altro corpo. ... Le interazioni che si propagano da una particella a un’altra sono spesso chiamate “segnali”, inviati dalla prima particella e che “informano” la seconda particella delle variazioni che la prima ha sperimentato. La velocità di propagazione dell’interazione viene quindi detta la velocità di segnale”.

Ora si sta parlando di un altro e ben diverso concetto di interazione e cioè della “propagazione di un segnale che si manifesta empiricamente” ma si può banalmente vedere che in un modello “newtoniano” di una catena di oscillatori, il segnale si manifesta, sensibilmente, con un ritardo temporale che dipende dalle costanti di interazione e dalle masse degli oscillatori.¹⁹ Riesce difficile capire la necessità di tali mistificazioni didattiche; non è certamente sulla base di tali “esperienze” (?) che si può decidere la validità di una teoria scientifica, specialmente quando raffinati esperimenti, come quello di Michelson e Morley, hanno lasciato nel dubbio molti illustri fisici, sia sperimentali che teorici.

Dopo questa “pseudo-giustificauione”, si scrivono (con simboli leggermente diversi da quelli che qui abbiamo usato) le (7), relativamente, però, a variazioni finite o infinitesime.

Si asserisce quindi che, se la variazione infinitesima del quadrintervallo è nulla per i due osservatori (ds = ds′ = 0, e ciò si deduce, non si sa come, dai due postulati prima enunciati), allora si può, secondo gli autori, dimostrare che deve essere ds = ds′ in ogni caso (cioè anche per ds = ds′ ¹ 0), con un’argomentazione molto speciosa e, ovviamente, falsa, visto che sopra abbiamo dato due esempi, e non sono i soli, in cui il presunto teorema risulta falso.

Ma vediamo ora di capire, se ci sarà possibile, quali siano tutte le ipotesi fisiche che bisogna fare per arrivare alle trasformazioni di Lorentz.

Qualcuno tenta di essere più rigoroso dal punto di vista della matematica, trascurando il rigore semantico. Esamineremo solo la derivazione del Terletski²⁰ che si propone di pervenire alle trasformazioni di Lorentz senza usare il postulato sulla velocità della luce.

Indicando con E un evento, questo ha una realtà fisica assoluta, cioè indipendente da qualunque osservatore, anche se può essere individuato dai vari osservatori inerziali solo mediante due quaterne di numeri diverse: x₁, x₂, x₃, x₄ e x′₁, x′₂, x′₃, x′₄ .

Deve perciò esistere una corrispondenza biunivoca tra le due quaterne:

x′₁ = f₁ (x₁, x₂, x₃, x₄)

x′₂ = f₂ (x₁, x₂, x₃, x₄)

x′₃ = f₃ (x₁, x₂, x₃, x₄)

x′₄ = f₄ (x₁, x₂, x₃, x₄)

che ci deve permettere di passare senza ambiguità dai parametri di un sistema a quelli dell’altro, se l’evento è assoluto.

Usualmente, a partire dallo stesso Einstein, si postula che tali trasformazioni devono essere lineari. Il nostro autore si propone, invece, di dimostrare la linearità a partire da determinate ipotesi fisiche.

Pretenderemo, per qualunque indice i e per due eventi qualsiasi, E_a, E_b, che si possa avere:

l′_i = x′_i,b - x′_i,a

dipendente da

l_j = x_j,b - x_j,a

ma indipendente da x_j,a , per qualunque j; questo corrisponde all’affermazione che, nei due sistemi, le proiezioni sugli assi coordinati della differenza tra due eventi non dipendono dagli estremi, ma solo dalla differenza tra i numeri che individuano tali estremi, cioè dalle lunghezze dei segmenti e degli intervalli di tempo fissate sugli assi (con ciò è praticamente finita la pretesa che si parli solo di eventi e le grandezze prendono il sopravvento); si dovrà avere:

;

questo implica, se assumiamo che l_j non dipende dall’evento che individua un estremo, che:

,

con a_ij indipendente dall’evento e quindi le nostre relazioni sono lineari e il rapporto tra segmenti staccati sugli assi coordinati, relativi a due eventi dati, dipenderà solo dal rapporto tra le unità di misura scelte nei due sistemi; cioè, si può trasportare un segmento o traslare un intervallo temporale senza che ne vari la misura; o, in altre parole, lo spazio è omogeneo e il tempo è uniforme, in entrambi i sistemi, almeno separatamente (ma chi ci assicura che tali proprietà, ovvie per lo spazio e per il tempo assoluti, nel senso newtoniano del termine (e ciò per la stessa definizione di grandezza fisica), debbano continuare a valere anche quando, per ottenere una qualsiasi misura, saremo costretti a frapporre la propagazione luminosa? Quindi le relazioni implicano delle ipotesi ben precise e determinate sul comportamento della luce).

Naturalmente vale anche la proposizione inversa, cioè se lo spazio è omogeneo ed il tempo è uniforme, allora le nostre relazioni devono essere lineari, per cui possiamo affermare che: se nei due sistemi, separatamente considerati, lo spazio è omogeneo ed il tempo è uniforme, allora le relazioni che legano i rispettivi parametri avranno la forma

,

con i coefficienti che possono solo dipendere dalla velocità relativa tra i due sistemi. Tali relazioni tra eventi non sono “lineari” secondo la definizione matematica, ma le si possono far diventare.

Infatti, se lo spazio è omogeneo ed il tempo è uniforme, siamo autorizzati a scegliere arbitrariamente l’origine degli assi e quindi porre a_i0 = 0 per ogni i, con ciò realizzando anche la proprietà matematica della linearità delle relazioni, che è propria delle trasformazioni di Lorentz.

Un’altra proprietà che il nostro autore presuppone, anch’essa propria delle trasformazioni di Lorentz, è l’isotropia dello spazio, per entrambi i sistemi; questo permette l’arbitraria orientazione dei tre assi spaziali, e, anche, implica che gli assi coordinati dell’un sistema si possono far coincidere con quelli dell’altro, e deve aversi per i,j = 1,2,3, a_ij = 0 per i ¹ j, e anche a_2,4 = a_3,4 = a_4,2 = a_4,3 = 0 , quindi:

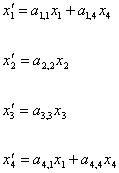
D’altra parte, poiché per x′ = 0 la relazione tra x e t rappresenta il moto, x = vt, dell’origine dell’altro sistema, e, ancora, supponendo la stessa unità di misura per gli assi x′ e y′ , possiamo scrivere:

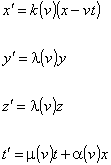
A questo punto il nostro autore si inventa un postulato falso asserendo che “L’isotropia dello spazio anche implica la sua simmetria” e ragiona così:

Supponiamo di invertire l’orientazione dell’asse x′, affinché la situazione fisica rimanga immutata, deve cambiare il segno di v (questa pretesa è piuttoso strana, poiché v è la velocità relativa dei due osservatori e per un valore di x assegnato, il suo segno indica solo se i due sistemi si allontanino o si avvicinino reciprocamente e non può cambiare invertendo l’asse x) quindi:

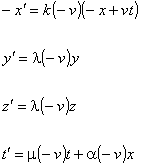
(L’autore anche dimentica che con tale operazione si cambia l’orientazione della terna di riferimento, e quindi bisogna porre anche: o (esclusivo) ) .

Quindi confronta con le precedenti e verifica che sono funzioni simmetriche in v e, invece, è antisimmetrica.

Introducendo la funzione simmetrica , le equazioni diventano:

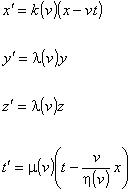
Notiamo a questo punto che se poniamo , , con una funzione arbitraria della velocità e come data nella (9), si otterrebbe:

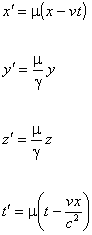
Queste trasformazioni lineari, diverse dalle trasformazioni di Lorentz, obbediscono tuttavia alle (7).

A questo punto il nostro autore impone la condizione che le trasformazioni, che indicheremo con L, formino gruppo e, quindi, in particolare, deve aversi L(-v) = L^-1 (v), e ragiona così:

“La trasformazione inversa deve solo differire nel segno della velocità v (?!), poiché il sistema Σ′ si muove con velocità v verso destra relativamente al sistema Σ, mentre il sistema Σ si muove verso sinistra relativamente al sistema Σ′ con velocità -v (quando quest’ultimo si consideri in quiete). Conseguentemente, la trasformazione inversa deve essere della forma”:

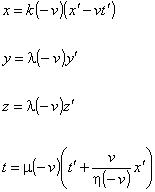
Confrontando con le precedenti trova che deve valere:

(***) .

Ma vediamo che cosa implica fisicamente la (***), che poi è, anche, l’ipotesi aggiuntiva di Einstein, che sopra abbiamo menzionato e che Einstein si limita a giustificare ricorrendo a problematiche “ragioni di simmetria”.

Dalle analisi di Terletskii vediamo che essa viene dall’ipotesi che le trasformazioni formino un gruppo moltiplicativo.

Considerando tre osservatori con diverse velocità, l’ipotesi di gruppo implica, come facilmente si prova:

quindi lo stesso valore per qualsiasi sistema di riferimento e con le dimensioni di una velocità al quadrato, da determinare empiricamente (per tale determinazione l’autore pensa alla relazione, che crede “empirica”, ).

Si ottiene: .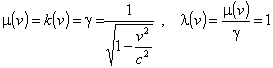

L’ipotesi di gruppo ha come conseguenza che le velocità relative non possono essere additive, per cui si usa chiamare “addizione”, l’operazione:

.

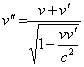Dall’ipotesi di gruppo deriva anche la proprietà di simmetria, se il terzo osservatore ha

velocità -v ed è sincronizzato in modo che anche per esso si abbia x″ = y″ = z″ = 0 e t″ = 0 per x = y = z = t = 0.

Si ha:

,

e se si suppone che l″ = l (non si vede, per questa ulteriore ipotesi, alcuna ragione di ordine logico, cioè tale che si possa derivare da precedenti assiomi) e quindi:

.

Quest’ultima ipotesi, oltre a non avere alcuna ragione di ordine logico, è contraddetta da tutte le esperienze che si fanno sulla propagazione ondosa nei mezzi elastici.

E, ancora, non si potrebbe più capire come mai il fatto che i sistemi si avvicinino o si allontanino, reciprocamente, non debba avere alcuna influenza sui fenomeni fisici; ci si chiede, allora, che cosa mai può avere a che fare la “propagazione” della luce con le trasformazioni di Lorentz; al massimo la costante c, che vi compare, può solo essere la costante di Maxwell , che è una proprietà dello spazio vuoto indipendente da qualsiasi propagazione, tant’è che si misura staticamente; tale fondamentale obiezione è stata ripetutamente avanzata da molti.

Infatti, nel modello delle misure effettuate con segnalazioni luminose, come vedremo, non vale la proprietà di gruppo, che è una richiesta molto più forte del principio di relatività, la ragione sta nel fatto che, assumendo la luce come segnale di campionamento dei due sistemi, le trasformazioni devono essere interpretate come l’invio di segnali da O a O′, da O′ a O″ e da O″ a O, quindi il percorso da O″ a O è un lato del triangolo OO′O″, che è minore degli altri due lati, nonostante la diversa contemporaneità dei riferimenti. La proprietà di gruppo varrà solo se i tre punti sono allineati.

Mostreremo ora come si possa arrivare alle trasformazioni di Lorentz, a partire dalle ipotesi di Einstein (esplicite ed implicite), usando formalmente il calcolo delle grandezze.

Svilupperemo la particolare interpretazione della teoria della relatività (ristretta) proposta da Synge e da questi esposta con la usuale confusione tra grandezze e numeri,²¹ che, se va bene per la fisica classica, è assolutamente pericolosa nella fisica relativistica quando si voglia stabilire il significato fisico delle trasformazioni di Lorentz, fatto che è confermato dalle infinite proposte interpretative avanzate nel passato e che si continuano ad avanzare perennemente.

Converremo di usare le lettere maiuscole per indicare le grandezze, le corrispettive lettere minuscole per indicare le relative misure e le lettere minuscole con un apice per indicare le rispettive unità di misura.

Useremo le lettere segnate con ′ per le quantità che si riferiscono al sistema in moto, per distinguerle dalle corrispondenti quantità nel sistema in quiete.

Supponiamo che i due osservatori O e O′, di cui parla Einstein, scelgano la stessa origine delle coordinate al tempo t′ = t = 0 e decidano entrambi di usare la luce per misurare le distanze ognuno nel proprio sistema.

Per quanto si legge nell’articolo di Einstein del 1905, possiamo dedurre che ognuno dei due osservatori può immaginare di avere a che fare con spazi e tempi assoluti (ipotesi necessaria se si pretende che i due osservatori possano fare misure per confronto diretto, ognuno all’interno del proprio sistema; questa assunzione verrà, in seguito, abbandonata dallo stesso Einstein perché, come vedremo subito, è incompatibile con le trasformazioni di Lorentz, quando non si vogliano fare ipotesi inaccettabili e se si vuole mantenere alla teoria il suo ruolo di “teoria fisica” e non quello, puramente estetico, di riscrittura delle equazioni della meccanica).

Per l’ipotesi della relatività, come formulata nella 1., basterà considerare solo quello che può dedurre il primo osservatore, in quanto il secondo ragionerà esattamente allo stesso modo.

Useremo l’aggettivo “assoluto” nel senso newtoniano e cioè quello definito da regoli rigidi, che si possono trasportare e di tempo uniforme e indipendente dallo spazio. Non supporremo, però, l’esistenza di uno spazio assoluto in “quiete assoluta”..

Sia P la posizione (“assoluta”) al tempo T (“assoluto”) di una particella materiale secondo il primo osservatore. Sia O l’origine delle sue coordinate ed O′ la posizione dell’origine delle coordinate del secondo osservatore, come vista dal primo osservatore.

Per il primo osservatore, dal momento che il suo spazio è eudideo e che tempi e distanze sono misurate con operazioni indipendenti, si ha:

P - O = P - O′ + O′ - O.

Se poniamo:

(10) R = P - O ; R′ = P - O′ ; VT = O′ - O ;

possiamo scrivere:

(11) R′ = R - VT.

Siamo ora R e T le coordinate (spaziali e temporali) di un evento dato per O.

Supponiamo che all’istante opportuno T_p , O lanci un segnale luminoso verso R. Sarà ricevuto al tempo (avendo posto R = |R| e C = |C| ). Sarà di ritorno al tempo .

Calcolerà:

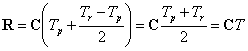
Secondo le vedute di O, affinché O possa ricevere propriamente il segnale di ritorno, O′ dovrà lanciare il segnale al tempo T₁, istante in cui si troverà in una certa posizione R₁, tale che il segnale possa giungere in R al tempo

(12)

ed essere ricevuto di ritorno da O, al tempo

(13) ,

essendo R₂ la posizione di O′ al tempo T₂.

R₁, R₂, T₁, T₂ si intendono tutte misurate nel riferimento di O.

Per trovare più semplicemente le relazioni opportune tra le varie grandezze poniamo:

(14)

Naturalmente si ha:

(15) R = CT , R₁ = VT₁ , R₂ = VT₂.

Da (12), (13), (14) si ha:

(16) T = T₁ + |A| T = T₂ - |B|

(notiamo che per O l’intervallo di tempo impiegato dal segnale per andare da O′ a R è diverso dal tempo impiegato per ritornare in O′, il primo intervallo sarà maggiore o minore del secondo a seconda che O e O′ si allontanino o si avvicinino reciprocamente).

Avendo posto:

(17) ,

per somma e sottrazione delle due equazioni in (16), si ottiene:

(18) 2( T - T′ ) = |A| - |B| = D

(19) T₂ - T₁ = |A| + |B| = S .

Dalle definizioni di D ed S si trova:

(20)

e ancora, tenuto conto delle definizioni precedenti:

(21)

da cui

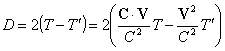
e, quindi, anche:

.

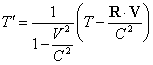Se usiamo le stesse unità di misura per misurare V e C, si avrà: e quindi:

(22) .

Per il principio di relatività, O immagina che il secondo osservatore scriverà

(23) R′ = C′ T′ .

La (23), per la (22), può scriversi:

(24)

ricordando che per (11), (15), (23) si ha

C′ T′ = R - V T

e quindi

per cui la (24) si può scrivere:

(25)

Le formule precedenti, per il modo in cui sono state ricavate, obbediscono ai due postulati di Einstein e alla sua definizione di contemporaneità.

Vediamo se i due osservatori possono scegliere unità di misura tali da ottenere le trasformazioni di Lorentz.

Sostituendo alle grandezze le loro espressioni in termini di valori e di unità di misura e ponendo (come è necessario per non violare il principio di relatività): e ; e ponendo, ancora, , vediamo quali ipotesi ulteriori dobbiamo fare per scrivere le trasformazioni di Lorentz relative alle quantità numeriche.

Le (25),(22) diventano:

(26)

(27)

se poniamo, per convenzione otteniamo

e, infine, avremo:

(28)

(29) .

Queste non sono esattamente le trasformazioni di Lorentz, infatti, quando si sceglie per entrambi i sistemi, l’asse x come direzione della velocità relativa si ottiene:

(+)

invece di

(++) .

Ma le formule usuali (più corrette?! — se si pretende c = c′, esse impongono ) si possono facilmente ottenere cambiando leggermente le convenzioni, decidendo di scegliere, nella direzione del moto, unità di misura diverse da quelle di tutte le altre direzioni, arrivando alle formule usuali:²²

(30)

(31) .

Notiamo che con la scelta delle unità cli misura che portano alla (+) non vale la proposizione r′ ² - c² t′ = r ² - c² t , né vale la meno restrittiva (r′ ² - c′ ² t′ = 0) = (r ² - c² t = 0) da cui parte Einstein, ma resta fermo il fatto che per entrambi i sistemi la velocità della luce è costante e indipendente dal moto della sorgente in accordo con le 1. e 2. di Einstein. L’accordo tra i numeri non è verificabile in principio, come si è detto, e, quindi, al di fuori della fisica e dipende solo da molto particolari convenzioni, come abbiamo visto.

Infatti, in linea di principio, non abbiamo alcun modo di verificare le convenzioni che abbiamo fatto sulle unità di misura, perché riguardano un impossibile confronto diretto tra due sistemi in movimento relativo. In teoria, potremmo verificare la coincidenza, anche per osservatori in moto qualsiasi, tra spazio tattile e spazio ottico (ma questo è un altro problema che non ha niente a che vedere con il primo che, come abbiamo detto, non è verificabile per sua natura). Si ritiene che l’esperimento di Michelson e Morley abbia deciso questa questione. Ma molti in passato hanno contestato il risultato dell’esperimento, alcuni contestandone l’accuratezza dal punto di vista sperimentale, altri contestando la teoria dell’apparato, usata per predire il risultato dell’esperimento. A parte il fatto che nell’esperimento effettuato sorgente e rivelatore stanno nello stesso sistema e quindi secondo la meccanica classica, abolito l’etere, si deve ottenere il risultato nullo come di fatto trovato.

L’impressione che si ricava, leggendo la letteratura odierna sull’argomento, è che l’accordo tra teoria ed esperimento sembra essere diventato solo una questione di fede.

Ma, in ogni caso, l’esperimento di cui sopra, quando interpretato come una prova della coincidenza dei due spazi, non cambia niente sulle convenzioni riguardo alle unità di misura, che bisognerà sempre fare; al massimo, può solo dire che non esiste un osservatore privilegiato.

Ecco perché, in seguito, Einstein (dopo la formulazione puramente “geometrica” di Minkovski) abbandona ogni riferimento alle diverse operazioni di misura nei due sistemi di riferimento e si limita a postulare l’invarianza del quadrintervallo, del quale non v’è alcun cenno nel primo articolo. Successivamente è costretto ad asserire:²³ “Né il punto dello spazio, né l’istante del tempo in cui qualcosa accade, hanno una realtà fisica, ma soltanto l’evento in se stesso. Non vi è alcuna relazione spaziale assoluta, cioè indipendente dallo spazio di riferimento, né alcuna relazione temporale assoluta tra due eventi, ma vi è soltanto una relazione assoluta nello spazio e nel tempo, cioè indipendente dallo spazio di riferimento, come apparirà nel seguito.”

La teoria della relatività ristretta viene oggi largamente applicata in tutte le teorie fisiche moderne, dalle teorie della fisica degli stati aggregati, alla fisica nucleare, dalla fisica della rivelazione della radiazione elettromagnetica, alla fisica delle particelle elementari.

Naturalmente si tratta sempre di confrontare determinate formule, ricavate da modelli idealizzati su situazioni fisiche reali estremamente complicate, con i risultati sperimentali. Notevoli sono state le discussioni che si sono avute sul famoso esperimento di Michelson e Morley; ma discorsi analoghi si potrebbero fare su qualsiasi altro esperimento, anche se oggi tali discorsi non vengono più fatti. Quindi, il fatto che le formule ricavate si accordino con gli esperimenti non costituisce una prova della validità fisica della teoria matematica, ma solo prova che essa riesce a dar conto di certi risultati. La validità di una teoria fisica può asserirsi solo in contrapposto alle previsioni di un’altra teoria alternativa.

Questo fatto banale, spesso messo in evidenza da qualche epistemologo intelligente, viene sistematicamente dimenticato, per cui in ogni libro che parli della relatività ristretta si può leggere che, se anche si possano avere dubbi sulla relatività generale, quella particolare è largamente confermata sperimentalmente.

Ma quando si fa un minimo sforzo per convalidare tale asserzione, andando solo un pochino oltre la semplice enunciazione categorica dell’asserto, si scopre che le cose non stanno per niente così.

Esaminiamo alcuni recenti articoli sulla questione.²⁴

Il Mac Arthur comincia col ricordare che diverse alternative alla relatività speciale, in quanto fondata sulle trasformazioni di Lorentz, sono state avanzate, anche recentemente, con un grado maggiore o minore di generalità, ma che tutte danno, con le opportune restrizioni aggiuntive, le trasformazioni di Lorentz.

A suo giudizio si tratterebbe di valutare la sensibilità di tutti gli esperimenti che oggi vengono considerati come i più decisivi per la conferma delle trasformazioni di Lorentz, e procede in tale valutazione per ogni singolo esperimento. Ma, stranamente, qui si ferma, senza dire se i risultati degli esperimenti siano discriminanti in base alle sensibilità da lui calcolate, limitandosi ad avvertire il lettore che un tale confronto è già stato fatto da Maciel e Tiomno, senza nemmeno dare un giudizio su tali confronti ai quali si riferisce. Questa voluta “neutralità” di giudizio della deontologia moderna, a nostro giudizio, è l’aspetto più negativo e denota semplicemente la paura di compromettersi nei confronti del paradigma dominante.

Nello stesso tempo gli scienziati moderni sono sempre pronti a scagliare vituperi contro il lisenkismo, imperante in URSS nei giorni bui dello stalinismo.

Andando a leggere l’articolo a cui fa riferimento si scopre che nessuno degli esperimenti, ritenuti i più significativi, è discriminante nei confronti delle formule più generali, tranne uno che, però, è in disaccordo con le trasformazioni di Lorentz.

Non entreremo nei dettagli di tali esperimenti, anche perché non è facile confrontare il modello matematico con la reale situazione fisica dell’esperimento, nota, solo in parte, agli stessi sperimentatori e quasi del tutto ignota ai lettori dell’articolo, solo gli sperimentali, specialisti del campo, possono riuscire a capirne un po’ di più; comunque chi è interessato può ricostruire, in parte, il significato dei singoli esperimenti attraverso la bibliografia citata dagli autori di cui a nota 24.

Abbiamo visto che le condizioni di linearità e di indipendenza tra gli assi coordinati comportano l’omogeneità e l’isotropia dello spazio; quindi, un esperimento che voglia provare la validità delle trasformazioni di Lorentz deve assicurarsi che l’esperimento sia effettivamente isolato da influenze esterne e che il sistema di riferimento (in teoria il sistema delle stelle fisse, ma in pratica il laboratorio terrestre, spesso non corretto per l’effetto della sua rotazione, assunta a priori come trascurabile) si possa considerare come fisso, tale da non introdurre forze inerziali del tipo della forza di Coriolis.

Un disaccordo trovato con le cosiddette trasformazioni di Galileo non falsifica la meccanica di Newton, ma dice semplicemente che il modello ideale matematico, con cui si confrontano i dati sperimentali, non è adeguato, come del resto è stato messo in chiara evidenza dagli esperimenti di Miller, oggi totalmente dimenticati.

In questo contesto c’è da osservare, come è stato notato recentemente,²⁵ cioè ottantanni dopo la memoria di Einstein, che non è affatto vera l’affermazione riportata in quasi tutti i libri, che le trasformazioni di Lorentz si riducano a quelle di Galileo per β << 1. Per accorgersi di questo basta osservare che dalle trasformazioni di Lorentz per β ® 0 si ha e ; e quest’ultima, per Δ x sufficientemente grande, è diversa dalla condizione Δ t = Δ t′ pretesa dalle trasformazioni di Galileo; tale fatto, che fra l’altro implica che si possono avere sistemi einsteiniani con tempi galileiani e viceversa, è rilevante per qualsiasi confronto della teoria con gli esperimenti.

Accertatisi che l’esperimento esclude la fisica newtoniana, quindi, ci sarà ancora da confrontarsi con le ipotesi di Einstein della memoria del 1905, che hanno un preciso significato fisico operativo e una loro validità teorica ben precisa, indipendentemente da qualunque possibile conferma sperimentale.

Sfortunatamente, come abbiamo visto e come da altri, in passato, è stato notato, tali ipotesi non implicano le trasformazioni di Lorentz.

Le dette ipotesi conducono a trasformazioni più generali di quelle di Lorentz. L’ipotesi della particolare sincronizzazione degli orologi, secondo il metodo di Einstein, restringe ancora la classe delle possibili trasformazioni basate solo sulle ipotesi precedenti, tuttavia ancora non conduce alle trasformazioni di Lorentz.

Tale sincronizzazione, o altra alternativa, è una necessità, quando non si conosca niente sull’eventuale moto assoluto della terra, ma non esclude tale moto assoluto, e non è generale, in quanto entra in gioco solo quando siamo costretti a misurare distanze tra punti usando la luce, perché impossibilitati a fare misure per confronto diretto, e non può essere assunta l’equivalenza operativa tra i due generi di misure aprioristicamente, introducendola fin da principio nel modello matematico, quando è proprio quello che si vuole verificare sperimentalmente.

Ciò è contrario a qualunque deontologia scientifica. E solo quando si saranno verificate, una ad una, le varie ipotesi, solo se esse non riescono a spiegare il risultato sperimentale e si verifica, invece, che il risultato è spiegato dalle trasformazioni di Lorentz, prese insieme alla filosofia ad esse associata, si potrà dire che la teoria della relatività ristretta, come oggi la conosciamo, è stata confermata o, per meglio dire, non è stata falsificata da quegli esperimenti che invece falsificano le teorie alternative.

Purtroppo, se si volesse stare alle conclusioni di Maciel e Tiomno, sembrerebbe proprio il contrario, ma la questione meriterebbe di essere indagata ulteriormente.

Purtroppo nessuno sembra avvertire tale necessità; perché, a causa della massificazione della ricerca scientifica avutasi nell’ultimo cinquantennio, lo scopo dei ricercatori non sembra più quello di trovare la spiegazione delle leggi empiriche, ma solo quello di avere delle formule con le quali giocare in un’assurda competizione a chi gioca meglio.

NOTE

1  K. Marx, Democrito e Epicuro, dissertazione dottorale in appendice al libro di A. Sabetti, Sulla fondazione del materialismo storico, La Nuova Italia, Firenze, 1962. TORNA

2 Cicerone, De Fin. I 6, 20. TORNA

3  Vedi E. Perucca, Fisica Generale e Sperimentale, UTET, cfr. anche G. Peano, Operazioni sulle grandezze, in Opere Scelte di G. Peano, a cura di U. Cassina, vol. III, p. 435 e segg. TORNA

4 R. P. Feynman, The Feynman Lectures on Physics, Addison Wesley, 1966, I,1,16,3. TORNA

5  W. Voigt, Über das Doppler’sche Princip, Nachrichten der Königliche Gesellschaft der Wissenschaften zu Göttingen, 10 März 1887. TORNA

6  H. A. Lorentz, The theory of electrons, Teubner, 1909, p. 198. Lorentz ricorda che dopo avere trovata la trasformazione ha saputo che era già stata trovata dal Voigt. TORNA

7  V. Somigliana, Sulla trasformazione di Lorentz, Rend. Acc. dei Lincei, 1° Sem. 1922. TORNA

8 C. Burali - Forti, T. Boggio, Espaces courbes Critique de la relativité, Sten, p. 204 e sg., 1924. TORNA

9  E. Perucca, Fisica Generale e Sperimentale, UTET, 1949, p. 261. TORNA

10 Cfr. S. Notarrigo, Appunti di Fisica Superiore, non pubblicati. TORNA

11 J.L. Synge, Relativity, The special theory, North-Holland P. C., 1956. TORNA

12 H. Van Dam, E. P. Wigner, Phys. Rev., 142, 838, 1966 e H. Leutwyler, Nuovo Cimento,

37,556, 1965. TORNA

13 A. Einstein, Il significato della relatività, Einaudi, 1955. TORNA

14 A. Paìs, Subtle is the Lord, the Science and the Life of Albert Einstein, Oxford Uni. Press, 1982. TORNA

15 W. Pauli, Teoria della relatività, Boringhieri, 1958. Cfr. anche A. Sommerfeld, Mechanics, Acad. Press, 1964. TORNA

16 Cfr. R. B. Leighton, Principles of modern physics, McGraw-Hill, 1959, p. 5 e segg. TORNA

17 La “forma” di un fronte d’onda è una legge fisica? È chiaro che qui si sfrutta l’ambiguità connessa con le parole con cui l’autore ha enunciato il primo postulato, che ha espresso con le seguenti parole: A properly formulated description of a physical phenomenon can contain no reference, either explicit or implicit, to an absolute speed of traslational motion of the coordinate frame in which the phenomenon ia deacribed.

Nessuno saprà mai che cosa l’autore intenda per una “descrizione propriamente formulata di un fenomeno”, oltre al fatto che l’esempio considerato si debba presumere appartenere a tale classe. Se ci capitasse di avere a che fare con un altro esempio, anche solo leggermente diverso, non potremmo mai sapere se dobbiamo includerlo nella classe oppure no! E, ancora, cos’è mai una “velocità assoluta”? dal momento che v è una velocità relativa, niente ci impedirebbe di pensare che il fronte d’onda possa dipendere da essa; come, del resto, si verifica classicamente! La formulazione di Einstein non è meno ambigua. Con la formulazione di Einsteiu, come sopra riportata, siamo costretti a tornare, ma senza risposta, alla prima domanda, cioè, cos’è mai una “legge” ? la “forma” dell’onda è una legge? Anche il secondo postulato soffre di forti e non irrilevanti ambiguità: cos’è la velocità della luce? è forse la velocità di fase di un onda piana sinusoidale, o la velocità di gruppo dell’impulso immaginato dal Leighton? oppure è la velocità di segnale? o quella di energia? (concetti questi introdotti dagli autori classici che si sono occupati, con grande competenza e rigore, della propagazione ondosa nei mezzi elastici) o è semplicemente il numero che compare nelle equazioni di Maxwell? Tutti questi concetti si possono chiamare, e difatti vengono chiamati, “velocità della luce” e sono tutti concetti diversi tra loro, anche numericamente! Non lo sapremo mai, quindi è inutile indagare ulteriormente; assumeremo, perciò, secondo l’andazzo generale, che ognuno è libero di scegliersi il concetto che più gli piace. È chiaro, però, che non potremo fare uso, in questo caso, di nessun sistema deduttivo come definito dal Peano! E si capisce perché quest’ultimo si rifiutava di capire la relatività! TORNA

18 L. Landau, E. Lifshitz, The classical theory of fields, Addison - Wesley, 1951, p. 1 e seg. TORNA

19 Sulla velocità di segnale in sistemi meccanici newtoniani si vedano i lavori di Brillouin e di Sommerfeld in L. Brillouin, Wave propagation and group velocity, Academic Press, 1960, si veda, anche, L. Brillouin, Wave propagation in periodic structures, McGraw-Hill, 1946. TORNA

20 Cnf. Y. P. Terletskii, Paradoxes in the theory of relativity, Plenum Press, 1968. TORNA

21 Vedi rif. a nota 11. Del resto tale interpretazione si può ricavare dalle stesse parole di Einstein: “Siano dati nello spazio in “quiete” due sistemi di coordinate, ossia due sistemi ciascuno di tre rigide linee materiali uscenti da un punto. Gli assi X dei due sistemi coincidano, i loro assi Y e Z siano paralleli. A ogni sistema sia data un’asta di misura e un certo numero di orologi e siano le due aste di misura come pure tutti gli orologi dei due sistemi gli uni agli altri uguali”. In successivi lavori si precisa che con un “certo numero di orologi” si intende uno per ogni punto dello spazio del sistema in moto. La differenza con l’interpretazione di Synge consiste nel fatto che questi presuppone un unico metodo di confronto mediante segnali luminosi, mentre Einstein sembra pensare che all’interno di ciascun sistema i due metodi di misura debbano dare lo stesso risultato, in ogni sistema, questa è un’ipotesi, in linea di principio verificabile, ma praticamente impossibile da verificare. TORNA

22 Cfr. W. Pauli, Teoria della relatività, Boringhieri, 1958, p. 18. TORNA

23 Cfr. Il significato della relatività, op. cit. TORNA

24 Vedi D. W. Mac Arthur, Special relativity: Understanding experimental tests and formulation, Phys. Rev. A, 33 (1986)1 e A. K. A. Maciel, J. Tiomno, Experiments to detect possible weak violation of special relativity, Phys. Rev. Letters, 55(1985),143. TORNA

25 S. K. Ghosal, K. K. Nandi, P. Chakraborty, Passage from einstenian to galileian relatvity and clock syncrony, Z. Naturforsch., 46 a(1991)256. TORNA