Pre-print
a cura degli autori. Originale pubblicato su:
Quaderni
di Storia della Fisica – Giornale di Fisica – 2 – 1997 – pp. 101-110
Ed.
Compositori Bologna, 1997
Riesame della
teoria di Augusto Righi sull’apparato
dell’esperimento di
Michelson e Morley.
P. Di Mauro, S. Notarrigo e A. Pagano
Dipartimento di Fisica dell’Università - Catania
L’esperimento di Michelson e Morley viene spesso presentato come un classico esempio di esperimento cruciale che è servito a discriminare fra la teoria newtoniana e la teoria relativistica einsteiniana.
Di fatto le motivazioni che portarono al progetto dell’esperimento furono ben altre e quando esso fu realizzato la relatività doveva ancora nascere [1].
L’occasione nacque con la messa a punto di un sensibile interferometro da parte di A. A. Michelson; la motivazione, come lo stesso riferisce nell’articolo del suo primo esperimento [2], nasceva da una nota di Maxwell alla voce Etere dell’Enciclopedia Britannica in cui s’immaginava di poter congegnare un esperimento terrestre capace di misurare la velocità relativa del moto di un pianeta rispetto all’etere; Maxwell pensava a un satellite di Giove, anche se riteneva praticamente impossibile l’attuazione di un tale esperimento.
La grande sensibilità dell’interferometro di Michelson avrebbe consentito una misura della velocità del moto orbitale della Terra rispetto all’etere supponendolo in quiete rispetto al sistema solare.
L’idea apparentemente era molto semplice: si divida un fascio di luce a mezzo di una lastra semiargentata, posta a 45° rispetto al fascio incidente, in due componenti, una parallela alla velocità orbitale della Terra, l’altra in direzione ortogonale. I due fasci successivamente riflessi da appositi specchi, a e b, incontrandosi di nuovo dovevano interferire formando delle frange da osservare con apposito cannocchiale.
Ruotando tutto l’apparato di 90° si sarebbe dovuto osservare uno spostamento delle frange d’interferenza.
Il primo esperimento, di cui alla nota precedente, fu cominciato da Michelson a Berlino, ma successivamente fu condotto a termine a Potsdam dal momento che il traffico cittadino turbava notevolmente le misure, data l’estrema sensibilità dell’interferometro; anche lievissime variazioni di temperatura provocavano un effetto molto maggiore dell’effetto che si intendeva misurare.
I calcoli fatti da Michelson, nell’ipotesi che il sistema solare fosse in quiete rispetto all’etere, prevedevano uno spostamento di 0.08 prendendo come unità di misura l’intervallo tra due frange successive.
Il risultato dell’esperimento, tenuto conto delle incertezze sperimentali, dava un valore compreso tra 0.004 e 0.015.
Per cui Michelson concludeva che il risultato si poteva considerare come nullo e che quindi doveva considerarsi erronea l’ipotesi di un etere stazionario, naturalmente rispetto al sistema solare.
Tuttavia la teoria dell’apparato era molto rozza e già Potier metteva in evidenza un errore che quando corretto avrebbe ridotto a 0.04 il valore calcolato, mettendo in crisi le conclusioni di Michelson, date le notevoli incertezze sperimentali.
Michelson e Morley riconoscono la validità dell’osservazione di Potier in un secondo esperimento condotto a Cleveland (Ohio) [3].
Il risultato del nuovo esperimento dava un valore di 0.01 da confrontare con il valore teorico di 0.4 sempre in riferimento all’intervallo tra frange successive, calcolato per la nuova disposizione sperimentale e tenendo conto dell’osservazione di Potier.
Pure questo risultato viene interpretato come nullo anche se il valore trovato era al disopra dello zero entro gli stimati errori sperimentali.
Ma altre critiche venivano mosse alla teoria dell’apparato, tutte basate sostanzialmente sul fatto che non si poteva trattare un singolo raggio di luce come una particella ma bisognava tenere conto del moto effettivo del fronte d’onda.
Infatti Sutherland [4] notava che, nel modello dell’apparato usato da Michelson e Morley, dove s’ipotizzava che i due fasci di luce incidessero normalmemente ai due specchi che dovevano rinviarli indietro per farli interferire, l’interferometro avrebbe dovuto fornire due immagini parallele per cui non si dovevano osservare frange diritte e parallele ma solo frange circolari e che il variare la distanza fra le due immagini avrebbe solo comportato un movimento relativo fra tali frange circolari. Suggeriva inoltre che disallineando leggermente uno degli specchi sarebbe stato possibile osservare lo spostamento nelle migliori condizioni sperimentali.
Lo stesso tipo di obbiezioni vengono mosse da Hicks [5] il quale costruisce una teoria generale dell’apparato con arbitrarie orientazioni degli specchi. Egli aggiunge delle considerazioni erronee su1l’effetto che avrebbe dovuto esercitare la supposta contrazione di FitzGerald-Lorentz. L’erroneità di tali considerazioni veniva ammessa dallo stesso Hicks, ma ciò gettò il discredito su tutta la teoria, la correttezza della quale veniva invece riconosciuta da Morley e Miller [6], i quali si affrettavano a far notare che entro le approssimazioni da loro fatte il loro risultato era corretto, sorvolando sul fatto che proprio l’approssimazione era in questione.
In séguito, con l’affermarsi della teoria della relatività, il supposto risultato nullo dell’esperimento di Michelson e Morley veniva preso come prova definitiva in favore di tale teoria e non si badò più alle critiche di Sutherland e Hicks. Critiche che venivano accomunate alle molte critiche, spesso anche senza fondamento razionale, che venivano mosse alla teoria di Einstein.
Tuttavia la questione fu ripresa da Augusto Righi in quattro successive memorie lette alla Reale Accademia di Bologna [7].
Righi si propone di affrontare la teoria dell’apparato ricorrendo al principio di Huygens.
Egli usa la costruzione di Huygens per mostrare che il movimento del riflettore comporta un’apparente deviazione della direzione del riflettore stesso e costruisce la sua teoria dell’apparato a partire da tale deviazione; in altre parole, avendo trovato tale angolo apparente di deviazione dei riflettori, dovuto al loro movimento rispetto all’etere, pensa che l’apparato reale possa essere sostituito da un apparato ideale in cui l’orientazione dei riflettori venga modificata tenendo conto di tale deviazione angolare e quindi si possa operare come se i riflettori di tale apparato ideale fossero fermi rispetto all’etere.
Portando avanti tali idee nelle sue quattro memorie arriva alla seguenti conclusioni:
1) Nel modello di Michelson e Morley, con specchi perfettamente allineati, non è possibile osservare lo spostamento in quanto l’intervallo fra le frange successive verrebbe ad essere eccessivamente grande, praticamente infinito.
2) Per ridurre l’intervallo fra le frange bisogna disallineare uno degli specchi. L’intervallo tra le frange dipende sensibilmente da tale angolo di disallineamento.
In base a tali conclusioni propone che l’esperimento venga ripetuto e dà la formula dello spostamento solo per i casi in cui il fascio di luce proveniente dalla sorgente sia parallelo od ortogonale alla direzione della velocità orbitale della Terra.
Questo lavoro di Righi è stato preso in esame solo da pochissime persone.
A parte un articolo elogiativo di Dalla Noce [8] in cui correttamente si riassume il lavoro di Righi, citiamo due note di Villey [9] e due lavori di Valle [10].
Questi due autori accettano e lodano l’idea di sostituire l’apparato in moto con quello fermo ma dissentono, tuttavia, in disaccordo anche tra loro, su come trattare il movimento dei raggi di luce nel nuovo apparato, giungendo a conclusioni molto diverse tra loro.
Per cui abbiamo pensato di ripetere i calcoli con un altro procedimento.
Noi pensiamo che sia proprio l’idea di sostituire un apparato fermo ad uno in moto la causa di tali diverse interpretazioni. Fortunatamente il principio di Huygens, una volta accettato (ma non vediamo come lo si possa sostituire), permette di seguire i singoli raggi nel loro percorso, per cui noi, nel séguito, per esaminare la questione, ci atterremo a tale metodo.
Infatti il principio di Huygens implica che i singoli raggi, incontrando un riflettore in moto, si comportino come se, all’istante dell’incontro, il riflettore fosse fermo nel sistema dell’etere (con il termine «sistema dell’etere» intenderemo quel sistema di riferimento nel quale viene definita la velocità della luce nel vuoto, indipendentemente dal fatto che l’etere esista o meno come sostanza).
Questa ipotesi
è ovviamente coerente con l’ipotesi che la luce si propaghi nel sistema dell’etere indipendentemente dal
moto dei corpi e, nel nostro caso, indipendentemente dal moto del riflettore,
anzi si può senz’altro dire che tale ipotesi è l’unica possibile quando si
voglia escludere il cosiddetto «trascinamento
dell’etere».
Le formule relative sono date in dettaglio in appendice per i lettori che volessero approfondire la questione.
Nello sviluppare i calcoli relativi a questo nuovo modo di affrontare la questione abbiamo usato sistematicamente la notazione vettoriale allo scopo di scrivere sinteticamente le complicatissime formule del problema, lasciando al calcolatore il compito di fornirci le formule finali e così poter seguire più facilmente le operazioni concettuali.
Per eseguire i calcoli abbiamo usato il programma di calcolo simbolico «MAPLE»; dobbiamo tuttavia notare che, data la complessità delle formule, il tempo necessario per il risultato esatto sarebbe risultato eccessivamente lungo e, del resto, la formula finale sarebbe stata di tale complessità da risultare praticamente inservibile, quindi, da un certo punto in poi, ci siamo limitati ad eseguire i calcoli ricorrendo a sviluppi in serie in modo da ottenere risultati finali corretti fino al secondo ordine nelle variabili ρ (modulo della velocità orbitale della Terra, assunta come unitaria la velocità della luce nel vuoto) e μ (deviazione di uno degli specchi da introdurre per ottenere ragionevoli valori per l’intervallo tra le frange) come sarà meglio precisato in appendice, come peraltro hanno fatto tutti gli autori che precendentemente hanno affrontato il problema.
Il risultato finale è
spostamento relativo
= ![]() ,
,
dove ρ è il modulo della velocità dell’apparato nel sistema dell’etere, posta come unitaria la velocità della luce nel vuoto, lab è la distanza tra gli specchi a e b, λ è la lunghezza d’onda della luce monocromatica emessa dalla sorgente, μ è il piccolissimo angolo di cui bisogna disallineare lo specchio b, necessario per poter osservare le frange d’interferenza, δ è l’angolo tra la direzione della luce incidente e la velocità dell’apparato rispetto al sistema dell’etere, ε è l’eventuale differenza di lunghezza tra i due bracci dell’interferometro, introdotta da Righi per tenere conto di un eventuale errore sistematico nella misurazione di tali lunghezze.
Come si vede le formule finali risultano indipendenti dalla distanza, loa, tra la sorgente e il centro della lastra semiargentata a, come assunto da Righi e come derivato, in base al suo modello, da Valle.
Nelle formule finali di Valle è inclusa un’aberrazione all’entrata dovuta, secondo l’autore, alla circostanza seguente: supposto che la sorgente sia costituita da una sorgente puntiforme o lineare posta nel piano focale di una lente convergente, per cui durante il tempo in cui la luce viaggia dalla sorgente puntiforme (o lineare) alla lente, quest’ultima si è spostata solidalmente con l’apparato, ne segue che il raggio incidente subisce una deviazione pari a senα = ρsenδ.
È difficile per noi consentire con tale proposta dal momento che essa implicitamente presuppone che l’aggiustaggio empirico delle lenti venga effettuato in un sistema di riferimento fermo rispetto all’etere e non, come di fatto avviene, nel sistema dell’apparato.
Ad ogni modo abbiamo verificato che nel nostro modello l’introduzione di una tale aberrazione non ha alcun effetto sulle formule finali all’ordine di approssimazione in cui le abbiamo date.
Dal momento che nessun confronto è possibile con Villey, in quanto questi sembra accettare i risultati di Righi limitandosi a dare una diversa interpretazione ai risultati dello stesso, che in questo contesto non è di alcuna rilevanza, come già sottolineato da Valle, continuiamo con il confronto tra i nostri risultati con quelli di Righi e di Valle.
Al posto dell’ultima equazione Valle dà una formula, che con i nostri simboli e tenuto conto che egli considera solo il caso in cui sia ε = 0, è
spostamento relativo
= ![]() ,
,
cioè manca il termine in sin 2δ.
Righi si limita a dare la formula per lo spostamento relativo solo per δ = 0, che è
spostamento relativo
= ![]() .
.
Come si vede,
il nostro risultato per ε = 0 e δ = 0 coincide
con il risultato di Valle, è comunque diverso dal risultato di Righi che
permetterebbe, anche nel caso di ε = 0, un risultato nullo per
lo spostamento relativo, per
μ = -ρ/5.
Per quanto riguarda l’intervallo tra le frange il risultato per μ ¹ 0, trascurando tutti i termini di ordine superiore, è lo stesso del nostro per tutti gli autori. Per μ = 0, dove intervengono termini di ordine superiore si registrano, per i diversi autori, differenze che sono marginali, in quanto tutte le formule conducono alla previsione di un intervallo considerevolmente grande tale da rendere inosservabili le frange d’interferenza.
Le formule sopra derivate sono sufficienti a dimostrare, insieme al risultato sperimentale di Michelson e Morley, che non si può mantenere l’ipotesi di un etere stazionario rispetto al sistema solare quando si tiene conto solo della velocità orbitale della Terra.
Il tentativo d’individuare un moto cosmico più generale è stato preso in considerazione da Miller [11].
Miller osserva che fino al 1925 l’interferometro di Michelson è stato impiegato solo per verificare delle ipotesi specifiche e precisamente: l’ipotesi di un etere stazionario ma con l’assunzione di uno specifico moto della Terra rispetto all’etere e cioè veniva solo considerato il moto assiale della Terra insieme con il suo moto orbitale combinati con un supposto moto con velocità costante, pari a circa 19 km/s, di tutto il sistema solare verso la costellazione di Ercole. L’esperimento di Michelson e Morley del 1887 diede una risposta negativa a tale ipotesi. Successivamente gli esperimenti furono indirizzati a verificare l’ipotesi della contrazione dei corpi di Lorentz-FitzGerald, o a verificare supposte influenze sull’interferometro di effetti di magnetostrizione o di calore radiante o di deformazioni della struttura dell’interferometro dovuta alle forze gravitazionali.
Tali esperimenti condotti da Morley insieme con lo stesso Miller hanno dato, nel corso di diversi anni, risposte negative alle varie questioni poste.
Tuttavia in tutti gli esperimenti rimaneva un piccolo ma costante e sistematico effetto che non si era riusciti a spiegare.
A partire dal 1925, approfittando dell’alta sensibilità dell’interferometro, Miller decide di proseguire con gli esperimenti con lo scopo di accertare la presenza di un moto assoluto verso un punto (apex) da determinare indagando sistematicamente intorno a tale piccolo effetto residuo, ciò comportava di effettuare misure in modo sistematico in diverse ore del giorno e in diversi periodi dell’anno.
L’analisi dei dati, mediante le tecniche che utilizzano le trasformate di Fourier, degli esperimenti compiuti da Miller dall’aprile del 1925 al febbraio del 1926, lo portava a concludere che si poteva individuare un moto assoluto del sistema solare diretto verso un punto situato nella costellazione Dorado, Pesce Spada, a circa 20° a sud della stella Canopo, cioè la seconda più brillante stella del cielo. Più precisamente tale punto disterebbe solo 7° dal polo dell’eclittica e 6° dal polo del piano invariante del sistema solare.
Per quanto riguarda il valore assoluto della velocità del Sole, Miller trova il valore di 208 km/s, diretto praticamente, come si è detto, verso il Polo Sud e osserva che l’apparente moto del Sole in direzione opposta, rispetto alle stelle ad esso più vicine, di 19 km/s sta ad indicare che tale gruppo di stelle, vicine al Sole, si muove come un tutto con una velocità di 227 km/s.
Comunque restavano assolutamente non spiegate una riduzione di un fattore 20 per la velocità orbitale della Terra, quando è confrontata con i valori che si possono dedurre dai dati dell’interferometro e una variazione temporale dell’azimuth dell’apex.
Le analisi di
Miller sono comunque molto criticabili in quanto per la riduzione dei dati usa
la teoria elementare, dove non compare la dipendenza dello spostamento
dall’angolo δ tra la direzione del fascio incidente e la velocità assoluta
dell’interferometro e pone scarsa attenzione alla dipendenza del risultato
finale da μ e da ε, anche se nota che l’intervallo tra le frange dipende fortemente da
μ e il centraggio delle frange
dipende fortemente da ε.
Le analisi di Miller sono state criticate da Shankland et al. [12]. Ma le critiche di tali autori erano rivolte ad interpretare come effetti dovuti alle possibili variazioni di temperatura gli effetti sistematici sui quali era basata l’analisi di Miller. Ma, alla fine, pur rimanendo della loro opinione, sono stati costretti a concludere che non avevano dati sufficienti sulle temperature per confermare la loro ipotesi, riconoscendo l’indubbia sistematicità degli effetti trovati da Miller.
In conclusione possiamo dire che, anche se il problema del moto assoluto del sistema solare rispetto a un qualche punto dello spazio è ormai solo un argomento di storia della fisica, dal punto di vista sperimentale è, a nostro giudizio, ancora da risolvere se si dà credito ai risultati di Miller.
Appendice
Riferendoci alla fig. 1, indichiamo con a, b, c i tre riflettori, con a, b, c, rispettivamente, i tre versori che individuano le direzioni delle proiezioni dei riflettori sul piano della figura.
Dal momento che le nostre considerazioni sono limitate in un piano non è conveniente, per individuare la giacitura dei riflettori, usare, come più usuale, i versori normali ad essi; notiamo qui che utilizzando il calcolo geometrico di Peano è possibile scrivere semplicemente anche le formule relative al caso tridimensionale; qui ci limitiamo a considerare il problema bidimensionale come hanno fatto tutti i precedenti autori.
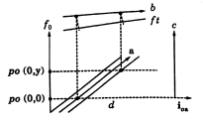
Fig. 1. — f0 indica la traccia,
nel piano del disegno, di un fronte d’onda piano che avanzando in direzione i0a
incontra prima la lastra semiargentata, a, che nel frattempo si muove
con una velocità arbitraria, v (non segnata in figura, tuttavia sono
segnate tre diverse posizioni del riflettore a, e cioè: a t = 0
e ai tempi d’incontro del riflettore con il raggio che si diparte da po (0,0) e con il raggio
che si diparte da po (0,y)),
quivi in parte si riflette verso lo specchio b e dopo un’ulteriore riflessione a un tempo t si trova in f
t continuando ad avanzare verso l’oculare d.
Sia d l’oculare, con il quale s’intende
osservare il fenomeno d’interferenza, supponendo che tale oculare venga focalizzato
in modo da osservare le frange d’interferenza sulla faccia dello specchio b.
Indichiamo con po (0,0) un punto del fronte d’onda, f0 che all’istante t = 0 si diparte dalla sorgente di onde piane; supporremo che po(0,0) sia allineato, all’istante t = 0, con i centri dei due riflettori, posti sulla linea del raggio incidente; indicheremo con po (0,y) un generico punto dello stesso fronte d’onda che si trovi alla distanza y dalla precedente linea dei centri dei riflettori.
In base alla nostra ipotesi, il raggio incidente, caratterizzato dal versore i0a che si diparte da po (0,y) all’istante t = 0, incontrerà il riflettore a nel punto pa(toa,y) all’istante toa(y), posto che il riflettore si muova con velocità v; in generale si ha
pa(t,y) =pa(0,y) + v
t.
Nel frattempo il raggio che si diparte da po(0,0) incontrerà il riflettore a in un punto più vicino alla sorgente (stiamo supponendo y > 0) e impiegherà conseguentemente un tempo minore.
Incontrando il
riflettore a, costituito da una lastra trasparente semiargentata, i due
predetti raggi verranno in parte trasmessi lungo i0a
e in parte riflessi lungo una direzione da determinare iab
.
Questi ultimi, riflettendosi a loro volta sul riflettore b, ricostituiranno il fronte d’onda lungo una retta f t da determinare, i cui punti siano punti di eguale cammino ottico, in accordo con il pricipio di Huygens.
Quindi questo
nuovo fronte d’onda risulterà inclinato di un certo angolo rispetto alla
direzione che avrebbe avuto se fosse stata nulla la velocità relativa tra il sistema dell’etere ed il sistema dell’apparato.
Lo stesso
avverrà per lo specchio c.
Per semplificare la scrittura dei vari passaggi algebrici conviene introdurre alcuni operatori che verranno ripetutamente usati nel séguito.
Indichiamo con N un operatore che ruota di 90°, in senso antiorario, un generico vettore nel piano del disegno.
Indichiamo con T(O, i, X0, s) quell’operatore che, dato il punto di partenza, O, di un raggio di luce lungo la direzione i ad un istante generico, fornisce il tempo impiegato dalla luce per incontrare un riflettore di direzione s, essendo X0 un punto di esso all’istante in cui il raggio si diparte da O, punto che si muove con velocità v nel sistema dell’etere, per cui durante il tempo necessario all’incontro si sarà portato in
(1) X = X0 + v Δt.
Per trovare l’espressione di tale operatore ragioniamo come segue, in riferimento alla fig. 2.
Sia P il detto punto d’incontro, se poniamo uguale ad uno la velocità della luce nel vuoto, si ha
(2) P - O = Δt i ,
(3) P - X = l s ,
per cui
(4) P = O + Δt i
= X+ l s ,
cioè
(5) X - O = Δt i - l s .
La (5), avendo posto js = N s, tenuto conto della (1) ci dà
(6) (X0 - O ) × js = Δt ( i - v ) × js
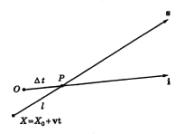
Fig. 2.
per cui
(7) ![]()
Conseguentemente sarà
(8) P = O + i T(O, i
, X0 , s).
Moltiplicando scalarmente per j = N i si ha anche
(9) ![]()
Ci sarà utile anche l’operatore
(10) ![]() ,
,
che si può semplicemente ottenere
dalla (7) ponendo v = 0; tale operatore ci dà la
distanza tra il punto O e il punto
d’incontro tra la retta di direzione i passante per O e la retta di direzione s passante per X0.
Il punto d’incontro tra le due rette sarà
(11) P = O
+ i I (O, i, X0 , s).
Introdurremo un ultimo operatore, R ( i, a), che fornisce la direzione del raggio riflesso date le direzioni del raggio incidente e del riflettore.
Siano ip , e in le
componenti parallela e normale (rispetto alla direzione, a, del riflettore) del
raggio incidente, i.
Si ha
(12) i = ip + in
(13) R ( i, a) = ip - in
per cui
(14) R ( i, a) = i - 2 in ,
che possiamo scrivere come
(15) R ( i, a) = i - 2 (i × ja ) ja
, ja
= N a .
I precedenti operatori sono sufficienti per scrivere in forma più compatta le formule generali del nostro problema.
Per prima cosa ci proponiamo di verificare che con tale interpretazione del principio di Huygens si ritrova più semplicemente la deviazione angolare dovuta al moto dei riflettori già trovata da Righi con una complessa costruzione geometrica [13] e poi ritrovata da Valle con non meno semplici procedimenti [14], anche se noi non avremo modo di usarla, dal momento che seguiremo il percorso dei singoli raggi nel sistema dell’etere con i riflettori in moto, tagliando corto così ad ogni discussione relativa al moto della luce per riflettori in moto sostituiti da quelli fermi opportunamente riorientati.
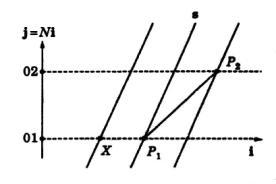
Fig. 3.
Facendo riferimento alla fig. 3, siano O1 ed O2 due punti del fronte d’onda incidente, distanziati da una lunghezza unitaria; porremo O2 = O1 + N i = O1 + j, essendo i la direzione del raggio incidente. Sia s l’orientazione dello specchio.
L’apparente orientazione dello specchio sarà data dal versore
(16) ![]() ,
,
con
(17) P2 - P1 = (O2 - O1) + i (T(O2 , i , X0 , s) - T(O1 , i , X0 , s)) ,
dove X0 è un punto generico dello specchio all’istante in cui si dipartono i raggi di luce del nostro fronte d’onda.
In base alla (7) si ha
(18) ![]()
Indicando, con Righi, con α l’angolo tra la direzione del raggio incidente ed una direzione arbitraria di riferimento, con β l’angolo tra la direzione della normale ad s e la stessa direzione arbitraria, con δ l’angolo della velocità rispetto alla direzione di riferimento, e con ρ il modulo della velocità, e, con Valle, indicando con Vn la componente della velocità dello specchio lungo la normale ad esso, con i, l’angolo d’incidenza, e con C, la velocità della luce, con qualche passaggio algebrico si trova
(19) ![]()
che sono le formule dell’aberrazione già trovate da Righi e da Valle.
Avendo dimostrato che il nostro metodo di applicazione del principio di Huygens è equivalente a quelli di Righi e di Valle, procediamo con il nostro metodo al calcolo dello spostamento, che non presenterà più alcun problema d’interpretazione per quanto concerne il moto della luce rispetto agli specchi fermi corretti per l’aberrazione dovuta al loro movimento.
In riferimento alla fig. 1:
Sia ioa la direzione del raggio incidente, cioè la direzione normale al fronte d’onda.
Siano, come sopra specificato, a, b, c, rispettivamente, i tre versori che individuano le direzioni delle proiezioni dei riflettori nel piano della figura.
Il raggio riflesso da a verso b è
(20) iab = R(ioa , a).
Il raggio riflesso da b verso d è
(21) ibd = R(iab , b).
Il raggio riflesso da c verso a è
(22) ica = R(ioa , c).
Il raggio riflesso da a verso d è
(23) iad = R(ica , - a).
Per quanto
detto sopra in relazione al principio di Huygens, tali riflessioni avvengono,
all’istante dell’impatto del singolo raggio, come se i riflettori fossero
fermi relativamente al sistema dell’etere.
Seguiamo quindi il percorso del raggio che si diparte dal punto po(0,y), che al variare di y descrive il fronte d’onda incidente, f0, al tempo t = 0.
Per un punto generico dell’apparato, come già detto, si ha
(24) p(t,y) = p(0,y) + t v
,
essendo v la velocità
dell’apparato nel sistema dell’etere.
Sia loa la distanza tra f0 ed il centro del riflettore a, che indichiamo con
(25) pa(0,0) = po (0,0) + loa ioa , all’istante t = 0.
Poniamo
(26) po(O,y)
= po(O,O) + y joa , con joa = N
ioa.
Il tempo necessario perché il raggio passante per p(0, y) incontri il riflettore a sarà
(27) toa = T( po(0,y) , ioa ,
pa(0,0) , a) ,
ed il punto d’incontro sarà
(28) pa(toa
, y) = po (0, y) + toa ioa .
Allo stesso modo e con evidente significato dei simboli si ha
(29) pb(0,0) = pa(0,0) + lab joa ,
essendo lab la lunghezza di uno dei bracci dell’interferometro;
(30) tab = T( pa(toa,y) , iab ,
pb(toa,0) , b) ,
(31) pb(toa
+ tab , y) = pa (toa, y) + tab iab .
Il raggio riflesso da b incontrerà di nuovo a dopo un tempo
(32) tba = T( pb(toa+ tab , y) ,
ibd , pa(toa+ tab, y) , a) ,
nel punto
(33) pa(toa
+ tab + tba , y) = pb (toa+ tab , y) + tba ibd .
Si può pensare che il raggio ibd provenga direttamente da una sorgente fittizia posta nel punto
(34) O1(0,y) = pa(toa
+ tab + tba , y) - (toa+ tab + tba ) ibd .
Allo stesso modo, per quanto riguarda il raggio che va verso c, si ha
(35) pc(0,0) = pa(0,0) + lac ioa ,
(36) toc = T( po(0,y) , ioa ,
pc(0,0) , c) ,
(37) pc(toc
, y) = po (0, y) + toc ioa .
Il raggio riflesso da c incontrerà di nuovo a dopo un tempo
(38) tca = T( pc(toc,y) , ioc ,
pa(toc,0) , - a) ,
(39) pa(toc
+ tca , y) = pc (toc, y) + tca ica .
Anche in questo caso si può pensare che il raggio iad , che si diparte dopo riflessione da a, provenga direttamente da una sorgente fittizia posta nel punto
(40) O2(0,y) = pa(toc
+ tca , y) - (toc+ tca ) iad .
Naturalmente, al variare di y, O1(0,y) ed O2(0,y) descrivono due fronti d’onda piani al tempo t = 0.
Ora il problema si riduce a trovare le frange di interferenza prodotte dai due fronti d’onda avanzanti verso un piano normale al piano del disegno di fig. 1 passante per la faccia dello specchio b (che, a sua volta, si muove con velocità v) dove, come si suppone, le frange verranno osservate da un osservatore solidale con l’apparato.
I due fronti d’onda avanzanti sono
(41) O1(t,y) = O1(0,y) +
t ibd ,
(42) O2(t,y) = O2(0,y) +
t iad .
L’intersezione, O(t), tra due singole rette, considerate all’istante t, appartenenti ai due fasci di rette (41) e (42), rappresenta la frangia centrale del sistema di frange, considerato all’istante t.
Al variare di t il punto O(t) descrive una retta, di direzione i, retta che possiamo considerare come un particolare raggio di luce, anche se la frangia centrale è scura in quanto i due fronti d’onda interferenti sono in opposizione di fase, stante che uno dei due raggi attraversa lo spessore della lastra semiargentata e l’altro no.
Tale fittizio raggio incontrerà il piano normale al piano del disegno passante per la retta che individua lo specchio b in un dato punto.
Per trovare tale punto notiamo, come già accennato, che O1(t,y) e O2(t,y) sono l’espressione parametrica, con parametro y, di due rette che rappresentano i fronti d’onda al tempo t, inoltre al variare di t si ottengono due fasci di rette parallele che rappresentano i due fronti d’onda luminosi avanzanti.
Data la relazione lineare rispetto a y e t, le direzioni dei due fronti d’onda sono indipendenti da t e sono date da
(43) 
(44) 
Usando la (11) possiamo trovare il nostro fittizio raggio di luce:
(45) O(t) = O1(t,0) + j1 I( O1(t,0) , j1 , O2(t,0) , j2).
La direzione
della traiettoria di O(t) è
(46) 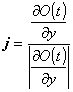 .
.
Ricorrendo alla
(9) troviamo la distanza del punto d’incontro di O(t) con lo specchio b dal
punto pb(0,0):
(47) ![]()
La frangia scura centrale si osserverà quindi ad una distanza d0° dal centro dello specchio b; ciò anche nel sistema dell’apparato, tenuto conto che le distanze relative restano immutate durante il movimento.
La frangia successiva si può ottenere ripetendo il procedimento a partire dalla (42), che viene sostituita dalla
(48) O2(y,t-λ) = O2(0,y) + (t-λ) iad ,
essendo λ la
lunghezza d’onda della luce incidente (ricordiamo che abbiamo scelto la
velocità della luce nel vuoto come unitaria), ottenendo il valore della
distanza della prima frangia scura (dopo quella centrale) dal centro dello
specchio e che indicheremo con dd0°
.
Ripetendo tutto intero il procedimento, questa volta con una velocità dell’apparato pari ad u = N v, si otterrà la distanza d90° della frangia centrale dal centro dello specchio b con l’apparato ruotato di 90° e la relativa distanza della prima frangia.
Lo spostamemto assoluto della frangia centrale per effetto di tale rotazione sarà
(49) spostamento assoluto = d0°
- d90° .
Lo spostamento relativo all’intervallo tra le frange sarà
(50) spostamento
relativo = ![]() .
.
Come già abbiamo accenato, i procedimenti simbolici sono stati affidati al programma di calcolo simbolico «MAPLE» e condotti in modo da ottenere nelle formule finali risultati corretti al secondo ordine nelle variabili ρ = | v/c | e μ = deviazione angolare dello specchio b, cioè ponendo b × ioa = cos μ . Più precisamente a partire dalle (41) e (42) si è proceduto a sviluppare le formule in serie di Taylor nelle variabili ρ e μ tenendoci anche i termini in ρ3, ρ2 μ, ρ μ2, μ3, in modo da avere risultati certi al secondo ordine. Nel caso che la formula non ammetteva uno sviluppo in serie di Taylor (espressione fratta nelle variabili ρ e μ) si sono sviluppati separatamente numeratore e denominatore.
La deviazione μ dello specchio b si rende necessaria, come già notato da Sutherland, Hicks, Righi e Valle, in quanto per μ = 0 l’intervallo tra frange successive verrebbe ad essere enormemente grande e le frange non risulterebbero visibili.
Il risultato finale fornitoci da «MAPLE» è:
spostamento assoluto = d0°
- d90° = ![]() ,
,
d0° e d90° sono le deviazioni subite dalla frangia centrale del fascio di luce diffratto nei due orientamenti dell’interferometro, rispetto alla posizione che essa avrebbe nel caso in cui l’interferometro fosse in quiete rispetto al sistema dell’etere, ρ è la velocità della Terra nel suo moto orbitale in unità di velocità della luce nel vuoto, μ è la supposta deviazione angolare a cui si deve assoggettare lo specchio b, λ è la lunghezza d’onda della luce incidente, lab è la distanza che separa il centro della lastra semiargentata a dal centro dello specchio b, ε = (lac - lab) / lab è l’eventuale differenza relativa nella lunghezza dei due bracci dell’inteferometro, introdotta da Righi, δ è l’angolo tra la direzione della velocità orbitale della Térra e la direzione della luce incidente sull’apparato.
Trascurando tutti i termini di ordine superiore si ottiene:
intervallo
tra le frange = dd0° - d0° =![]()
essendo dd0° lo spostamento subìto dalla frangia immediatamente vicina a quella centrale per effetto del moto relativo tra apparato e sistema dell’etere.
Tale intervallo risulta indipendente da δ, all’ordine di approssimazione considerato.
Per vedere cosa succede ponendo μ = 0 conviene dare una formula meno approssimata:
dd0° - d0° =![]() .
.
Dai precedenti risultati si ottiene la formula finale dello spostamento relativo da confrontare con i risultati di Righi e di Valle:
spostamento relativo = ![]() =
= ![]() .
.
Riferimenti bibliografici
[1] Per le considerazioni storico-epistemologiche rimandiamo a un nostro precedente articolo, vedi Di MAURO P., NOTARRIGO S. e PAGANO A., Il potere dei paradigmi: L’etere cosmico e la critica di Augusto Righi all’esperimento di Michelson-Morley, Mondotre/Quaderni, V, 9 ottobre 1993, p. 27, Siracusa; vedi anche Di MAURO P., Tesi di Laurea, Università di Catania, 1991.
[2] MICHELSON A. A., Am. J. Sci., 22
(1881) 120.
[3] MICHELSON A. A. and MORLEY E. W., Philos. Mag., 24 (1887) 449.
[4] SUTHERLAND W., Philos. Mag., 45
(1898) 23.
[5] HICKS W. M., Philos.
Mag., 3 (1902) 9.
[6] MORLEY E. W. and MILLER D. C., Philos. Mag., 9 (1905) 669.
[7] RIGHI A., Nuovo Cimento, XVI (1918) 213; XVIII (1919) 91; XIX (1920) 141; XXI (1921)
187.
[8] DALLA NOCE G., Nuovo Cimento, XXIV, 6 (1922) 17.
[9] VILLEY J., C. R. Acad. Sci., 17 maggio 1920, p. 1175, e 2 agosto 1920, p. 298.
[10] VALLE G., Nuovo Cimento, II (1925) 39, 171.
[11] MILLER D. C., Rev. Mod. Phys., 5 (1933) 203.
[12] SHANKLAND R. S., McCUSKEY S. W., LEONE F.C. and KUERTI G., Rev. Mod. Phys., 27 (1955) 167.
[13] RIGHI A., Nuovo Cimento, XVI (1918) 213.
[14] VALLE O., Nuovo Cimento, II (1925)171.