Pre-print
a cura degli autori. Originale pubblicato su:
Atti del
XVI Congresso Nazionale di Storia della Fisica e dell’Astronomia
a cura di
P. Tucci, pp. 355 – 360 CNR Gruppo di lavoro per le Celebrazioni Voltiane
Como,
maggio1997
Pietro Di Mauro, Salvatore Notarrigo
SULL’INVARIANZA DELLE EQUAZIONI DI MAXWELL
Einstein nelle lezioni di Princeton1 scrive:
“Per restare in accordo col principio di relatività nel suo significato
più lato, dovremo dare alle leggi una forma tale che valga in ogni sistema
quadridimensionale di coordinate; dobbiamo imporre cioè che le equazioni che
esprimono le leggi, siano covarianti per trasformazioni arbitrarie”.
E nella
memoria del 1916 scrive:2 “Le leggi generali della natura debbono
potersi esprimere mediante equazioni che valgono per tutti i sistemi di
coordinate, cioè che siano covarianti rispetto a qualunque sostituzione
(covarianti in modo generale).”
L’ambiguità di una tale formulazione è stata messa in evidenza da diversi autori3, in relazione a diverse questioni, fra l’altro, per il fatto ovvio che le equazioni di Maxwell si possono scrivere sia in forma covariante che non covariante, in dipendenza della arbitraria scelta del gauge, senza che per questo venga intaccata la loro validità fisica, nel confronto con l’esperienza.
Qui ci vogliamo soffermare su un’altra ambiguità che emerge dall’uso che Einstein, e con esso molti altri autori, fa della parola “covarianza”.
Non c’è dubbio
che la “covarianza”, rispetto a determinate trasformazioni di coordinate, è
condizione sufficiente perché le equazioni che esprimono le leggi fisiche
restino invariate in forma.
Ma non c’è nemmeno dubbio che la “covarianza” non basta per assicurarci che una grandezza fisica resti invariata in “valore” per effetto della trasformazione.
Sembra che per Einstein la covarianza implichi entrambe le cose.
Per capire da dove proviene tale ambiguità conviene esaminare storicamente la nascita e i successivi usi della cosiddetta trasformazione di Lorentz.
In un libro edito nel 1924, Burali-Forti e Boggio4 sviluppano alcune ricerche su questo argomento, facendo seguito a un precedente lavoro di Somigliana5. Riteniamo utile riassumere, per il seguito, tali risultati, aggiungendovi alcune ovvie conseguenze.
È noto che, introducendo l’operatore dalembertiano:
![]()
assumendo il gauge di Lorentz e ponendo c=1, le equazioni di Maxwell si possono scrivere sotto la forma:
1) [ ]2 A = - J
dove A = {Ax , Ay , Az , i At } e J = {Jx , Jy , Jz , iJt} sono quadrivettori complessi.
Nel caso particolare in cui J = 0, indicando con f(r,t) una generica componente del quadrivettore A essa obbedirà all’equazione dell’onda:
2) ![]()
la cui soluzione generale è della forma:
3) ![]()
con F e G funzioni arbitrarie dei loro argomenti.
Si verifica subito che, se introduciamo la trasformazione:
4) 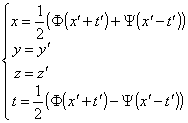
con Φ e Ψ funzioni arbitrarie dei loro argomenti, la (1) resta invariata in forma, se si ridefinisce opportunamente il quadrivettore J′. Infatti basta porre:
5) ![]()
Quindi le trasformazioni della forma (4) lasciano invanate in forma le equazioni di Maxwell, dal momento che J′ è ancora un quadrivettore. Anzi tali trasformazioni formano un gruppo poiché il prodotto di due di esse origina un’altra trasformazione della stessa forma.
Nel caso particolare di trasformazioni lineari, cioè con
6) ![]()
con a e b costanti, si ha:
7) 
e la (5) diventa:
8) J′ = abJ .
Se invece si pretende l’invarianza in valore, cioè
J′2 = J2 ,
allora bisogna porre:
![]()
condizione che non è facile soddisfare in generale, ma che nel caso lineare si può soddisfare, ponendo
![]()
Notiamo che
se, in questo caso, poniamo
![]() ,
,
si ottiene la trasformazione di Lorentz.
Quindi la trasformazione di Lorentz non è l’unica che lascia invariate in forma le equazioni di Maxwell, essendovene financo di non lineari.
Lo stesso Lorentz6 espone le sue formule moltiplicando le quattro equazioni della trasformazione oggi detta di Lorentz per un’arbitraria funzione, l , della velocità relativa dei due sistemi e nella nota alla pagina successiva ricorda che tale trasformazione era già stata trovata dal Voigt.
Solo successivamente, in base al suo particolare modello di elettrone, pensa che bisogna porre l = 1 per mettere d’accordo il rapporto tra massa trasversale e massa longitudinale con il risultato nullo dell’esperimento di Michelson.
Per Einstein, invece, la trasformazione di Lorentz è l’unica che lascia invariate le equazioni di Maxwell per la ragione, come si può facilmemente supporre, che nella memoria7 del 1905 pone arbitrariamente a(v) = a(-v) (indica con a, la l che compare nelle formule di Lorentz ) con argomenti fallaci basati sulla simmetria di un ipotetico esperimento fatto con fotografie istantanee (la fallacia dell’argomento sta nel considerare solo il caso in cui x′=0, dove l’inversione del verso della velocità del moto relativo non altera la condizione di allontanamento o di avvicinamento dei due osservatori; la cosa non è più così per x′¹0 come si verifica sperimentalmente anche nell’effetto Doppler).
Nelle lezioni di Princeton stranamente crede di derivare le trasformazionidi Lorentz dall’ipotesi
Δ x12 + Δ x22 + Δ x32 - c2 Δ t2 = 0
dicendo: “questa condizione è sempre soddisfatta se è soddisfatta la condizione
più generale [sic!; di fatto, come
ognuno può vedere, è più restrittiva!] che, per la trasformazione di Lorentz, sia invariante s2 = Δ x12
+ Δ x22 + Δ x32
-
c2 Δ t2 ” .
Noi pensiamo che sia questa la causa del mito corrente secondo il quale la trasformazione di Lorentz sia l’ unica che lascia invariate in forma le equazioni di Maxwell.
La trasformazione di Lorentz lascia di fatto invariato, anche in valore, il modulo della quadricorrente, | J | , anche se dal punto di vista puramente matematico ve ne sono delle altre; p.es., alla prima e alla quarta equazione delle (4) si può sostituire:
![]() ,
,
ma è difficile interpretare tale trasformazione come riferentesi a due sistemi in moto relativo uniforme tra loro, a meno di non porre
![]()
che però riconduce alla usuale trasformazione di Lorentz.
Per concludere, esistono infinite trasformazioni, anche non lineari, che lasciano invariate in forma le equazioni di Maxwell. Matematicamente ne esistono anche altre che lasciano invariato anche in modulo il quadrivettore corrente, ma se si pretende che la trasformazione si riferisca a due osservatori in moto relativo uniforme tra loro, allora la trasformazione di Lorentz risulta l’unica che compia tale miracolo, cioè: J′2 = J2, ammesso che si riesca a dare un significato fisico a quest’ultima invarianza, dal momento che per calcolare il modulo di J bisogna sommare assieme il quadrato di una densità di carica con il quadrato di una densità di corrente, che pur essendo quantità equidimensionate (avendo introdotto l’opportuna potenza della velocità della luce), non sono grandezze della stessa specie e quindi non sommabili tra loro. Infatti si sommano le grandezze e non i numeri e la somma tra grandezze può solo essere definita operativamente, avendo prima escogitato un operazione fisica capace di confrontarle, senza di questo nessuna teoria fisica potrebbe essere verificata sperimentalmente!
NOTE
1 A.
Einstein, Il significato della relatività,
Einaudi, 1955, p. 69 TORNA
2 A. Einstein, Die Grundlage der allgemeinen Relativitastheorie, Annalen der Physik, (4), 49, 1916. Tradotta in italiano in Cinquant’anni di relatività, (a cura di Pantaleo), Universitaria Editrice, Firenze, 1955, p. 514. TORNA
3 Vedi anche Hong-Yee Chiu, W. F. Hoffmann, Gravitation and Relativity, Benjamin, 1964. TORNA
4 Rurali-Forti, T. Boggio, Espaces Courbes --- Critique de la Reiativité, Sten Editrice, Torino, 1924. TORNA
5 M. C.
Somigliana, Sulla trasformazione di Lorentz, Rend. R. Accad. Lincei,
Serie 5a, Vol. XXXI,
1° sem. 1924. TORNA
6 H. A. Lorentz, The Theory of Electrons, Teubner, 1909, p. 197. TORNA
7A. Einstein, Zur Elektrodynamik bewegter Körper, Annalen der Physik, 17,1905, p. 891, Tradotta in italiano in Cinquant’anni di relatività, (a cura di Pantaleo), Universitaria Editrice, Firenze, 1955, p. 514. TORNA