Pre-print a cura dell’autore. Originale pubblicato su:

IL NUOVO CIMENTO     VOL. 83B, N. 2    11 Ottobre 1984

 

 

A Newtonian Separable Model which Violates Bell’s Inequality (*)

 

S. NOTARRIGO

 

Istituto Dipartimentale di Fisica dell’Università - Catania

Gruppo Nazionale di Struttura della Materia - Catania

Istituto Nazionale di Fisica Nucleare - Sezione di Catania

 

 

(ricevuto il 16 Novembre 1983; manoscritto revisionato ricevuto il 20 Agosto 1984).

 

 

 

 

 

Summary. — On the basis of the Mackey’s axiomatization of quantum mechanics an argument is given which allows, in determinate circum­stances, the violation of Bell’s inequality also in a «classical mechanics» and a «classical probability» context. A mechanical model made out of two separate subsystems of coupled oscillators is studied by computer ex­periments to illustrate the point. In fact, the model violates Bell’s inequality. The hypothesis is put forward that the principal reason for this violation is due to the special kind of « detectors» introduced in the model which give a «count» every time a given dynamical variable of the mechanical system crosses an assigned threshold.

 

PACS. 03.65. — Quantum theory; quantum mechanics.

 

 

 

1. — Introduction.

 

In two well-known papers, BELL (1,2) succeeded in demonstrating that previous impossibility proofs of «hidden variables» in quantum mechanics were wanting because of too restrictive assumptions on their mathematical structure (1). However, he proposed (2) an inequality which must be satisfied by any hidden-variable theory, under certain separability requirements, in order to restore causality in a gedanken experiment of EPR type (3) in the Bohm-Aharonov (4) version.

The inequality is violated by quantum mechanics in certain instances.

Those papers have stimulated many researches both theoretical and ex­perimental, as can be seen in the reviews contained in ref. (5-8).

Most experiments favour quantum mechanics and hence seem to refute local physical theories which would continue to mantain the existence of «elements of reality» as defined in ref. (3), unless we are willing to introduce certain nonlocal featuires which, however, would «resolve the EPR paradox in the way which EINSTEIN would have liked least», to quote BELL (1). Many physicists believe that the conclusions to be drawn from the present experimental results «are philosophically startling: either one must totally abandon the realistic philosophy of most working scientists, or dramatically revise our concept of space-time», as, e.g., we read in the abstract of ref. (7).

A way-out of this dilemma may be to question the significance of Bell’s inequality.

This way has already been pursued by many authors on different grounds.

One is the argument, maintained in ref. (9,10), that the hypothesis of Bell which assigns a unique probability distribution to the hidden parameters in the different observational directions is too restrictive for not considering that the measurement process will affect in some way the probability distribution by changing the state of the system.

In the present paper I shall analyse the above argument on a different basis.

The conclusion will be that the argument is correct because of different reasons than those connected with the change of state introduced by the measurement process.

We shall see that the reason resides in the interpretation that one presup­poses, for the probabilistic concepts as applied to quantum and classical physics.

This point is illustrated in a more general context by FINE (11).

 

 

2. — Paradigmatic inequality in EPR physical situations.

 

It is often believed that «quantum mechanics purports to be a description of physical reality which deliberately eliminates from theory all features not demanded by experiment»(12).

However, it is not so easy te pursue this aim and other people think it is not worth and even misleading; but, in this limited context, in order to clarify the issue without unnecessary metaphysical presumptions, I shall try te de­scribe the physical situation avoiding any term which cannot be reconducted to experimental observations or manipulations.

In such terms, the paradigm in which Bell’s inequality is derived is the following: there is a «physical system» S defined by certain physical manipu­lations. On both sides of S, in a given spatia1 direction which we call the z-axis, we have a pair ef objects P1 and P2 which we call «polarizers», each characterized by a unit vector θ1 (θ2) in the plane normal to the z-axis.

The directions of these vectors can be varied by opportune knobs.

We have, in series to the «polarizers», two «detectors» D1 and D2 which register «counts» in the presence of S .

We have also a «coincidence system» which gives a «count» if and only if, separately, two «counts» will be registered in D1 and D2 within a fixed interval of time which we call the «resolving time».

The «polarizers» affect the counting intensity of the two «detectors» n(θ1) and n(θ2) and, hence, of the «coincidence», n(θ1 , θ2) in dependence of the setting of the knobs. Now we abandon the realm of «observations» and hypothesize a set Λ of variables λ associated with a probability density ρ(λ) defined as the Radon-Nikodim derivative of a probability distribution over the Borel subsets of Λ with respect to the Lebesgue measure (13).

Each value of λ determines univocally the registering or not of a count in either of the two detectors (and hence also in the coincidence system) at a given instant of time. This for any given set of directions of the polarizers.

The separability (locality) requirement is expressed (2,14) by pretending that the registering of a count on one side is not influenced by the setting of the knob on the other side.

Moreover, we assume that, whenever the two polarizers are set in the same spatial direction, we have with certainty a count in the coincidence system every time we have a count in one of the two detectors. Under this hypothesis we are able te know, for a given direction, what will happen on one side if we know what ought to happen on the other side in the chosen common direction, so that we may limit ourselves to consider the possible outcomes, determined by the values of the λ’s, on one side ouly.

Thus, if we choose three arbitrary possible directions θ1 , θ2, θ3 , for a polarizer they will partition the Λ-space in eight disjoint subsets of measure P({Aθ1 , Aθ2 , Aθ3}) with Aθi a variable which assumes the values unity or zero according to the registering or not of a count in the direction  θi  at a given instant of time.

We suppose that the counting intensities are proportional to the corre­sponding probabilities, this hypothesis is necessary to connect theory to possible experiments (5,7), thus we write (following an analogous reasoning in ref. (5,14))

 

(1)       

 

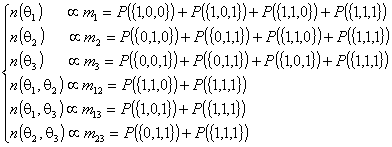
let us define

 

 (2)      

 

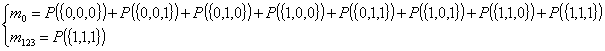
By solving the linear system with respect to P({Aθ1 , Aθ2 , Aθ3}) , we get

 

(3)       

 

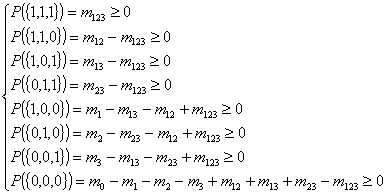
By summation

 

(4)                               

 

by dividing by m3 ³ 0,

 

(5)                                           

 

or, in terms of the counting intensities,

 

(6)                                           

 

This last inequality is violated when we identify the system S with a pair of photons in a J = 0 ® 1 ® 0 atomic cascade, analysed by two ideal polarizers P1 and P2 and detected by two photomultipliers D1 and D2; in this case we have (7)

 

 (6)                                           ;

 

if we choose θ1= 0°, θ2= 60°, θ3= 30°,

 

we get

 

(8)                                  cos2 30° + cos2 30° £ 1+ cos2 60°,

 

i.e.

 

(9)                                                            which is false.

 

There is nothing te object to this line of reasoning. But there is something to object to the supposed generality of the assumptions made for the significance entailed by the probabilistic structure of the hydden variables. This struc­ture cannot encompass even quite simple physical situations in a «classical mechanics» and «classical probability» context.

I shall give an example of such a situation in the next section, by now I want to analyse the issue from the theoretical viewpoint by resorting to a well­known axiomatization of a general physical statistical theory (15) (see also ref. (11)). In this axiomatization (11,15), the probability measure is defined as a function p which assigns a real number 0 £ p(A , α , E) £ 1 to each triple A , α , E, where A is an observable, α is a physicad state and E is a Borel subset of the real line R.

We have      p(A , α , φ) = 0   (φ represents the empty set),       p(A, α, R) = 1,

          p(A, α, E1 UE2 U ...)   =    p(A, α, Ej)  for Ej disjoint in pairs.

This first axiom is enough, for the moment, to draw some conclusions.

We note, first, that this probability measure defined on the Borel subsets of the real line is Kolmogorovian and hence is «a perfectly ordinary variety of statistical theory» (11).

As a second point we note that the observable A and the state α are to be thought as parameters (or sets of parameters) which fix the probability measure, so that, if the state and/or the observable change, then they will induce a change also on the Borel measure p.

Until now we are dealing with an abstract setting. Of course a good ax­iomatization is very useful to clarify the formal relations among the objects of our discourse but is not a substitute for the elucidation of the meaning of concepts. This can be accomplished by the interpretation of the abstract formalism in concrete physical situations.

In classical statistical mechanics, the observable A will correspond to a Borel function, on the phase space of the given dynamical system, which takes values on the real line R. The state α will be identified with a unique Borel measure on the family of the Borel subsets of the phase space of the system and is determined by the macroscopic constraints. This Borel measure will, univocally, determine the function p on the Borel subsets, E, of the range of the possible values of the dynamical variable A, namely p(A, α, E) = α (A-1(E)) (15).

In quantum mechanics the observable A will correspond to a self‑adjoint operator in the Hilbert space of the quantum system. The state α will be re­presented by a unique density operator in that space. The probability will be p(A, α, E) = tr [α A(E)] , with A(E) the spectral measure of the Borel set E (15).

The previous examples are already given in ref. (11,15), we recall them f or easy reference in the following discussion and, to this end, we give one more example which will be, too, useful later and take it from the theory of random noise (16).

Consider a function of the time f(t). Under certain circumstances it can be thought as the time hystory of a stochastic process (f(t) may be the voltage at each instant of time at the output of a photomultiplier). The observation of such a function over a finite time interval is called a «sample record» of a stochastic process f(t - τ) with τ a random variable. Sometimes an investigation of zero crossings or arbitrary level crossings of such sample records (16) is re­quired.

The statistical setting set forth before allows us an interpretation also in this case. Here the state α may be represented by the function f(t). The observable A may be the number of level crossings in a fixed time interval, starting from the random instant of time τ. In this case the probability measure will be concentrated over the integers.

We must stress here that, in all previous examples, according to the original definition, the probability measures are always defined on the Borel subsets of the real line (and hence perfectly «classical»), but such Borel measures are determined jointly by the state α and by the observable A. Thus it is not legitimate, in general, to use the same Borel measure as a probability measure for different observables.

This point will be relevant for an assessment of the significance of Bell’s inequality which is just derived from the hypothesis of the existence of such a unique Borel measure over the space Λ.

All this will be illustrated by a classical (Newtonian) system which will fill in the «black box» of our paradigmatic EPR physical situation.

Our system S will be «separable» and described in a «classical» prob­abilistic structure, partaking of all the three examples just mentioned. However, it violates the inequality derived before.

 

 

3. — Systems of linear, transversal oscillators.

 

Now we suppose that our system S is constituted by two identical sub-systems S1 and S2 each made of a one-dimensional lattice of n + 2 classical particles with linear interactions between nearest  neighbours only.

The equilibrium positions of all the particles in both subsystems are aligned along the z‑axis, but the particles are free to oscillate in the (x, y)-plane.

We suppose that, in both subsystems,

 

a)        the elastic constants in the longitudinal direction are stiff enough so that we have, practically, only transverse vibrations;

 

b)        the transverse couplings and masses are identical for all particles;

 

o)        the particles with index ρ = 0 and ρ = n + 1 are constrained to their equilibrium positions.

 

Under such assumptions, for each subsystem, the equations of motion for two orthogonal directions, normal to the z-axis, are (by choosing a natural time unit T = 1/ω)

 

(10)                 

 

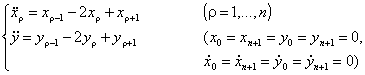
The eigenfrequencies are given by (17)

 

(11)                             

 

We give identical initial conditions to both subsystems:

 

(12)                 

 

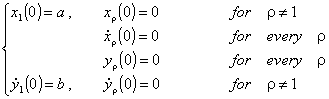
The solutions may be easily found:

 

the vibration state in the (x, y)-plane may be represented by the complex vector

 

(13)                        

 

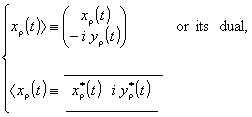
with

 

(14)                             

 

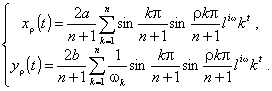
If we introduce the unit vector

 

(15)                                                      ,

 

the vibration amplitude along any given direction  of the (x, y)-plane for particle ρ will be given by the real part of the scalar product between the state  and the polarization state  corresponding to the projector   ,     i.e.

 

(16)                                                      Re .

 

Now we specify the kind of «polarizers» we want to introduce in our «black box». These will be constituted, in each subsystem, by constraints ori the par­ticles with ρ = σ (1 < σ < n) which impede vibrations along a specified direc­tion in the (x, y)-plane by letting the particle vibrate only along the orthogonal direction, say , which we call the «easy direction», this implies the equation of the constraints:   xσ  sin = yσ cos    on each side.

It is obvious that, if we give initial conditions different from zero only at particles with ρ < σ , the vibration state of all particles will change with re­spect to the state without constraints but of same initial conditions; however, the vibration component along the «easy direction» will not be affected by the constraints.

Moreover, for ρ ³ σ it will be the only component actually present and, for such particles, we have a state of linear polarization along the «easy direction» , so that our constraint may be represented by the projecter .

It remains to us to specify the «detectors»: we assume that the detectors are such that, without perturbing in any sensible way the system, they give a «count» every time some appropriate dynamical variable crosses a given threshold with positive slope. As particular instance of such dynamical va­riables, we have chosen the vibration amplitude or its square modulus, along the «easy direction» of two specified particles, one for each side, namely the particles with ρ = n.

This system simulates the paradigmatic EPR situation.

There are many ways te randomize our system: we may choose to treat as random variables the initial constants a and b in formulae (12) and (14), in this case we have the standard situation in classical statistical mechanics if, for instance, we look for the probability distribution of a given dynamical variable, as the vibrating amplitude of a particle in a given direction (formula, (16)) and so on.

However, if we are interested in the number of level crossings or the number of coincidences in a given time interval, the situation is more like to the random‑­noise example. The probability measure, in this case, is not so easily related to the probability measure, over the phase space, which defines the statistical state of the system but is altogether well defined.

There are, of course, other ways to randomize the system: by randomizing any of the constants which define the system as the number of particles, the elastic constants and so on; the simplest way, actually chosen in our model, is to fix the initial conditions and randomize the instant of time in which we enter into the process by counting the number of levol crossings and the number of coincidences in a fixed interval of time.

Unfortunately it is not easy to write down a usable algebraic expression which gives in a closed form the number of level crossings as a function of the fixed parameters of the systems but we may resort to the computer. Thus it has been done by means of a program which finds out the zeros of a generic function. In our case the problem was that of finding the number of level crossings for two of the functions defined by formula (16), or its square moduli, one for each subsystem, and the number of coincidences within a fixed resolving time relative to same pair of polarization directions  and .

In different computer experiments we varied the number n of particles, the initial constants a and b of formula (14), the resolving time of the coincidence, the «detection threshold», the duration of the counting time interval and the epoch τ of entering into the process.

We observed that the vibrating amplitude (16) behaved in an apparently very random way after a short time of about a factor two the interval for the first reflection of the initial wave pulse which was of about n natural time units. Also the interarrival times of threshold crossings appeared perfectly random. Their statistical distribution was stationary in the explored time range (@106 natural time units) and almost independent of the number of particles n.

The mean value of such interarrival times was of about three natural time units and the standard error of about one time unit.

Choosing, as crossing quantity, the square modulus of the vibrating am­plitude with initial constants (12) a = 1, b =  (these initial conditions would impress a uniform circular motion to the particle with ρ = 1 in case we should constrain at rest the particle with ρ = 2 with a threshold for both detectors of 0.001 and a resolving time of the coincidence of 0.63), we obtained, for the ratio defined in formula (7), a function quite near to the  law.

Actually it was almost identical for = 30° and n > 20; it deviated some­what in the other directions (the system is not rotationally invairiant) or for smaller number of particles.

However, by defining the ratio

 

(17)                                                     

 

as a measure for the degree of violation of inequality (6), we found that this ratio was under the limit fixed by inequality (6) for a very small number of particles, but increased steadily remaining at the value of the cos2 law from n = 20 to n = 100 which was the maximum number explored.

When we took the vibrating amplitude, instead of its square modulus, the violation was ever greater but the ratio (7) was not any longer similar to the cos2 law. We have already noted that our system, for the particular initial con­ditions, is not rotationally invariant; however, the number of «counts» as a function of the direction, i.e. , varied of less than 10% with a minimum value at 90°. It was instead quite constant by choosing initial constants a = 0.345 and b = 0.345, but in this case the ratio (7) was not so near to the cos2 law, nevertheless it violated all the same inequality (6) by the same amount of the cos2 law by choosing other three directions, namely = 45°, = 105°,= 75°.

Let us pause al this point and note that in our model we have a situation similar to our random-noise paradigm. However, given the peculiarity of our system we have many points in common also with the paradigm of quantum mechanics. In fact, for each particle of each subsystem we have a state space of vectors  which is isomorphic to the state space of the vectors which re­presents the polarization states of a photon in quantum mechanics; moreover, we have linear operators as the projector ; we, analogously, may construct a product space for the two subsystems and so on.

In our case, too, the probability measure for a given physical quantity is determined jointly by the state  and the operator  as far as the simple subsystem is concerned or by the product state and product operator for the composite system.

It may not be the case that such a probability measure will be determined by the same rules as in quantum mechanics but, in other respects, the system is perfectly analogous.

However, in our Newtonian separable (actually «separate») model we have found initial conditions, values of detector threshold and of coincidence re­solving time which simulate a quantum system also in probability measure.

Notwithstanding we must stress here that we are not proposing in any way a model for any quantum system but only give an instance in which Bell’s inequality is violated in order to illustrate, with a concrete example, the theo­retical point we made before.

As a last point we shall consider the empirical implications of our fìndings. Let us remind that in our Newtonian system the projection of the amplitude given by formula (16) is not modified by the «polarizer», so it is a property of the system independent of any particular observation made through a pair «polarizer-detector». (In fact, we can do away altoghether with the «polarizers» by easily devicing opportune «detectors» which do not perturb in any way the physical state of the system.)

Thus it has a meaning also in the particular case with a single vibrating oscillator for each side (18).

In this simple case one can, more perspicuously, see the reason why Bell’s inequality is violated; in fact, in this case the square modulus of the amplitude at an angle  will be

 

 

If Th is the value of the detector threshold, the crossing times will be

 

 

with c(Th) not depending on  and r an integral number.

For three directions  ,  and  and for a given r

 

 .

 

By choosing a resolving time for the coincidence circuit

 

         or       

 

inequality (6) will be trivially satisfied.

In fact, in the first case, all correlated events in the three channels will stay inside the resolving time, while, in the second case, only one for each channel will be inside the resolving time. In this case the ratio corresponding to that given by formula (17) is unitary. But, if we take,

 

 ,

 

the corresponding ratio will be r = 2, grossly violating inequality (6), because we have a coincidence in channel pairs  and , but not in channel pair , in spite of the fact that the three events in the different channels are totally correlated.

By opportunely weighting these two extreme cases, as, in practice, it was achieved by our model, we can obtain also the QM value, .

The finite resolving time of the coincidence eliminates the correlations be­tween certain pairs of channels and, vice versa, by the same mechanism, it may introduce spurious correlations between uncorrelated channels (19).

Because these effects are not connected with nonlocality, in fact, an ideal experiment can be easily deviced which conforms to all requisites of the more detailed «black box» proposed recently by BELL (20); in any experiment in­tended to test quantum mechanics in connection with the EPR paradox (3), one must, beforehand, check the invariance of the statistical distribution of the coincidence time intervals against the variation of the relative angle of the polarizers also in the case in which particular devices aro being used to test nonlocality as, for instance, in the experiment reported in ref. (21).

 

 

4. — Conclusions.

 

The theoretical considerations made in sect. 2 supported by the concrete example of sect. 3 convince us that Bell’s inequality is not so general as com­monly believed. Thus it cannot represent an impediment to a completion of quantum mechanics according to the original ideas of EPR (3).

The advantages of a «realistic» interpretation of quantum mechanics, also from a heuristic point of view, has been often stressed by eminent physicists and philosophers (see, in particular, ref. (22,26) ).

It is opportune at this point to try an assessment of the limits of validity of Bell’s inequality.

To do so, it is useful to consider some more elements of Mackey’s axio­matics (15): let us call an observable Q a «question», if in every state α the measure p(Q, α, E) is concentrated in the points 0 and 1, that is p(Q, α, {0, 1}) = 1. The functions mα(Q) = p(Q, α, {1}) define a natural partial ordering over the set of questions if we pretend that Q1 £ Q2 if and only if mα(Q1) £ mα(Q2) for all states α.

A question may always be constructed from an observable A, given a Borel subset E, by taking the question φE(A) with φE(x) the indicator of the set E,  i.e.  φE(x) = 1  for  x Î E and φE(x) = 0  for x Ï E. We shall indicate with such a question.

In classical statistical mechanics a question is simply a Borel function that takes on only the values 0 and 1; it is uniquely determined by the Borel subset of the phase space on which it takes the value 1; the function mα mapping questions into numbers becomes the measure which defines the state on the phase space.

For a given state α the Borel measure is unique, according to the definition  (ref. (15)) and we may think of classical phase space as the Boolean algebra of all its Borel subsets; in this case, obviously, Bell’s inequality is generally valid.

This may not be so if we consider, as a physical observable quantity, the number of level crossings of a classical dynamical variable. In this case, by fixing the numerical value of the threshold, we shall have different Borel measures for different dynamical variables because, by equating these variables to a constant value, different hypersurfaces are determined and our elementary events are just given by the points in which the dynamical trajectory of the system crosses such hypersurfaces.

In this case the lattice of the questions may not be any longer Boolean (27) (we remind that the partial ordering in the present axiomatization is deter­mined by the probability measure (15)).

It is interesting at this point to remind that it has been demonstrated (28) that with the usual axioms a lattice must necessarily be Boolean if a Kolmo­gorovian probability measure is supposed as a unique function on the elements of the lattice.

This allows us to understand why in our system of oscillators we have non­commuting operators, like the projectors , and, however, we can make simultaneous physical measurements of any corresponding quantities. It can be said that, in our model, two observables are incompatible when they cannot be described statistically by a unique Kolmogorovian probability measure over a Boolean algebra of the Borel subsets of some opportune phase space, without reference to the physical possibility of performing a measurement.

We can ask ourselves if the preceding notation could be an hint in order to give a meaning to the concept of incompatible observables in a future «real­istic and causal» interpretation of quantum mechanics.

By now we must have this question open, but only remind that a purely statistical interpretation has already been advocated (29).

We, however, remind that in our model we have a two‑dimensional linear vector space (the space of the polarization states), we have associated experi­mental questions to the system through opportune «polarizers» and «detec­tors». However, the lattice of those question is not Boolean, because the cor­responding projectors of the linear vector space do not commute, but simply modular (27). We have defined joint probabilities , but we do not have a subtending phase space of variables λ with a unique Borel measure over it (moreover, our system is not metrically transitive (30), i.e. in our model it is possible to decompose the phase space into invariant parts of positive measure (30)); but we have «many» Kolmogorovian measures, one for each «ob­servational state» different from the «physical state» of the system.

Here we stress the fact that neither the «polarizers» nor the «detecters» need, «physically», affect the «physical state»  of the system.

Of course, a «generalized probability measure» (31) could be defined over the lattice of the experimental questions and, in other contexts, it may result very usefull and important; however, in our limited context it does not help in clarifying our particular issue, where, by quoting one of the referee, prob­ability spaces are more important than more probability measures.

 

* * *

 

Thanks are due to Profs. J. S. BELL, G. FONTE, D. GUTKOWSKI, G. LOCHAK, M. SACHS and Dr. G. C. SCALERA for useful comments on a preliminary draft of the present paper; thanks are due also to one of the referees for useful sug­gestions.

 

 

 

 

• RIASSUNTO

 

L’assiomatizzione della meccanica quantistica di Mackey permette, in determinate circostanze, la violazione della disuguaglianza di Bell anche in un contesto di «meccanica classica» e «probabilità classica». Si studia al calcolatore un modello meccanico costituito da due sottosistemi separati di oscillatori accoppiati che violano la diseguaglianza di Bell e si fa l’ipotesi che la principale ragione di tale violazione è da imputare ai particolari «rivelatori» introdotti nel modello che forniscono un «conteggio» ogni qual volta una determinata variabile dinamica del sistema superi una soglia assegnata.

 

 

 

NOTE AND REFERENCES

 

(*)        To speed up publication, the author of this paper has agreed to not receive the proofs for correction.   TORNA

(1)  J. S. BELL: Rev. Mod. Phys., 38, 447 (1966).

(2)  J. S. BELL: Physics, 1, 195 (1964).

(3)  A. EINSTEIN, N. ROSEN and B. PODOLSKY: Phys. Rev., 47, 777 (1935).

(4)  D. BOHM arid Y. AHARONOV: Phys. Rev., 108, 1070 (1957).

(5)  E. J. BELINFANTE: A Survey of Hidden-Variables Theories (Oxford, 1973).

(6)  B. D’ESPAGNAT: Conceptual Foundations of quantum Mechanics (Reading, Mass., 1976).

(7)  J. F. CLAUSER and A. SHIMONY: Rep. Prog. Phys., 41, 1881 (1978).

(8)  F. M. PIPKIN: Adv. At. Mol. Phys., 14, 281 (1978).

(9)  L. DE LA PENA, A. M. CETTO and T. A. BRODY: Lett. Nuovo Cimento, 5, 177 (1972).

(10) G. LOHAK: Found. Phys., 6, 173 (1978).

(11) A. FINE: in Problems in the Foundation of Physics, edited by M. Bunge (Berlin, 1971), p. 79.

(12) F. A. KAEMPFFER: Concepts in Quantum Mechanics (New York, N.Y., 1965), p. 1.

(13) W. FELLER: Introduction to Probability Theory, Vol. 2 (New York, N.Y., 1966), p. 136.

(14) E. P. WIGNER: Am. J. Phys., 38, 1005 (1970).

(15) G. W. MACKEY: Mathematical Foundations of Quantum Mechanics (New York, N.Y., 1963).

(16) J. S. BENDAT: Principles and Applications of Random Noise Theory (New York, N.Y., 1968).

(17) H C. CORBEN and P. STEHLE: Classical Mechanics (New York, N.Y., 1950), p. 136.

(18) A model formally equivalent to this case has been independently described by G. C. SCALERA in a note to appear in Lett. Nuovo Cimento. Private commmnication.

(19) G. FARACI, S. NOTARRIGO and A. R. PENNISI: Nucl. Instrum. Methods, 165, 325 (1979).

(20) J. S. BELL: Comments At. Mol. Phys., 4, 121 (1980).

(21) A. ASPECT, J. DALIBARD and G. ROGER: Phys. Rev. Lett., 49, 1804 (1982).

(22) A. EINSTEIN: Mécanique quantique et réalité (reproduced in Ann. Found. De Broglie, 3, 81 (1978)).

(23) L. DE BROGLIE: Reflexions sur la causalité (reproduced in Ann. Fond. De Broglie, 2, 69 (1977)).

(24) E. SCHRÖDINGER: Are there quantum jumps? (reproduced in Ann. Fond. De Broglie, 2, 51 (1977)).

(25) K. R. POPPER: in Quantum Theory and Reality, edited by M. Bunge (Berlin, 1967), p. 7.

(26) M. BUNGE: in Quantum Theory and Reality, edited by M. Bunge (Berlin, 1967), p. 105.

(27) A. S. HOLEVO: Probabilistic and Statistical Aspects of Quantum Theory (North ­Holland Pub. Co., Amsterdam, 1982), p. 20.

(28) K. R. POPPER: Nature (London), 219, 682 (1968).

(29) L. E. BALLENTINE: Rev. Mod. Phys., 42, 358 (1970).

(30) C. TRUESDELL: Proc. S.I.F., Course XIV, edited by P. Caldirola (Academic Press, New York, N.Y., 1961), p. 21.

(31) D. G. HOLDSWORTH and C. A. HOOKER: A critical survey of quantum logic, in Logic in the 2Oth Century, Scientia, Suppl. to Vol. 116 and 117 (1981-1982), notes 3a, p. 204 and 24, p. 208.