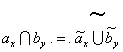Il linguaggio scientifico dei Presocratici

analizzato con l’ideografia di Peano

Salvatore Notarrigo

Preambolo

La lingua naturale è uno strumento essenziale per risolvere i problemi che l’uomo deve affrontare nel suo vivere sociale. Senza di essa non potrebbero esistere nè scienza, nè poesia, nè rapporti sociali e nemmeno chiacchiere inutili; in una parola, non potrebbe esistere la società. Ma proprio per tale ragione le lingue naturali, attraverso il loro lungo e contorto sviluppo nel corso della storia delle singole comunità linguistiche, vanno accumulando ambiguità, ridondanze, contraddizioni, paradossi.

Da ciò la necessità di creare gerghi particolari per determinate attività che a loro volta ed alla lunga contribuiscono ad aumentare la confusione nella lingua comune; e non a caso fin da tempi remoti si tramanda il mito della torre di Babele!

Un particolare gergo, creatosi all’interno di una qualche comunità, può assolvere il compito per cui s’è formato solo finché resta circoscritto a quella comunità ed allo scopo per cui è nato. Ma così facendo si chiude inesorabilmente all’interno di se stesso e muore con il cambiare delle condizioni al contorno relative alle attività per il cui scopo il gergo si era venuto formando; condizioni al contorno che a loro volta si vanno modificando anche per effetto dello stesso sviluppo sia dell’attività che dello stesso gergo.

La riprova di ciò è il fatto che tutti i tentativi di creare una lingua universale, come l’esperanto o il latino sine flessione di Peano, ecc., sono miseramente, ma necessariamente, falliti.

Qualche volta il gergo resiste solo perché si è venuto trasformando in un coacervo di dogmi che, pur avendo perso ogni significato reale, hanno strutturato in qualche modo la comunità che lo usa; trasformandola alla fine in una setta che continua a scambiarsi messaggi che ormai risultano incomprensibili ai suoi stessi membri; per cui il gergo assume la sola funzione di mantenere i rapporti gerarchici che si sono stabiliti all’interno di essa.

Anche nella matematica e nella logica, la cui essenza proprio consiste nella corretta manipolazione di simboli, si è verificato il fenomeno prima considerato e nel corso della loro storia è stato necessario rivoluzionare tutto per conseguire reali progressi; per cui, come giustamente notava il Peano, la storia della matematica e quella della logica praticamente coincidono con la storia dei loro simboli.

Ma non necessariamente il cambiamento è dovuto all’esigenza di progredire perché spesso gli interessi costituiti di determinati settori della società impongono il cambiamento proprio allo scopo di impedire una rivoluzione. E non è mai stato facile distinguere la rivoluzione dalla reazione; anche se ognuno ritiene di essere in grado di farlo; anche se poi scopre che la sua particolare bipartizione è diversa da quella degli altri; ma la cosa, in genere, non lo preoccupa minimamente perché è sempre pronto a ritenere che gli altri o sono in malafede o sono dei semplici imbecilli.¹

Solo a poche persone è riservata la capacità di distinguere senza farsi distogliere da pregiudizi di parte.

Uno dei rari esempi tra questi è l’aristocratico Tomasi di Lampedusa il quale fa dire, durante l’avanzare della classe borghese, a uno dei suoi aristocratici personaggi che bisognava cambiare qualche cosa perché tutto potesse rimanere come prima!

***

Poiché il fenomeno di cui stiamo parlando, cioè l’instabilità dei gerghi, è, al contrario, estremamente stabile, necessariamente deve esistere un meccanismo sottostante che lo regola (per evitare equivoci chiariamo che il termine “instabilità” viene qui usato nel senso tecnico della teoria matematica dei sistemi complessi e cioè nel senso di una situazione che per un certo tempo si muove così lentamente da apparire praticamente ferma finché non incontra un punto di “catastrofe” che ne cambia radicalmente l’aspetto qualitativo).

In generale, per scoprire un meccanismo, bisogna prima ridurre il fenomeno ai suoi elementi fondamentali ed alle forze che li sospingono. Per tale ragione, in modo nè esaustivo nè definitivo, distingueremo quattro aspetti del linguaggio e due forze contrastanti alle quali però va sempre aggiunto il principio generale dell’entropia.

Il primo aspetto è rappresentato dal linguaggio “pratico”; questo serve, in modo (più o meno) razionale, a risolvere tutti i problemi quotidiani e di routine. Il suo fondamento è costituito precipuamente dalla regola del provare e riprovare empiricamente cercando di correggere gli errori con la metodologia del caso per caso.

La forza che lo spinge è la “necessità della sopravvivenza”.

Ed è la stessa forza che anche lo spinge a creare un linguaggio più sintetico ma più potente, svincolato dall’empiria e dal caso per caso. Proprio per questa ragione esso dev’essere astratto e generale e tuttavia estremamente preciso e quindi capace di affrontare situazioni nuove, mai prima sperimentate. Questo costituisce il secondo aspetto e cioè il linguaggio “scientifico”.

Tale forza in avanti automaticamente crea la sua controreazione (la “necessità del progresso”): infatti l’estrema precisione del linguaggio scientifico crea una specie di prigione che impedisce qualsiasi evoluzione. A ciò contribuiscono le Vestali che presto o tardi, magari proprio quando esso ha perduto ogni sua funzione, si costituiscono a custodi delle regole del linguaggio che perciò da funzionali diventano ferree. Per uscire fuori dalla prigione occorre volare via spaziando con estrema audacia nel regno dell’ignoto o comunque del non ancora ben noto.

E così si viene a creare il linguaggio “poetico”, terzo degli aspetti sopramenzionati.

Dallo scontro di queste due forze uguali e contrarie si genera il quarto aspetto del linguaggio e cioè quello delle “chiacchiere inutili”.

Queste non contribuiscono menomamente al progresso ma lo ostacolano; e non contribuiscono alla sua precisione ma ne aumentano la confusione e servono solo ad erigere la torre di Babele.

La causa di ciò è il principio generale dell’“entropia”: la necessità della precisione, insieme ai veri scienziati, tende a produrre il fenomeno negativo delle Vestali o falsi scienziati; d’altronde, la necessità del progresso porta seco, insieme ai veri poeti, gli istrioni o falsi poeti.

Vestali ed istrioni vengono, spesso a loro insaputa, rimescolati ed usati dalla necessità della pratica che, nel frattempo trasformatasi in interessi costituiti, sfruttando le spinte contrastanti dei microinteressi individuali o corporativi diventa la sola legge imperante.

E, allo stesso modo di come si verifica in termodinamica statistica, la legge del caso trasforma un sistema deterministico ma reversibile in un sistema ancora deterministico ma apparentemente casuale ed irreversibile. Venendosi così a confermare il principio generale dell’entropia secondo il quale i sistemi isolati devono marciare inesorabilmente dall’ordine verso il disordine.

E tuttavia le chiacchiere inutili hanno una grande funzione sociale in quanto, anche se “in sé” non significano niente, servono ad unire i simili con i simili; creando così le varie chiese, o corporazioni, o consorterie.

Attraverso queste, molte “CHIACCHIERE INUTILI” vengono pomposamente ribattezzate “LA SCIENZA” e “LA POESIA”.

Di tanto in tanto, tuttavia, emergono i geni che, rifacendosi alle conquiste del pensiero passato, ma ormai sepolto dalle infinite diatribe tra falsi scienziati e falsi poeti (cumulativamente li chiameremo falsi profeti!), tendono a procurare qualche avanzamento; ed in minima parte vi riescono lasciando la loro traccia; anche se, subito dopo, i falsi profeti tendono ad annebbiare tutto di nuovo (magari abusando del nome degli stessi geni che vengono trasformati, ormai che sono morti e non possono più reagire, in santoni) proclamando il “nuovo” verbo, che ormai falsato, non si riesce più a distinguere da quello “vecchio” che preesisteva al genio; e, arrogandosi il diritto di diffondere questo “nuovo” vangelo e distribuendosi le cariche di vescovi e di papi, giudicano inappellabilmente di chi tra i fedeli sia un ortodosso o un eretico.

Per tale scopo i falsi profeti hanno la necessità di forgiarsi la teoria delle PULCI (cioè del “Progresso Universale Lineare Continuo Infinito”); quando, al contrario, la storia rivela un caotico succedersi di avanzate e retrocessioni che spesso rasentano di nuovo lo zero assoluto! Ma la teoria del progresso ininterrotto è molto comoda e difficile da abbandonare; con tale teoria viene permesso infatti ad un moderno, anche se imbecille, di avere sempre ragione su di un antico, anche se un genio; allo stesso modo dei grandi che pretendono di avere sempre ragione sui bambini, nonostante la sequenza temporale è, nel nostro caso, invertita.

Notiamo che l’apparizione dei geni non contraddice l’analogia termodinamica in quanto quest’ultima scienza prevede anche situazioni lontane dall’equilibrio in cui la riduzione del contenuto entropico del sistema si ottiene a spese di sorgenti esterne o sfruttando riserve precedentemente accumulate in una parte di un sistema più ampio (pensiamo alle riserve di combustibili della terra come sistema più ampio della biosfera).

Nel caso del linguaggio scientifico l’esterno è rappresentato dai contatti con altre culture e le riserve si trovano nascoste nelle biblioteche sotto forma di libri che nessuno ha mai letto perché non servono al paradigma dominante e di tanto in tanto anzi si provvede con qualche incendio ad arrestare l’incombente pericolo della scienza (questa volta scritta in minuscolo!) che farebbe sgonfiare tutti i palloni che a forza erano stati gonfiati.

Si dice che il califfo Omar, ritenuto l’ennesimo incendiario della biblioteca di Alessandria, abbia detto per spiegare (naturalmente non per giustificare!) il suo operato: Se i vostri libri dicono le stesse cose che dico io allora sono inutili; se dicono cose diverse allora sono dannosi.

***

Nelle discussioni sulla scienza e quindi sul suo linguaggio si sono fatte molte chiacchiere, data la sua enorme rilevanza sociale. Ai nostri fini menzioneremo solo due problemi sui quali lungamente si è dibattuto.

Il primo riguarda la nascita della scienza, il secondo la sua evoluzione. Per entrambi si sono sostenute tesi contrapposte. Nasce la scienza dalle esigenze pratiche e dal perfezionamento del lavoro tecnico o non piuttosto dalle religioni e dai miti?

La prima tesi viene prevalentemente sostenuta da coloro che si mettono in posizione critica nei confronti del sistema; per costoro gli attori del processo di creazione della scienza sono ovviamente i lavoratori; da questi si formano i tecnici e da questi, a loro volta, emergono gli scienziati. La formazione dei sacerdoti o bramini della scienza sono un fatto involutivo dovuto a cause sociali esterne. I sostenitori di tale tesi tendono a rispondere al problema dell’evoluzione della scienza ricorrendo a cause “esterne” e cioè alla struttura sociale.

La seconda tesi viene sostenuta principalmente dagli apologeti del sistema; naturalmente per costoro la scienza nasce dal mito e dalla religione; gli attori del processo sono i sacerdoti che hanno il tempo sufficiente per occuparsi di cose che vanno oltre le necessità immediate. Il problema dell’evoluzione della scienza viene quindi risolto ricorrendo alla dinamica “interna” della scienza che trascende i mutamenti delle strutture sociali. Se una società viene distrutta o si autodistrugge, la scienza, come anima immortale, si trasferisce altrove e continua a crescere indisturbata.

Ma non sono solo questi ultimi a sostenere quella che abbiamo chiamato la teoria delle PULCI, anche i primi la sostengono. Entrambi per sostenerla sono costretti a mutilare la scienza: i primi, identificando praticamente la scienza con la tecnica, guardano all’accumularsi delle conoscenze tecniche e trascurano quasi totalmente, almeno nei fatti, gli elementi teorici che sotto il nome di ideologia vengono semplicemente derisi; spesso buttando via il bambino insieme all’acqua sporca. Stranamente, poi, l’identificazione della scienza con la tecnica viene invece diffusa tra le masse proprio dai detentori del potere economico dopo averne operato solo una piccola, ma non neutrale e non senza conseguenze, sostituzione: il lavoro viene sostituito con la grande industria come motore delle conoscenze scientifiche.

Gli apologeti del sistema, invece, per mutilare la scienza sono costretti a mutilare la storia, classificando come barbari ed incolti tutti i popoli che non stanno dentro il paradigma, inventandosi capziose provenienze culturali; come p. es. gli “europei” hanno fatto con la cultura greca: tagliando completamente fuori tutte le filosofie medioevali da cui più propriamente la nostra cultura immediatamente deriva e gettando un diretto ma impossibile ponte verso la scienza greca.

La nostra idea è che entrambe queste tesi siano parziali e adialettiche.

Come si verifica in tutti i sistemi complessi, e la cosa ha una spiegazione matematica, si hanno consecutivi rami evolutivi, qualitativamente diversi, e intervallati da punti di diramazione con caratteristiche catastrofiche tali da annullare quasi tutto quello a cui precedentemente si era dato il nome di scienza. In ogni punto di diramazione si aprono altri rami possibili, che il futuro potrebbe in teoria percorrere, diversi tra loro dal punto di vista qualitativo; l’imboccare l’uno o l’altro ramo dipende da fattori “esterni” quasi esclusivamente di natura economica e sociale.

A partire da tale punto di instabilità, superata la fase iniziale, in cui ogni volta si riparte praticamnente da zero, il sistema socio-economico-culturale si stabilizza; anche sviluppando meccanismi di autoprotezione, e procede con un’inflessibile logica “interna” fino a che le forze entropiche non lo distruggeranno di nuovo quando si sarà raggiunto il prossimo pulito di diramazione.

In questo scritto vogliamo, in un primo momento, descrivere l’evoluzione del linguaggio scientifico tra due successivi punti catastrofici e per concretezza il materiale empirico lo prenderemo dalla storia dell’evoluzione del pensiero scientifico nato, quasi contemporaneamente, nella Ionia e nell’Italia di alcuni millenni fà. Questo per due ragioni: l’una è che tale periodo storico è abbastanza lontano nel tempo, riducendo così la probabilità (anche se non la possibilità!) di lasciarci coinvolgere completamente nelle passioni ideologiche; l’altra ragione è che questo periodo della storia della cultura è sufficientemente documentato per poterne azzardare una descrizione teorica.

Per fare questo, senza incorrere nel sempre presente pericolo delle chiacchiere inutili sarà prima necessario costruirsi gli strumenti adatti.

Anche se tali strumenti sono stati usati, spesso con grande maestria, fin dai tempi di Pitagora e, molto probabilmente anche prima, il loro perfezionamento e la riflessione su di essi è opera molto recente e quasi esclusivamente dovuta a Peano ed alla sua scuola.

A tal riguardo potrebbe apparire strano il fatto che tale scuola sia oggi quasi completamente dimenticata ed al suo posto si sia affermata una sua derivazione distorta ed assurda (come andremo notando nel seguito) iniziata dal Russell; ma alla luce delle considerazioni precedenti il fatto, più che strano, appare invece assolutamente naturale e difficilmente si sarebbe potuto immaginare il contrario (vedi in proposito l’articolo di Boscarino in questo stesso numero dei Quaderni che sarà indicato nel seguito colla sigla PF).

L’ideografia di Peano

Dal momento che, oggi, l’ideografia di Peano è praticamente sconosciuta ed i simboli da lui inventati vengono usati con significati del tutto diversi o, comunque, distorti e poiché essa avrà un ruolo fondamentale per sviluppare il nostro discorso, questa sezione ad essa dedicata assumerà, necessariamente, una forma piuttosto didascalica.

Dal punto di vista filosofico, i contributi fondamentali di Peano alla scienza della logica (non considerando i molti ed importantissimi contributi da lui apportati dal punto di vista più specificatamente tecnico) sono due: la distinzione tra i diversi significati che si nascondono sotto l’unico termine rappresentato nella lingua comune dal verbo “essere” ed il chiarimento concettuale dei termini fondamentali e del significato di quello che oggi si chiama un “sistema deduttivo”.

Cercheremo di capire, in questa sezione, l’essenza di tali contributi straordinari ed estremamente fecondi.

Consideriamo le seguenti “proposizioni” della lingua italiana:

1) Mongibello è l’Etna.

2) Il mais è granoturco.

3) L’Etna è il vulcano pitì alto.

4) Socrate è mortale.

5) Socrate è un uomo.

6) Aristotele è un uomo.

7) L’uomo è mortale.

8) Il cane è un animale.

9) Qualcosa é mortale.

10) Qualcuno é mortale.

Secondo la logica grammaticale, le dieci proposizioni sono tutte della forma: soggetto, copula, predicato.

Al contrario, i loro “significati reali” (cioè quello che effettivamente significano, indipendentemente dalla forma nella quale sono state espresse) sono tutti diversi.

Tuttavia, dal punto di vista della “logica”, alcune hanno “significato formale” (cioè la forma logica in cui sono espresse, indipendentemente dal loro, eventuale, significato reale) identico ed altre, invece, diverso:

Nella 1), i “termini” a sinistra e a destra della copula sono entramnbi degli “individui” ²

Nella lingua italiana gli individui sono, generalmente, rappresentati da nomi propri (propri ad un solo e ben determinato individuo).

Nella 2), i “termini” a sinistra e a destra della copula sono entrambi delle “proprietà”.

Nella lingua italiana le proprietà sono, generalmente, rappresentate da nomi comuni (comuni a più individui).

E, tuttavia, le 1) e 2) hanno qualcosa in comune che li distingue formalmente dalle altre. Infatti, in entrambe, si intende dire che i due termini a sinistra e a destra della copula, anche se diversi tra loro, hanno “identico” significato (reale); in altre parole, sono due nomi diversi per la stessa cosa; il che implica che l’un termine si può sostituire all’altro, e viceversa, in ogni contesto in cui compaiano; purché detti termini intendano riferirsi ai loro significati e non ai “segni” stessi.

Per esempio, se dico “mais ha quattro lettere” non posso sostituire al termine “mais” il termine “granoturco”. E non posso sostituire “mais” a “granoturco” nella proposizione:

“granoturco è una parola composta dalle due parole grano e turco”.

Possiamo convenire di scrivere, al posto della copula, il “segno” “ =” e così le 1) e 2) diventano:

Mongibello = Etna

mais = granoturco

secondo lo “schema di proposizione”:

(F1) a = b,

da leggere: “a” è identico a “b”; ovvero “a” significa “b”; dove “a” e “b” sono due “simboli” che rappresentano due termini generici. Cioè termini dotati di un significato (e di uno solo) ma che non ci interessa di sapere perché noi siamo interessati solo alla relazione che li lega, denotata dal segno “=”.

Nelle 3), 4), 5), 6), invece, a sinistra ci sta un individuo e a destra una proprietà. Questo basterebbe a dirci che la copula, in questo caso, non può significare l’identità dei due termini. Di fatto, in queste proposizioni, si vuole intendere che a sinistra della copula ci sta un individuo che ha la proprietà nominata a destra.

Converremo, in questo caso, di indicare la copula semplicemente con il segno “Δ e scrivere:

Etna Î vulcano più alto

Socrate Î mortale

Socrate Î uomo

Aristotele Î uomo.

Secondo lo schema:

(F2) a Î b,

da leggere: “a” è un “b”’ ovvero: l’individuo “a” ha la proprietà “b”.

Nelle 7) e 8), a sinistra e a destra della copula ci sono due proprietà, come nella 2), ma i due termini non sono reciprocamente sostituibili in quanto il primo esprime un concetto che è parte del secondo; o, in altre parole, la prima proprietà implica la seconda ma non viceversa.

Per quest’altro significato del verbo essere, useremno il segno “É” secondo lo schema:

(F3) a É b,

che leggeremo: la proprietà “a” implica la proprietà “b”, ovvero la proprietà “a” include la proprietà “b” o, ancora: gli individui che hanno la proprietà “a” sono inclusi tra gli individui che hanno la proprietà “b”.³

Infine, nelle 9) e 10), a sinistra della copula ci sono degli individui e a destra delle proprietà, come nelle 3), 4), 5) e 6), ma l’individuo non è rappresentato da un nome proprio ma da un pronome indefinito che, quindi, indica un individuo generico e le proposizioni, più che asserire qualcosa sugli individui, asseriscono qualcosa sulle proprietà stesse.

In particolare, con la 9) si asserisce che la proprietà “mortale” non è una proprietà assurda, cioè senza individui che la possano avere; ma, al contrario, non è affatto impossibile l’esistenza di individui che hanno la proprietà di essere mortali.

Con la 10) si vuole dire la stessa cosa, solo che, nell’accezione comune, il termine “qualcuno”, a differenza di “qualcosa”, vuole indicare un “uomo”; per cui la 10) si potrebbe esprimere con, “qualcosa è uomo e mortale”. Se indichiamno con il segno “∩” la congiunzione “e”, si può formare la “proprietà composta”: uomo ∩ mortale e la 10) si riconduce allo schema 9) che possiamo simbolizzare con:

(F4) $ a ,

dove “a” rappresenta una proprietà (eventualmente, anche composta), ed il segno “$” indica che possono esistere individui che hanno tale proprietà.

La (F4) si può leggere: vi sono degli “a” o, anche, vi è almeno un «a», ecc.

Le (F1), (F2), (F3), (F4) individuano quattro significati diversi del verbo essere che è necessario distinguere formalmente in un sistema deduttivo per evitare conclusioni assurde a partire da determinate premesse.

Può essere talvolta utile esprimere anche le (F1), (F3), (F4) sotto la forma della (F2), cioe: soggetto, copula, predicato.

Ciò si può ottenere stipulando opportune convenzioni:

Se conveniamo di indicare con il segno “ι” la proprietà di essere “identico a” qualcosa, allora formalmente le (F1) ed (F2) si possono esprimere con la “formula”:

(F1’) a Î ι b,

che si può leggere: “a” è identico a “b” (cioè, “a” ha la proprietà di essere identico a “b”).

Intendendo, quindi, che i termini logici “=” e “Î ι ” hanno lo stesso significato. Cioè il segno “=” è un’abbreviazione dei due segni accostati “Δ e “ι ”.

Cioè:

(A1) = .=. Î ι

Notiamo che nella (A1) i due segni “ = ” e “. = .” hanno lo stesso significato reale ma un diverso significato formale, in quanto il primo appartiene al linguaggio simbolico che si ha intenzione di costruire (“linguaggio oggetto”); mentre il secondo appartiene al linguaggio che, necessariamente, dobbiamo usare per costruire il primo (“metalinguaggio”).

Se conveniamo di indicare con il segno “ á ” la proprietà di implicare la proprietà “b” (quindi “ áb ” è una “proprietà di proprietà”) , possiamo scrivere:⁴

(F3’) a Î áb .

Si può, quindi, asserire:

(A2) É .=. Î á .

Nella (F3’), la proprietà “a” assume la funzione logica di “individuo” rispetto alla proprietà di secondo livello “ áb ” .

Quindi se ne deduce che i concetti di individuo e di proprietà, tranne casi particolari, hanno valore relativo e non assoluto; cioè se un termine ha il ruolo di proprietà in una determinata proposizione essa può assumere il ruolo di individuo in un’altra, come in: Socrate Î mortale e mortale Î proprietà.

Anche la (F4) può essere messa nella forma (F2); per far ciò conviene introdurre la “proprietà assurda” che non può essere posseduta da alcun individuo e rappresentata dal segno “Ù”.

Con l’uso di tale segno si può esprimere l’idea che una data proprietà “a” è assurda o contraddittoria scrivendo:

(F5) a = Ù

che per la decoposizione dell’identità si può scrivere:

(F6) a Î ι Ù

che si può anche leggere: non possono esistere individui che possiedono la proprietà “a”.

Se conveniamo di usare il segno “ ~ ” per negare una proprietà, cioè per indicare la proprietà complementare della proprietà data, (nel nostro caso, la “ι Ù”, cioè la proprietà di essere identica alla proprietà assurda) potremo scrivere:

(A3) $ a .=. a Î ~ ι Ù .

cioè: dire che vi sono degli “a” è la stessa cosa che dire che la proprietà “a” non è identica alla proprietà assurda.

È importante notare che l’idea di “esistenza” in logica coincide con l’idea di “esistenza possibile”. Altri significati del termine sono propri delle scienze empiriche e devono essere descritti e menzionati esplicitamente come particolari proprietà di determinati individui.

Notiamo, ancora, che la distinzione tra i significati del verbo essere espressi dai due termini logici “Δ e “É” è di estrema importanza; in quanto, oltre ai diversi significati reali, i due segni hanno proprietà formali molto diverse tra loro.

Infatti consideriamo le due proposizioni seguenti:

0a) Socrate è mortale,

0b) gli italiani sono dotti.

Il verbo essere nelle due frasi precedenti ha un significato logico diverso come si può subito mostrare.

Notiamo prima che, tra gli innumerevoli altri, ci sono due modi diversi per negare le due frasi:

1a) non vero che Socrate è mortale,

2a) Socrate è immortale (= non mortale);

1b) non vero che gli italiani sono dotti,

2b) gli italiani sono ignoranti (= non dotti).

Le proposizioni 1a) e 2a) hanno ovviamente lo stesso significato (a meno che non si cambi il significato di immortale riferendosi, come spesso si usa, non all’uomo ma alla sua opera od al suo nome); mentre, altrettanto ovviamente, le 1b) e 2b) hanno significato diverso.

La 1b) ci dice che possono esserci degli italiani che sono ignoranti ma non nega che ci possano essere degli italiani dotti; la 2b) invece nega esplicitamuente anche questa seconda possibilità. Spesso per evitare ambiguità si preferisce dire al posto della 1b): non vero che tutti gli italiani sono ignoranti.

Tutto questo ci fa vedere che il verbo essere, nei due casi 0a) e 0b), assume significato diverso; infatti non è possibile pensare che ammesso, per ipotesi assurda, che abbia lo stesso significato si debba comportare in modo diverso quando le due proposizioni vengano sottoposte alle stesse possibili operazioni di negazione.

Esprimeremo le frasi precedenti in modo più preciso con:

0a’) Socrate Î mortale,

0b’) italiano É dotto,

1a’) Socrate ~ Î mortale,

2a’) Socrate Î ~ mortale,

1b’) italiano ~ É dotto,

2b’) italiano É ~ dotto.

Abbiamo abbreviato con i segni “~ Δ e “~ É” la negazione delle relazioni⁵ “Δ e “ É” rispettivamente (il che equivale a negare le proposizioni stesse nella loro globalità); e con i segni “Î ~” e “É ~” la negazione dei soli termini di destra della proposizione, cioè mortale e dotto rispettivamente.

Si può quindi scrivere in modo generale ed astratto, cioè formale:

~ Î .=. Î ~

Cioè:

i segni “ ~ Î ” e “ Î ~ ” hanno lo stesso significato.

E, d’altra parte:

~ ( ~ É .=. É ~ ) .

Le parentesi servono solo ad indicare che il primo “~” si riferisce a tutta la proposizione, compresa tra le due parentesi, retta da “.=. ” .

Si può evitare l’uso delle parentesi scrivendo:

~ É . ~ =. É ~ ;

o, più semplicemente, abbreviando: “ ~ = ” con il segno “¹” :

~ É . ¹ . É ~ .

Cioè le ultime tre, con segni diversi, dicono tutte che:

non è vero che “ ~ É” e “ É ~ ” hanno lo stesso significato

o equivalentemente:

“ ~ É” .non significa. “ É ~ ” .

Può risultare utile fare anche le abbreviazioni “Ï” al posto di “ ~ Î ” e “” al posto di “~ É” scrivendo:

Ï .=. ~ Î .=. Î ~

ed invece si avra:

.=. ~ É . ¹ . É ~

In matematica si dice brevemente che la coppia di segni “~” e “Δ gode della proprietà commutativa mentre per la coppia “~” e “ É” tale proprietà non vale.

Un’altra importante diversità formale tra i segni “Δ e “É” si può notare dai seguenti esempi:

dalle asserzioni

“l’uomo è mortale”

e

“ogni mortale è un essere vivente”

segue necessariamente l’asserzione:

“l’uomo é un essere vivente” (sillogismo).

O, detto in modo più preciso:

“uomo É mortale” e “mortale É essere vivente” implicano: “uomo É essere vivente”.

O, in simboli: “(a É b) ∩ (b É c ) .É. (a É c)” ;

L’uso di “É” tra proposizioni, col significato di implica (come quello che nell’ultima formula sta tra i due punti), invece che tra proprietà, sarà chiarito in seguito.

I matematici dicono che la relazione “É” gode della proprietà transitiva. Proprietà che invece non vale per la relazione “Δ; infatti da “Socrate è mortale” e “mortale è una proprietà” non segue che “Socrate é una proprietà” o in scrittura più precisa: da “Socrate Î mortale” e “mortale Î proprietà” non segue “Socrate Î proprietà”.

Ancora, banalmente: mentre “É” gode della proprietà riflessiva, p.es.: “uomo É uomo”; non avrebbe alcun senso dire “uomo Î uomo” o “Socrate Î Socrate”; tuttavia potrebbe avere senso dire: “un uomoÎ uomo”: perché con il termine “un uomo” si vuole intendere un individuo generico del concetto di “uomo”, cioè, che ha la proprietà di essere “uomo”.

***

In un “sistema deduttivo” si deve distinguere tra “termini primitivi” di cui già se ne suppone noto il “significato reale”, e “termini derivati” di cui, invece, se ne dà una “definizione nominale”, a partire dai termini primitivi, mediante l’uso dei vari “termini logici”.

Una definizione nominale non dice niente sui significati reali dei termini definiti, almeno direttamente. Essa si riferisce solo ai nomi.

La forma più usuale è:

(F7) a . = . b,

dove “a” è il nuovo termine (o complesso di termini) da definire e “b” è il complesso di termini, di significato già noto, che danno il “significato formale” di “a” e, indirettamente, anche il suo significato reale a partire da quello proprio di “b”.

Un esempio è:

pentagono . =. poligono con cinque angoli.

Dove si suppone noto il significato reale di tutti i termini a destra dell’identità e si intende introdurre il nuovo termine “pentagono” come semplice abbreviazione dei termini a destra di “ . = . ” .

Il “significato reale” dei termini primitivi (o all’occorrenza, come ulteriore schiarimento, anche di quelli derivati) si può dare solo mediante una “descrizione”, eventualmente corredata da opportuni esempi.

Anche se è praticamente impossibile circoscrivere il significato di un termine, mediante una descrizione, in modo da ridurre a zero ogni ambiguità, tuttavia, nella pratica scientifica, si riesce a ridurre le ambiguità a limiti più che soddisfacenti.

Del resto, in modo del tutto spontaneo, quando un linguaggio scientifico si viene formando, i suoi utenti, anche se nel parlare comune attribuiscono significati diversi ai singoli termini, devono, all’interno del contesto della loro formalizzazione mettersi necessariamente d’accordo per restringerne il significato al loro nucleo comune; fermo restando che fuori dal contesto ognuno può dare ad essi il significato che più gli aggrada purché non affermi in questo caso di fare affermazioni scientifiche.

Senza che per questo si debba svalutare il linguaggio non scientifico; e questo non solo perché, come già detto nel Preambolo, si annullerebbe il valore della poesia la quale si basa essenzialmente sull’ambiguità dei termini (il cui scopo è quello di suggerire, attraverso i canali dell’emotività, significati pregnanti sul piano esistenziale) ma anche perché il linguaggio scientifico è troppo restrittivo e, usato indiscriminatamente, verrebbe a costituire una prigione e si trasformerebbe nel contrario della scienza stessa impedendo qualsiasi reale progresso scientifico. Una parola di moda che comprende anche questo fenomeno di sociologia della scienza è “paradigma”.

Si può quindi dire che il linguaggio scientifico serve per capire ed il linguaggio poetico serve per progredire; ma, dialetticamente, non si può progredire senza prima avere capito e non si può capire senza tentare di progredire. Ecco perché i veri scienziati sono anche in parte poeti ed i veri poeti sono anche in parte scienziati. Non a caso i grandi scienziati del nostro lontano passato scrivevano la loro scienza in versi poetici come Parmenide ed Empedocle, per citare solo quelli di cui ci sono pervenuti ampi frammenti.

***

Dopo che si siano definiti i vari termini e se ne sia ristretto il significato in modo da ridurre le ambiguità al minimo possibile, è bene, anche se non strettamente necessario, inventare per essi dei simboli adatti creando così un”’ideografia” cioè una corrispondenza biunivoca tra l’idea che si vuole rappresentare ed il segno introdotto.

Il procedimento che abbiamo descritto per restringere il significato dei termini del discorso costituisce, appunto, la descrizione del termine. Esso è l’unico modo possibile per assegnare al termine un significato reale (nel seguito, spesso, lo indicheremo semplicemnente con significato) in quanto distinto dall’eventuale suo significato formale (nel seguito, spesso, indicheremo quest’ultimo semplicemente con definizione). Appunto per questo, spesso, la descrizione viene anche chiamata definizione reale del termine, da distinguersi dalla definizione nominale che fa astrazione dal significato reale e ne dà invece il significato formale (vedi PF).

Poiché il segno, che viene formalmente introdotto per designare il termine, di cui se ne sia già data la descrizione, è in generale diverso dai più o meno corrispondenti termini del linguaggio comune sarà più facile evitare gli usuali slittamenti semantici che conducono a paralogismi ed a paradossi. Ed è per la stessa ragione che la corrispondenza tra idee e segni deve essere biunivoca (cioè ad ogni segno deve corrispondere un solo termine e viceversa); per cui nel linguaggio veramente scientifico non dovrebbero ammettersi nè omonimi né sinonimi; a meno di utili e non ambigue eccezioni, come quando — per quanto riguarda i sinonimi —possa risultare utile l’introduzione di un nuovo segno che stia come semplice abbreviazione di una più lunga sequenza di segni precedentementi introdotti, in tal caso si parla appunto di definizione nominale; come nell’esempio citato: “pentagono = poligono con cinque angoli” o per quanto riguarda gli omonimi — l’assegnare lo stesso segno a relazioni ed operazioni che siano correlate da una corrispondenza tra insiemi diversi di oggetti (cioè nei casi in cui i matematici parlano di isomorfismo o, più generalmente, di omomorfismo), finché non sorgano pericoli di ambiguità.

Anche una macchina, che sia in grado di riconoscere i segni che corrispondono alle lettere dell’alfabeto, può essere in grado di sostituire alla parola “pentagono” tutte le parole che lo definiscono (che stanno a destra del segno “=”) e viceversa; e ciò anche se non conosce menomamente il significato reale delle parole che tratta. Del resto è proprio per questo che un computer riesce a fare tutte quelle belle cose che tutti sanno, nonostante non capisca niente dei significati reali delle “parole” che elabora! Tuttavia tale “macchina” funziona molto meglio di qualsiasi uomo per quanto riguarda i significati formali appunto perché non è condizionato dai significati reali e bada solo alle regole di trasformazione che sono state memorizzate una volta per tutte nel suo programma e per di più è di gran lunga più veloce!

Il linguaggio del calcolatore, quello della logica formale e della matematica hanno questo in comune, cioè quello di realizzare il sogno di Leibniz attuato compiutamente dal Peano, di poter decidere ogni diatriba semplicemente dicendo “calculemus” e procedendo formalmente alle necessarie logiche deduzioni a partire dalle definizioni formali (cioè nominali) date e dagli assiomi anch’essi formalizzati ed esplicitamente presupposti.⁶

Tuttavia non è da pensare che il calcolatore possa fare della matematica o stabilire gli assiomi della logica; non foss’altro perché non ne capisce i significati reali; esso può solo effettuare dei calcoli, una volta che il matematico e/o il logico gli abbiano fornito definizioni, assiomi e regole di trasformazione; ed è per questo che non sbaglia! (naturalmente limitatamente al suo compito abbastanza ristretto che, per l’appunto, consiste in quello di “calcolare” o, più generalmente, di “elaborare”).

Il matematico ed il logico invece possono sbagliare perché non è facile individuare tali inputs per il calcolatore non essendo facile liberarsi da pregiudizi metafisici o di ogni altra natura; a parte l’osservazione banale che quello dei logici e dei matematici è (o almeno dovrebbe essere) un lavoro creativo e non di semplice elaborazione. Ne consegue che il calcolatore può fare quasi tutto, anche dimostrare teoremi, ma non può sostituire il matematico; e può fare financo le poesie ma non certamente potrà fare mai il poeta! Naturalmente finché non si voglia ridefinire il ruolo di matematici e poeti come spesso avviene e ciò capita, e non di rado, anche a tali medesimi attori come si desume leggendo certe loro enunciazioni o guardando a certe loro pratiche.

***

Esempi di definizioni reali sono appunto quelli che abbiamo dato “descrivendo” il termine definizione nominale e quelli che andremo facendo per descrivere il termine stesso di definizione reale. In modo più formale, possiamo “descriverle” così: Supponiamo di voler descrivere un termimie che chiameremo “x”, supponiamo che “a”, “b”, “c”, “d”, “e”, “f”, ecc., siano delle proprietà di cui, anche se in modo non privo di ambiguità, ne conosciamo già il significato; allora cominciamo a precisare che: “x” e un “a” o un “b” ed è anche un “c” ma può essere anche un “d” o un “e” ma non è un “f”. E così seguitando, in modo più o meno analogo, usando le particelle “é un”, “e”, “o”, “non”, ... , o altre particelle che abbiano la stessa funzione, cioè quella di connettivi operanti tra le varie proprietà di partenza; e adducendo, eventualmente, opportuni esempi.

Ma già possiamo notare che le particelle: “è un”, “ed”, “o”, “ma”, “non” ecc. sono anch’esse dotate di una notevole dose di ambiguità. Infatti, quando usiamo la disgiunzione “o” inserita tra le proprietà “d” ed “e”, la dobbiamo intendere in senso inclusivo o in senso esclusivo? o, in altre parole, intendiamo riferirci ad una qualunque delle tre possibilità, per “x”, di essere: un “d” senza essere un “e”, un “e” senza essere un “d” o, anche, un “d” e nello stesso tempo pure un “e”? oppure vogliamo escludere l’ultima possibilità cioè che “x” possa avere entramnbe le proprietà “d” ed “e” insieme?

E la stessa congiunzione “e” (o “ed”) che significa?

Spesso nella lingua comune la si usa col sigmiificato della “o” inclusiva, come quando al botteghino del teatro incontriamo un cartello con su scritto: Riduzione per militari e studenti.

Certamente si vuole dire che per avere la riduzione bisogna essere o militari o studenti o entrambe le cose; e non certo che bisogna essere contemporaneamente sia militari che studenti, cioè studenti che fanno il militare o militari che sono studenti.

Dell’ambiguità di “ è un ” abbiamo già detto.

Allora per evitare ambiguità scriveremo un segno speciale per ogni possibile significato, evitando i pericoli dell’omonimia; p.es:

“U” per la disgiunzione inclusiva,

“∩” per la congiunzione,

“~” per la negazione, ecc.

Poi, potremmo scoprire che i segni introdotti non sono tutti indipendenti e che alcuni di essi si possono definire, questa volta nominalmente, come combinazioni degli altri; p.es. la disgiunzione esclusiva si può rendere con la formula: “(d ∩ ~ e) U (~ d ∩ e)”; cioè: “d” e non “e” o non “d” ed “e”. Risparmiandoci, in questo modo, l’introduzione di un nuovo segno. (Per ragioni puramente estetiche nella presentazione grafica delle formule scriveremo qualche volta, “” al posto di “~a”; per cui la formula precedente diventa “”).

Daremo ora alcuni significati reali di termini che useremo in seguito; altri (spesso in nota) li daremo al momento opportuno, a meno che non emergano chiaramente dal contesto. Ovviamente, assumeremo noti (almeno approssimativamente) i significati delle parole che useremo per “descriverli”. Il risultato finale potrebbe risultare diverso da quello a cui siamo abituati. Ma poco male, se abbiamo guadagnato in precisione potremo sopportarne il sacrificio. Naturalmente, se è alla precisione che siamo interessati! Ma purtroppo senza precisione semantica non si può “dedurre” un bel niente ma si potrà fare solamente una gran confusione.

Chiameremo “segno” un singolo atto della percezione sensibile, indipendentemente dal fatto che tale atto abbia per noi umi significato o meno; quindi anche uno scarabocchio o un rumore qualsiasi sarà per noi un “segno”. (Nel dizionario tale significato è incluso tra i possibili ma non è il solo e nemmeno quello originario o etimologico).

Chiameremo “termine” un segno che invece abbia per noi un significato ben definito come: Socrate, uomo, animale, “u”, ecc. Quindi, secondo le superiori descrizioni, tutti i “termini” sono “segni”, ma non tutti i “segni” sono “termini”.

Chiameremo “simbolo” un segno dotato sì di significato ma non fissato; cioè si suppone che il segno abbia un significato ma non ci interessa di conoscerlo. Come nell’operazione formale “d U e” in cui si suppone che i simboli “d” ed “e” abbiano un significato ma non ci interessa di conoscerlo perché noi siamo interessati, invece, solo alla loro relazione formale individuata dal termine “U”.

Spesso si indicano con i segni “costante” e “variabile” i significati che noi invece abbiamo attribuito ai segni “termine” e “simbolo”. Noi lo eviteremo perché si sono dimostrati ambigui. Non siamo sicuri che la nostra scelta potrà risultare migliore ma, al momento, la giudichiamo tale. Sarebbe bene inventare dei segni del tutto nuovi e convenzionali, ma quasi sempre, come già adombrato nel Preambolo, una precisione eccessiva riduce la facilità di comprensione immediata e questo, alla fine, potrebbe provocare l’effetto opposto.

Per tutti i termini che abbiamo descritto, comunque, la confusione è, attualmente, massima anche nel linguaggio della logica, per non parlare degli altri linguaggi scientifici; quindi non c’è soverchio pericolo nell’usare un nome con un significato particolare, purché convenientemente “descritto”.

Useremo il termine “proprieta” come sinonimo di “predicato”, di “nome comune”, di “attributo”, di “aggettivo”, ecc.

Useremo, invece, il termine “individuo” come sinonimo di “cosa”, di “oggetto”, di “nome proprio”, ecc.

Naturalmente con l’intesa che i termini precedenti devono essere usati nei significati appropriati, cioè quando i termini sopraelencati rappresentino effettivamente dei sinonimi, quindi, devono essere usati con quel significato che è l’intersezione di tutte quelle proprieta alle quali nella lingua comune si fa riferimento usando tali termini, come abbiamo chiarito nel descrivere le “descrizioni”.⁷

Come già detto, questo è l’unico modo con cui si può restringere il significato di un dato termine, data l’ambiguità del linguaggio naturale.

Abbiamo chiamato tale processo la descrizione o definizione reale del termine.

Per esempio, come notava il Padoa, illustre collaboratore di Peano, non potremo mai ottenere il significato reale del termine “significa” mediante una sua possibile definizione nominale perché dovremmo scrivere:

significa .significa. (un certo complesso di segni).

E, una volta trovato tale complesso di segni che definisce la parola “significa”, ne avremmo già dovuto conoscere il significato per poterlo riferire alla seconda apparizione di “significa”. In altre parole, il formalismo della logica non si occupa di significati ma solo di relazioni formali tra termini dotati di significato. Anche se molti sembrano pensare esattamente il contrario e cioè che si occupi del significato di relazioni formali tra termini senza significato!

Abbiamo scritto delle frasi come:

a) Socrate Î mortale, uomo É mortale, mais = granoturco,

ma anche delle formule come

b) x Î a , x É a , x = a .

Nelle a) compaiono oltre ai termini logici “Î, É, =” anche i termini extralogici“Socrate, uomo, mortale, mais, granoturco”.

Queste sono proposizioni con un valore semantico ben definito e non fanno parte della logica.

Le formule b) invece sono proprie della logica la quale tratta solo schemi formali che stanno per proposizioni arbitrarie. Quando sarà necessario essere più precisi li chiameremo schemi di proposizioni invece che proposizioni. Peano li chiama proposizioni condizionali per distinguerle dalle prime che chiama proposizioni categoriche. La terminologia attuale è varia.

Quindi, negli schemi di proposizioni, “oltre” ai termini logici compaiono “solo” dei simboli, che non hanno significato definito, espressi usualmente con singole lettere minuscole dell’alfabeto (possibilmente dotate di indici); ma tali simboli non sono senza significato; ché uno necessariamente lo devono avere anche se al formalismo della logica non interessa conoscerlo; gli basta sapere che uno (ed uno solo!) ce l’abbiano. Tali simboli, come già detto, vengono chiamati (tradizionalmente ma non molto opportunamente) variabili.

Il nome variabile è poco opportuno perché, preso alla lettera, potrebbe significare che noi potremmo effettuare, lungo il corso d’un ragionamento, degli slittamenti semantici per cui dalla formula sillogistica: “a É b” e “b É c” implica “a É c”, potremmo concludere assurdamente: Elisei É venti e venti É numero implica Elisei É numero; cioè dal momento che gli Elisei sono venti e venti è un numero ne segue che gli Elisei sono un numero!

Anche formule del tipo “x Î numero” o simili, cioè quelle in cui compaia un qualunque termine extralogico, non fanno parte della logica anche se possono fare parte di altre scienze formalizzate come l’aritmetica. Nei libri di logica, di tradizione russelliana che poi sono la stragrande maggioranza, questa regola non viene osservata arrivando a conclusioni paradossali, perché si mantiene l’illusione che tutto, ed in particolare l’aritmetica, sia riducibile a logica; identificando la logica con la metafisica, come è chiarito in PF.

Non è necessario nemmeno menzionare (nell’assiomatizzazione della logica) i termini proprietà ed individuo e non interessa nemmeno conoscerne il significato, ammesso che ne abbiano alcuno oltre quello formale.

Il decidere se hanno un significato non puramente formale non è una questione di facile soluzione essendo un problema di metafisica.

Non stiamo usando tale ultimo termine nel suo senso deteriore ma semplicemente per dire che la questione non è risolvibile né con la logica, né empiricamente; ma che bisogna necessariamente ricorrerre a postulati preliminari di ordine teoretico dei quali, nel costituire qualunque scienza, logica compresa, non si può fare assolutamente a meno.

Ciò costituisce la più grande costernazione dei neopositivisti che, pur di non ammettere questa banale verità, finiscono con lo scambiare la peggiore metafisica con le scienze, empiriche o formali che esse siano.⁸

***

Dal punto di vista puramente “formale”, cioè puramente “logico”, possiamo (meglio “dobbiamo”) fare finta di non conoscere il significato che tali termini hanno nel linguaggio comune e dire che è una “proprietà” qualunque cosa che venga rappresentata da un “segno”, qualunque ne sia il suo significato (purché ne abbia uno e uno solo!), che stia a “destra” di “Δ, ed è invece un “individuo” ciò che è rappresentato da un “segno”, qualunque ne sia il significato, che stia a “sinistra” di “Δ.

Se non si osserva la regola che le lettere minuscole dell’alfabeto, che abbiamo usato come simboli per generici ma determinati termini, debbano avere uno (e uno solo) significato (per cui di fatto sono “costanti”!) si potrà facilmente arrivare alle più assurde conclusioni come quelle già menzionate o di altro tipo; p.es. si potrebbe dedurre, dall’osservazione che il cane abbaia e che il cane è un sostantivo maschile, la verità (!?) che il sostantivo maschile debba necessariamente abbaiare!

Se vogliamo esplicitamente asserire che “a” rappresenta una proprietà scriveremno “a Î C”; dove ora “C”, al contrario di “a”, non è un simbolo arbitrario (nel qual caso avrebbe un significato variabile, nel particolare senso che il significato del simbolo varierebbe da una proposizione all’altra per cui bisognerà fissarlo di volta in volta in ogni singola proposizione). Invece “C” è un termine che ha sempre un significato costante nel senso che resterà invariato in tutto il nostro discorso.

Quindi intendererno sempre: “C = proprietà” (si può dire che “C” è il nome comune dei nomi comuni!). Allo stesso modo scriveremo “a Î I” se voglianmo dire che “a” rappresenta un individuo, quindi “I = individuo” .

Nella formalizzazione della logica pura (intendendo con tale locuzione l’insieme dei simboli, degli assiomi e dei teoremi pertinenti ad essa, con l’esclusione quindi della metalogica cioè del linguaggio con cui si parla di essa) non è necessario usare i termini “C” e “I”, bastando la convenzione metalinguistica che deriva dallo stare il simbolo a “destra” o a “sinistra” del segno “Δ, come già detto.

Nel caso che la logica venga usata come metalinguaggio per la costruzione di altri linguaggi scientifici (p.es., la matematica, nel qual caso le formule di logica funzioneranno da metamatematica) può risultare utile (anche se non necessario: infatti è sempre possibile introdurre apposite convenzioni nell’uso dei segni per evitarlo) menzionare l’ipotesi che un dato simbolo indichi una proprietà, scrivendo: “a ÎC” ; questo bisognerà farlo, in ogni caso, quando ci sia pericolo di ambiguità sul significato logico del simbolo “a”.

***

Faremo ancora finta di non sapere il significato della parola “proprietà” ma affermeremo che se “a” e “b” sono simboli che denotano proprietà, allora anche l’operazione:⁹ “” è una proprietà.

Questo è un esempio di quelle che si dicono definizioni ricorsive cioè: si elencano prima gli oggetti elementari che possiedono la proprietà da definire (in questo caso, le proprietà elementari sono rappresentate dai simboli semplici “a”, “b”) e poi si dà una regola per definire gli oggetti composti (nel nostro caso, le proprietà composte sono quelle del tipo “”). Con ciò ovviamente non si dà il significato reale del termine definito ricorsivamente (nel nostro caso, il termine proprietà), che invece dobbiamo già possedere, ma soltanto quello formale; quindi le definizioni ricorsive sono definizioni nominali anche se non ne hanno la forma esplicita che abbiamo descritto sopra.

Possiamo simbolizzare quanto detto con la formula:

(M1) ,

cioè

se “a” e “b” sono proprietà lo è anche “” e viceversa.

Dal punto di vista puramente formale non è necessario sapere il significato reale di “” (fermo restando il suo significato formale di operazione che date due proprietà ne produce una terza); ma se ne può dare una definizione reale (= descrizione) dicendo che “” significa la proprietà complementare della proprietà intersezione di “a” e “b”, cioè la proprietà di non essere “a” e “b” contemporaneamente.

In modo più formale: se qualcosa, p. es.: “x”, ha la proprietà “” allora necessariamente “x” non ha la proprietà intersezione di “a” e “b”, cioè o non ha la proprietà “a” o non ha la “b”; o, ancora, “x” non può essere “a” e “b” nello stesso tempo.

***

Per il significato che abbiamo dato al segno “ι”, possiamo convenire che “ιa” significa il “concetto” determinato completamente dalla proprietà “a”. Cioè: “ ιa .=. concetto di a”.

Notiamo che, dal momento che si ha sempre “a = a” e quindi “a Î ιa”, “a” ha la funzione di individuo nei confronti della proprietà “ιa”. In questa funzione diremo che “a” è l’“intensione” del concetto “ιa” o, che è lo stesso, “a” è l’intensione del concetto di “a”. Ma, naturalmente, la forma simbolica è più perspicua di qualunque adattamento, più o meno forzato, della lingua comune.

Nel caso che “a” sia un termine che rappresenti un individuo realmente (e non solo formalmente, cioè nel caso che il termine sia un nome proprio, come, p. es., Socrate) diremo che “a” è l’individuo e “ιa” è l’“idea” di “a” (Peano usava il nome elemento per essa, ma oggi tale nome viene usato come sinonimo di individuo).

Per esempio se uomo è una proprietà, ι uomo è il concetto di uomo. E uomo è l’intenzione del concetto di uomo. Se Socrate è un individuo ι Socrate è l’idea di Socrate.

Notiamo che “ι” si può considerare come un “operatore” che applicato ad un individuo ne produce la sua idea e applicato ad una proprietà ne produce il suo concetto.

Nell’ipotesi che, nel seguito, possa servire introdurremo l’“operatore inverso” di “ιa” che fa passare dal concetto alla sua intensione (o dall’idea all’individuo corrispondente). Lo indicheremo con “j”

Per esempio, se “b” è il concetto di uomo, “j b” è la proprietà uomo. Se “b” è l’idea di Socrate, “jb” è l’individuo Socrate.

Ne segue che: “j ιa = a” e “ι j a = a” qualunque cosa sia “a”.

Converremo, ancora, che se “a” è la proprietà che definisce il concetto “ι a” allora “áa” ne denota la sua “comprensione”.

Intenderemo, invece, con il termine “estensione” il gruppo di individui dei quali possiamo affermare che sono degli “a”; l’estensione di “ιa” differisce dall’intensione di “ιa” e la indicheremo, se dovesse servire, con “ext a”; ma vedremo che in un linguaggio scientifico tale segno non è necessario.¹⁰

Per le convenzioni fatte, le proposizioni elementari si possono tutte ricondurre alla forma “x Î a”, che all’occorrenza, abbrevieremo con il segno “a_x”, cioè:

(A4) a_x .=. x Î a

Per gli assiomi elencati in Appendice anche le proposizioni composte (cioè quelle formate analogamente alle proprietà composte) possono essere poste sotto tale forma. Per cui se conveniamo di abbreviare il termine proposizione con “P” possiamo scrivere:

(M2) x Î a . É . x Î I ∩ a Î C ∩ (x Î a) Î P,

cioè: la formula “x Î a” implica che “x” è un individuo, “a” è una proprietà e “x Î a” è una proposizione.

Notiamo che nella (A4), il segno “x Δ assume il ruolo di un “operatore” che, assegnato un determinato individuo “x”, ci fa passare da una data proprietà alla corrispondente proposizione relativa ad “x”.

In tale ruolo lo indicheremo con “Î_x”.

Possiamo, invece, assegnare al segno “'_x” il ruolo di “operatore inverso” che fa passare dalla proposizione relativa a “x” alla corrispettiva proprietà.

Per cui si avrà:

(A5) a_x .=. Î_x a ,

(A6) a .=. '_x a_x

Operando sui due membri delle due identità, rispettivamente, con “'_x” e “Î_x”, si ottiene:

'_x a_x = '_x Î_x a = a ,

Î_x a = Î_x '_x a_x = a_x ;

questo significa che i due operatori “'_x Î_x” e “Î_x '_x” operando, rispettivamente, su di una proprietà e su di una proposizione le lasciano inalterate; tale proprietà può risultare utile nelle deduzioni.

Infatti, lo scopo principale di un “sistema deduttivo” è quello di dedurre da proposizioni ritenute come vere altre proposizioni valide, in modo assolutamente meccanico mediante pochissime regole deduttive.

Le proposizioni che si assumono come vere si dicono “assiomi”, quelle dedotte dagli assiomi, mediante le regole deduttive, si dicono “teoremi”.

Tuttavia, è importante osservare che la distinzione tra termini primitivi e termini derivati, da un lato, e definizioni nominali, assiomi e teoremi dall’altro, ha un valore relativo e non assoluto. La scelta di cosa assumere come primitivo o come derivato è assolutamente arbitraria e dipende solo dalla volontà di chi costruisce il sistema deduttivo.

Tale scelta non dipende né da una necessità pratica, né teorica, ma solo da condizionamenti esterni dettati da valutazioni soggettive, quali: considerazioni estetiche, ricerca di semplicità, adeguamento a particolari concezioni del mondo o, anche e non ultime, ragioni economiche, ecc.

Per esempio, nell’industria dei calcolatori si sceglie (in questo caso, “fisicamente”, nel processo di produzione dei chip di silicio) l’operazione che abbiamo indicato con il simbolo “” (la chiameremo “operazione nand”, abbreviazione dell’inglese not and) come operazione primitiva, a partire dalla quale costruire le altre operazioni logiche, perché si riducono notevolmente i costi di produzione dei circuiti integrati.

La ricerca della “semplicità” è solo un mito, sia perché è un concetto difficile da definire, sia perchè una volta definitolo in un caso particolare non sarà più adatto in un altro caso.

Al contrario, il costo unitario di un determinato circuito integrato (e quindi il maggiore o minore profitto da ricavare dalla sua vendita), per il bene o per il male, è invece oggettivamente determinabile!

Il Peano, giustamente, non si preoccupa gran ché di stabilire un sistema assiomatizzato al massimo grado, convinto com’è che, in un linguaggio scientifico, da qualunque punto si parta, si debba necessariamente arrivare allo stesso risultato; purché non si scambino pseudoproblemi di natura puramente verbalistica per problemi effettivi che concernono i concetti e le idee (vedi comunque PF).

Tuttavia il suo collaboratore A. Padoa stabilisce un sistema deduttivo in cui, come termini primitivi di tutta la logica, si assumono solo tre termini; e precisamente quelli da noi indicati con “ =, ∩ e '_x”; a partire dai quali vengono definiti nominalmente tutti gli altri.¹¹

In generale, nei vari campi della scienza, non è nemmeno un’impresa semplice, ma, in qualche caso, richiede il lavoro di molti anni da parte di provetti matematici, il verificare se una data proposizione data come assioma non possa essere, invece, dimostrata come teorema a partire dagli altri assiomi.

In Appendice viene dato un possibile sistema di termini primitivi, di definizioni nominali e di assiomi per la logica.

Qui ci limiteremo a notare che a partire dall’operazione “~” si possono definire nominalmente tutti gli altri connettivi logici che servono a formare tutte le altre proprietà partendo da quelle elementari.

Per esempio la “proprietà complementare” di una data proprietà “a” si può definire mediante la:

(P1)

L’“unione” di due proprietà con:

(P2)

L’“intersezione” con

(P3)

Si è soliti sottindendere il segno di intersezione con la definizione:

(P4)

Con tale abbreviaziomie si realizza una consistenza simbolica con il segno originario “~”; infatti, operando sui due membri della (P4) con “~” si ottiene: “”.

Per realizzare un migliore aspetto tipografico delle formule useremo, talvolta, la convenzione di negare solo l’operazione invece che l’intera proposizione, p. es.: “” e “”.

Per la stessa ragione useremo, a volte, le convenzioni: “ ~ a . = . ~ (a) . = . ã ” .

Il significato reale dei segni introdotti mediante definizione nominale potrebbe desumersi a partire da quello dei segni primitivi.¹²

Possiamo asserire gli ovvi “assiomi” seguenti:

(P5)

cioè: facendo il complemento del complemento si riottiene la proprietà di partenza.

(P6)

che esprime la proprietà commutativa dell’operazione retta da “~”.

(P7) ,

con l’abreviazione:

(P8) .

Le (P7) e (P8) esprimono la proprietà associativa dell’operazione retta da “∩”.

(P9) ,

che esprime la proprietà distributiva di “∩” rispetto a “U” (il segno “∩”, per la convenzione (P4), è sottinteso nell’ultima formula).

(P10) ,

cioè: la proprietà “aã” è assurda. O, in altre parole, non è possibile che qualcosa sia “a” e “non-a” nello stesso tempo.¹³

Per le definizioni e gli assiomi dati, si possono assumere tre sole regole deduttive, che appelleremo:

D1. Regola di sostituzione tra simboli di segno uguale.

D2. Regola di sostituzione tra simboli di segno diverso.

La D1. ha origine dal significato del termine “simbolo” che, stando per un “generico” termine, permette di sostituire, in una data proposizione, un determinato simbolo con un qualsiasi altro simbolo; purché: a simboli di eguale nome si sostituiscano altri simboli che, corrispondentemente ed uniformemente, siano ancora di eguale nome; così, per esempio, la (P9) si può scrivere anche “x (y U z) . = . xy U xz” con identico significato. Ma non è lecita la sostituzione “x (y U z) . = . xb U xz” perché, se si cambia il nome di “b” con “y”, la sostituzione deve essere effettuata in tutti i posti in cui compaia il simbolo “b” nell’intera proposizione. Ciò in quanto, all’interno di ogni singola proposizione (o in una catena deduttiva), il simbolo ha significato “costante”, anche se è “variabile” da una proposizione all’altra.

La D2. ha origine dalla proprietà del segno “=”, che dà, identicamente, lo stesso significato ai termini a destra e a sinistra di esso. Seguendo il Padoa, la chiameremo: la proprietà sostitutiva del segno “=”. Infatti, se quello che sta a destra di “=” significa la stessa cosa di quello che sta a sinistra (e viceversa) ne segue che se si asserisce: “a = b”, si può sostituire “a” in qualunque formula compaia “b”, e viceversa. Per di più, qualunque operatore sia definito su “a”, lo si può applicare anche su “b” senza alterare l’identità.

Esprimendo quanto detto con una formula:

D3. Se “ω” è un operatore che ha senso applicare al termine simbolizzato da “x” allora:

x = y . É . ω x = ω y ,

anzi, se “ω” ammette un inverso allora il segno “É” si può sostituire nell’ultima formula con il segno “=”.

Per la proprietà sostitutiva del segno “=” non è necessario, per questa seconda regola deduttiva, operare la sostituzione del simbolo in tutti i posti in cui esso compaia, dato che il simbolo che si va a sostituire ha lo stesso significato di quello che lo sostituisce (infatti sono sinonimi). Solo ragioni di convenienza, a fini deduttivi, ci suggeriscono dove e quando operare la sostituzione.

Dalla proprietà sostitutiva del segno “=” vengono fuori immediatamente le proprietà caratteristiche dell’identità e cioè le proprietà: riflessiva, simmetrica e transitiva. E cioè:

(I1) a = a

(I2) a = b . = . b = a

(I3) (a = b) ∩ (b = c) . = . (a = c)

***

A partire dalle (P1) - (P10), mediante le regole deduttive D1., D2., D3., si possono dedurre molti teoremi sulle proprietà.¹⁴

Se si introduce l’assioma:

(P11) a É b . = . ab = a ,

la comprensione di un concetto diventa una struttura ordinata dalla relazione “É”.¹⁵

Una struttura analoga si verrà a generare anche per le proposizioni, a partire dall’assioma del metalinguaggio (analogo di M1):

(M3) ,

se si assumono assiomi analoghi ai (P1) - (P10) (vedi Appendice).

Qui notiamo solo che, ovviamente, l’operazione di complementazione diventa la “negazione”.

L’unione diventa la “disgiunzione inclusiva”.

L’intersezione diventa la “congiunzione”.

L’assioma (P5) diventa l’asserzione metalinguistica che “due negazioni affermano”.

Valgono, analogamente, le proprietà: commutativa, associativa e distributiva.

L’inclusione tra proprietà diventa l’“implicazione” tra proposizioni (detta anche segno di “deduzione”).

Anche qui vale il fortissimo assioma:¹⁶

(Q11) a_x É b_y . = . a_xb_y = a_x .

Nel caso che tutte le proposizioni si riferiscano ad un solo individuo “x”, si instaura un perfetto isomorfismo tra le due strutture formali relative alle proprietà e alle corrispettive proposizioni riguardanti il detto individuo; ciò si ottiene formalmente con l’assioma:

(C1) (ab)_x . = . a_xb_x .

Un altro importante assioma e:

(C2) xÎa . = . ι x Î áa . = . i x É a

che permette di dimostrare un’altra forma di sillogismo relativo alle asserzioni singolari:

(C3) a_x ∩ (a É b) . É . b_x .

Un altro ovvio assioma, che come il (C2) permette il collegamento tra proprietà di un livello a quelle di livello superiore, è:

(C4) a Î áb . = . áa Î ááb

che, ovviamente, si può scrivere anche:

(C4’) a É b . = . áa É áb

Parentesi epistemologica

Fin dal tempo in cui l’uomo ha cominciato a riflettere su se stesso e sulla realtà che lo circonda, egli ha coltivato due superbe illusioni; da un lato, quella di scrivere un libro, simile a quello delle fantastiche invenzioni di Borges, in cui vi fossero elencate tutte le proposizioni della conoscenza universale ricavate da un’infinita sequenza di osservazioni empiriche. Questo, e solo questo, avrebbe costituito «LA SCIENZA» e, per sapere qualsiasi cosa relativa all’universo fisico e mentale, sarebbe bastato consultare questo immenso vocabolario, dovendosi solo conoscere l’ordine in cui le conoscenze furono disposte.

Da questa illusione, nasce l’idea dell’“uomo dotto” come magazzino di informazioni varie, benché sconnesse, che ancora dura ai nostri giorni e, anzi, si rafforza per via dell’infinita congerie di informazioni su presunti risultati di scienze confuse, diffuse, profuse dagli odierni mezzi di informazione di massa.

Dalla stessa illusione nascono le innumerevoli filosofie che, sotto diversi nomi, si rifanno alla concezione empirista della realtà.

Ma, non appena si cominci a stendere tale libro, anche nelle dimensioni le più ridotte, ci si accorge subito che non è per nulla facile trovare l’ordinamento più razionale affinché esso risulti di facile consultazione. Si scopre che è indispensabile un criterio di classificazione.

Nasce così la tassonomia e le sue strutture astratte che, ora, vengono identificate con “LA SCIENZA”.

Ciò, a un certo punto, crea la seconda superba illusione, secondo la quale, un bel giorno, l’uomo sarà in grado di possedere un’unica e breve formula magica a partire dalla quale, senza nemmeno più consultare il risultato degli esperimenti, si potranno dedurre tutte le conoscenze dell’universo. Questo crea il mito dell’“uomo colto” che, seduto a tavolino con la pipa in bocca, alla stregua di Ercole Poirot, da pochi indizi ricrea presente, passato e futuro.

La stessa illusione dà origine alle pratiche magiche ed a tutte quelle filosofie che sotto vari nomi si rifanno alla concezione idealista della realtà.

Si potrebbe pensare che chi coltiva la prima illusione non possa coltivare la seconda e viceversa. Ma ciò non è vero perchè l’una illusione è conseguenza dell’altra, come appunto gli empiristi logici stanno a dimostrare, non solamente, guardando al nome con cui si qualificano!

Ora ci occuperemo un momento degli effetti della cattiva filosofia di cui alla citazione di Engels in nota⁸.

Quando ci si voglia occupare scientificamente di un determinato campo di ricerca bisogna necessariamente delimitarlo.

Gli epistemologi di orientamento empirista pensano che, intanto, bisogna partire dai fatti, cioè dal dato empirico. Altri obbiettano che ciò è praticamente impossibile dal momento che in nessuna scienza esiste il dato empirico in astratto ma solo una ben particolare selezione di dati. E per fare tale selezione preventiva noi dobbiamo essere già in possesso di una teoria anche se in una forma ancora rudimentale.

La più rozza forma di teoria deve partire da alcune proprietà che, all’inizio, saranno necessariamente vaghe e non ben definite ma che possono permettere una prima classificazione. Qui siamo ancora in una fase puramente tassonomica o, per usare la terminologia di Bunge,¹⁷ in una fase protoscientifica.

Dal momento che ciò sembra ovvio e banale c’è da chiedersi come mai gli empiristi trascurano questo “fatto”, visto che si appellano ai “fatti”.

Inseguendo le loro argomentazioni ci si accorge che essi usano il termine fatto nell’accezione della lingua comune, la quale porta a confondere gli elementi teorici con gli elementi fattuali.

Il sostantivo fatto è omonimo del participio passato del verbo fare. Ma, nell’accezione comune, il sostantivo, da tale participio derivato, assume i significati relativi a tutti i tempi del participio: presente, passato e futuro.

Per cui, usualmente, molti considerano un fatto il contenuto semantico della proposizione: chiunque cada dalla finestra finisce a terra.

È ovvio che questa non si riferisce al passato, come in sono caduto dalla finestra e sono finito a terra che, effettivamente, si riferisce ad un “fatto”; ma, piuttosto, rappresenta un futuro ipotetico ed ha la struttura di una legge fisica che, in ogni caso, contiene elementi teorici e, come minimo, presuppone il postulato metafisico induttivista che se una correlazione tra due fatti si è sempre verificata in passato deve continuare a verificarsi in futuro.

Intanto, la proposizione precedente si deve, correttamente, porre nella forma se qualcuno cade dalla finestra, allora egli finisce a terra ovvero x Î a É x Î b, dove “x” è il qualcuno, “a” è la proprietà di cadere dalla finestra e “b” quella di finire a terra.

Più semplicemente possiamo scrivere a É b, dal momento che, in ogni discorso teorico si fa l’ipotesi forte che la legge vale qualunque sia l’individuo “x”, per cui la proprietà coincide con la sua estensione, ipotesi questa che dovrà mantenersi fino a prova contraria, altrimenti sarebbe difficile fare qualsiasi deduzione che non sia banale.

Per la fisica, la precedente proposizione è vera ma è ellittica e la si dovrebbe completare con un sistema deduttivo di proposizioni del tipo:

1) Tutti i corpi soggetti alla forza di gravità sono accelerati lungo la direzione della forza stessa.

Questo è un principio fisico che, nella teoria, assume il ruolo di assioma; il che è un modo per dire che è una proposizione primitiva, cioè indimostrabile (e nemmeno verifìcabile, visto che noi possiamo sperimentare solo sotto certe particolari condizioni mentre il principio è espresso in forma universale).

2) Sulla terra c’è un campo di forze di gravità diretto dall’alto verso il basso.

Anche questo è un assioma.

3) x è soggetto alla forza di gravità della terra ed è libero di cadere perché la finestra è situata in alto rispetto alla superficie della terra.

Questa è una condizione iniziale. Nella teoria assume il ruolo di ipotesi, eventualmente da verificare empiricamente, da assumere anch’essa come proposizione primitiva.

4) x finisce a terra per 1), 2), 3) e per le leggi del movimento.

Risultato verificabile empiricamente. Nella teoria è un teorema.

Ma questa è solo una rozza semplificazione che serve solo a dare l’idea della complessità di una descrizione scientifica del fenomeno considerato.

A questo punto qualcuno potrebbe pensare che la descrizione scientifica complica inutilmente le cose solo per dire, né più né meno, quello che, non solo già sapevano, ma che, addirittura era assolutamente necessario sapere per avere una pur minima legittimità nell’asserire i princìpi fisici da cui si tira la conclusione.

Ciò è tremendamente vero!

Ma la spiegazione scientifica non ha lo scopo di dedurre cose banali da cose banali (come spesso appare dopo avere letto i più famosi libri di epistemologia!). Ma il suo scopo è quello di dedurre, rigorosamente, da cose assolutanmemìte banali, o ritenute tali, cose di gran lunga più complicate come, p. es., dedurre l’istante preciso in cui un missile (lanciato dalla terra da un certo posto e in un certo istante) raggiungerà il pianeta Marte ed in quale preciso punto.

La previsione risulterà più interessante se quello che si deduce è paradossale, perché questo imporrà la scelta tra le ipotesi di partenza e le conclusioni finali o, quanto meno, una reinterpretazione della teoria; non potendosi, almeno logicamente, mantenere due proposizioni contradittorie.

E qui si capisce a che serve la logica!

Essa non ci può dire niente sulla verità delle ipotesi e degli assiomi, né su quella delle conclusioni!

Ma ci può dire se ipotesi, assiomi e conclusioni siano contradittori o compatibili. E ciò è molto importante per la scienza.

La logica non è la scienza della VERITÀ ma, semplicemente, un piccolo insieme di regole di deduzione. Anzi, non è nemmeno una scienza ma una precondizione di ogni scienza!

Allora, come già sapevano gli antichi, nella scienza non si parte dai fatti ma dalle proprietà, (o dai concetti che è lo stesso) che una volta astratte dall’esperienza sono gli individui della nostra comprensione e gli elementi della nostra teoria.

La comprensione è un insieme strutturato di proprietà; è un’algebra di Boole, come già detto nella sezione precedente.

Quanto detto vale anche per una scienza puramente empirica, cioè priva di qualunque forma di teoria la quale possa assumere “a priori” i suoi elementi costitutivi.

Infatti, per la costituzione di un linguaggio scientifico si parte (consciamente o inconsciamente) da un insieme non strutturato di proprietà, che chiameremo i generatori dell’algebra (sottinderemo: della comprensione); essa delimita il campo di ricerca.

Tutte le altre proprietà del campo di ricerca, elementi compresi, possono essere generate, appunto, da tali generatori mediante l’operazione tra proprietà, nand, che abbiamo indicato con il simbolo .

Potrebbe sembrare, a prima vista, che partendo da un numero finito di proprietà si possa generare tutta un’infinità di altre proprietà, per effetto di successive e ripetute applicazioni dell’operazione nand.

Ma ciò non è vero, in quanto gli assiomi che sono stati dati nella sezione precedente limitano enormemente il numero delle proprietà semanticamente differenti. Si dimostra, infatti, che se si parte da n generatori si possono ottenere solo N £ 2ⁿ proprietà atomiche, cioè proprietà, mutuamente incompatibili, mediante le quali si può generare tutta l’algebra della comprensione, che conterrà esattamente 2^N proprietà, comprese la proprietà assurda, che abbiamo indicato con , e la sua complementare, che indicheremo con e che chiameremo la “proprietà banale”, cioè quella proprietà posseduta da tutti gli individui che costituiscono il campo di ricerca.

Faremo il postulato che le proprietà della comprensione, così generata, costituiscano tutte e sole le proprietà possedute dagli individui del campo di ricerca.

Tra le proprietà generate, alcune hanno un’importanza maggiore delle altre; per cui risulta utile introdurre, mediante definizione nominale, dei segni particolari per esse.

Il massimo numero di proprietà atomiche, N = 2ⁿ, si otterrà solo quando capiti che si siano scelti i generatori tutti indipendenti tra loro di modo che, presi due qualunque di essi, p.es. “a” e “b”, si abbiano certamente individui che posseggono contemporaneamente entrambe le proprietà, cioè, quando si possa certamente asserire: $ ab.

Ne segue che, se con Aristotele, pensassimo di definire la sostanza o essenza (ούσία) come la proprietà dell’esistenza delle cose (facendo astrazione da ogni altra proprietà), si avrebbe n = 0, N = 2⁰ = 1 e la comprensione avrebbe solo 2^N= 2¹ = 2 proprietà e cioè solo la proprietà assurda e la proprietà banale, come Parmenide cercava di far capire agli empiristi che precedettero l’empirista Aristotele. Ma ciò lo esamineremo più dettagliatamente in seguito.

***

Ma, per potere entrare nei dettagli della scienza degli antichi, è necessario chiarire alcune questioni metodologiche.

Solo pochissimi frammenti ci sono pervenuti dei cosiddetti presocratici.

Quasi tutto quello che sappiamo, o che crediamo di sapere, ci proviene dai dossografi.

Si potrebbe pensare che con un minuzioso lavoro filologico si possa ricostruire, in qualche modo, il loro pensiero. Questa, in ogni caso, è l’opinione generale. Ma noi pensiamo che la filologia non è di nessuno aiuto in questa impresa. La riprova di ciò è che ci sono tanti Parmenidi e tanti Democriti per quanti filologi ci siano.

Escludiamo, ovviamente, dal novero dei filologi tutti quelli che hanno seguito (o che seguono) un ben determinato paradigma. Ché, per i ben noti meccanismi della carriera accademica, non aggiungono niente di nuovo.

È per la forza del paradigma aristotelico che molti dossografi sembrano dire la stessa cosa. Di fatto, non fanno altro, per lo più, che pestare e ripestare le opinioni di Aristotele, con la convinzione, che ancora perdura, che il pensiero di Aristotele, ritenuto il più grande scienziato del passato, fosse più maturo dei suoi predecessori. Questo in omaggio a quella che abbiamo chiamato la teoria delle PULCI.

Se si abbandona questa teoria si potrebbe pervenire alla conclusione che Aristotele rappresenta un profondo arretramento nel processo di costruzione del linguaggio scientifico.

Ma se neghiamo valore ai dossografi e al loro progenitore Aristotele come potremo procedere?

Semplicemente sostituendo la logica (come chiarita da Peano) alle speculazioni metafisiche che cercano supporto nella filologia.

Già lo stesso Peano aveva ricostruito, con i suoi “simboli”, l’opera di Euclide; nella convinzione (che è anche la nostra) che, da qualunque punto si parta, se si procede coerentemente e senza ambiguità, il risultato deve necessariamente essere lo stesso, se le ipotesi di partenza sono le stesse.

Ma quali erano le ipotesi dei “presocratici”?

Questo ce lo faremo dire dallo stesso Aristotele, che nel criticarli, le ha enunziate, anche se malamente illuminate, all’ombra del suo paradigma.

Quindi per studiare i presocratici saremo costretti a partire da Aristotele; ma non dalle sue conclusioni, bensì da un’analisi logica del suo paradigma.

***

Accettando le conclusioni di Max Müller,¹⁸ Peano notava che le categorie grammaticali derivano da Aristotele, il quale elenca dieci categorie logiche in corrispondenza con le parti del discorso della grammatica greca. Lo stesso Müller osservava che la classificazione dei vocaboli nella lingua semita e in quella cinese era ben diversa.

Questo significava, per Peano, che altro sono le proprietà reali dei nomi e altra cosa le proprietà formali, in quanto derivanti esclusivamente dalla tradizione linguistica.¹⁹

A partire da questo possiamo concludere alcune cose ovvie.

Si dice spesso che Aristotele è da considerare il padre della logica. Peano, in più di un’occasione, nota che la logica di Aristotele è di nessun uso per la matematica. La diversità concettuale, del resto, salta immediatamente agli occhi.

D’altra parte, le conquiste nel campo della matematica dei presocratici sono immense. Si pensi ad Eudosso e Democrito che godevano la profonda ammirazione di Archimede.²⁰

Ovviamente, non si può fare matematica senza logica; e, del resto, tra le opere di Democrito, elencate da Diogene Laerzio tra gli scritti di fisica, vi figura Logica o Canone in tre libri.²¹

Se ne può semplicemente concludere che la logica di Aristotele è la logica del senso comune e quella di Democrito doveva necessariamente essere quella della matematica.

***

Quale dovrebbe essere la logica della scienza in generale?

Per Democrito non ci sarebbe potuto essere alcun dubbio, visto che per lui la scienza era una e non era divisa in branche e sottobranche di specialisti che, secondo l’aforisma di Bernard Show, sono coloro che sanno tutto su nulla.

Oggi, la risposta non sembra così ovvia, anche a causa della confusione epistemologica di marca russelliana, ancora imperante! (si veda PF).

È utile entrare, per un momento, in qualche dettaglio per capire la profonda differenza tra le metafisiche che si nascondono sotto dei simboli apparentemente uguali e per vedere come lo scontro tra queste due contrapposte metafisiche non è diverso da quello che ciclicamente si è verificato nel corso della storia.

Come viene chiarito in PF, tale differenza si manifesta nell’interpretazione estensionale del termine classe nell’una concezione del mondo contrapposta a quella intensionale dell’altra.

Al senso comune appare che gli oggetti immediati della nostra percezione siano le “cose” in quanto “individui”. Da esse noi formeremmo gli aggregati di cose. Successivamente, avendo dato un nome all’aggregato, raggiungeremmo la “classe”.

Se così fosse non avremmo nemmeno bisogno di nominare le proprietà.

Infatti nella logica empirista il ruolo delle classi risulta del tutto marginale ed il ruolo primario viene assunto dalle proposizioni categoriche.

Per esempio, Russell (vedi PF) concede qualche ruolo alle intensioni solo per parlare dei numeri transfiniti, che per altro, nessuna applicazione trovano nelle scienze.

Saltando, così, con un solo incredibile balzo, dalle banalità della logica del senso comune agli iperuranici meandri dell’infinito.

Tuttavia, una tale filosofia ha un profondo fascino; perchè conforta gli sciocchi che si sentono a loro agio nel linguaggio atavicamente acquisito e pretendono di stupire il mondo con i supposti paradossi della matematica. Allo stesso modo di Aristotele che pretendeva di superare quelle che egli chiamava le aporie di Zenone; le quali, invece, come vedremo, erano dei semplici teoremi. Il paradosso nasceva solo al confronto con le difettose premesse aristoteliche.

Uno potrebbe, ingenuamente, pensare che, quando si incontrano dei paradossi, vuol dire che i significati degli assiomi di partenza (essendo libere creazioni dell’intelletto umano!) siano contraddittori; ma i falsi profeti concludono diversamente; ipotizzando, inconsciamente o esplicitamente, che i loro assiomi e relativi significati siano leggi imposteci dalla natura; per cui bisogna abituarsi a convivere con paradossi ed aporie, cercando di arrangiarsi a fare il meglio che si può acciocché non diano soverchio fastidio quando dal mondo iperuraneo del pensiero astratto si voglia fare il tentativo di applicarle a situazioni concrete o pseudoconcrete.

Per assaporarne, in seguito, le analogie coi discorsi degli antichi, esaminiamo il paradosso centrale dei logici moderni che è, appunto, quello che va sotto il nome di “paradosso di Russell” e che deriva, sostanzialmente (senza tenere conto delle infinite chiacchiere inutili) dal dogma che la matematica si occupa solo di estensioni e dalla conseguente identificazione del termine classe con il termine aggregato. (Per capire come Russell doveva, necessarianmente, arrivare al paradosso basta leggere la confusa ed incomprensibile distinzione tra classe, concetto e concetto-classe nell’intero capitolo dedicato a tale questione nel suo The principles of mathematics, dove con argomenti non dissimili da quelli medioevali, riferentisi al sesso degli angeli, si critica, anche a sproposito, la chiara e precisa impostazione di Peano; vedi, comunque, PF).

Per Peano, al contrario, la logica non è una scienza a sé sulla quale esercitarsi con l’alta matematica, per poi applicarla ad astruse questioni metafisiche (nel senso deteriore di tale termine) ma è un semplice strumento per il chiarimento dei concetti della matematica; la quale, a sua volta, non serve per costruire castelli di carta della più inutile astrazione, ma costruisce le sue strutture formali a partire da modelli che idealizzano le concrete operazioni della scienza empirica.²²

Per Russell, la matematica è quella scienza che non deve sapere nemmeno di che cosa tratta, secondo un paradossale aforisma russelliano. Ma nonostante ciò, egli procede impunemente a matematizzare la logica.

L’obiezione, più ovvia, a una tale impostazione è quella di notare, banalmente, che fare della matematica sulla logica che, a sua volta, deve servire a fondare la matematica, equivale a porsi l’irresolubile problema di sapere se è nato prima l’uovo o la gallina; come tutte le successive chiacchiere inutili sul sovrumano problema dei fondamenti della matematica stanno a dimostrare. Infatti, la conclusione a cui giungono i superlogici che si autodefiniscono metamatematici è la contradittoria asserzione che, da un lato, la matematica non si può fondare sulla logica (vedi le varie interpretazioni del famigerato teorema di Goedel) e che, d’altro lato, la matematica è riducibile ai concetti della logica.

Ma vediamo di capire l’essenza del tremendo ed esiziale paradosso di Russell.

Se, come abbiamo convenuto, scriviamo “a e C” per dire che “a” è una classe, dove “a” e un simbolo che può assumere qualunque valore semantico (ovviamente tra i termini che denotano una classe), possiamo pensare di essere liberi di attribuire ad “a” il particolare valore “C”, scrivendo “CÎC”.

Se interpretiamo “C” come sinonimo di mucchio, cioè estensionalmente, e, ancora arbitrariamente, ipotizziamo di essere liberi di creare astrattamente dei mucchi con la sola potenza del nostro pensiero, possiamo pensare, che oltre a “C”, ci siano altri mucchi per i quali si possa scrivere “a Î a” (pressappoco come quel fantastico mucchio di spaghetti che contiene la pentola che li contiene; infatti basterà ribattezzare la pentola con il più pomposo nome di insieme degli spaghetti che contiene se stesso!) chiamiamo tali chimerici mucchi:

insiemi chiusi.

Ovviamente ci sono anche banalissimi insiemi che fra i loro membri non contengono lo stesso insieme che li deve contenere, chiamiamoli: insiemi aperti.

Immaginiamo ora, sempre con l’infinita potenza del nostro pensiero, di compiere un ultimo atto di creazione e generiamo Eva dalla costola di Adamo inventandoci l’insieme di tutti gli insiemi aperti che chiameremo “R”.

Nasce un tremendo problema che assomiglia al problema di Wiener il quale si chiede se, essendo Dio onnipotente, possa creare un masso così pesante, ma così pesante, che Egli stesso non possa sollevare. Il problema o non ha soluzione perché mal posto o conduce ad una contraddizione che viene a negare l’onnipotenza di Dio. Infatti o è in grado di creare il masso e allora non potrà sollevarlo o non ne sarà in grado. In ogni caso, non sarebbe onnipotente.

Non dissimile il problema di Russell: è R chiuso o aperto?!

Se è chiuso dovrà aversi R Î R. Ma R era l’insieme degli aperti e, quindi, R Ï R, per definizione.

Se è aperto dovrà aversi R Ï R ma allora dal momemmto che R è aperto dovrà essere contenuto in R che è l’insieme degli aperti e quindi R Î R.

Allora, o la questione è mal posta o il pensiero astratto non è onnipotente. Noi pensiamo che entrambe le ipotesi siano vere!

Ma forse che, da questa patente contraddizione, Russell ed i “logici” posteriori concludono che ci deve essere qualcosa di marcio sotto? No!, al contrario, pensano che sia un brutto scherzo della natura stessa della logica e quindi ricorrono a delle pezze per salvare il salvabile e, così Russell si inventa la famigerata ed inutilmente complessa teoria dei tipi che complicherebbe enormemente la vita ai matematici che, infatti, l’hanno sempre rifiutata.

Tuttavia, questi ultimni o fanno limita di niente, forse tacitamente assumendo che la questione è malposta, o ricorrono ad una semanticamente non chiarita distinzione tra insieme e classe aggiungendo un, praticamente inutile, postulato secondo il quale, affinché qualcosa sia un insieme non basta che ci siano degli individui che vi appartengano ma deve esistere, anche, un non meglio specificato ente a cui l’insieme stesso deve appartenere; con divertenti conseguenze quando le astratte formule si volessero interpretare semanticamente.

Infatti, a causa dello stesso errore che porta ai paradossi, Whitehead e Russell, insieme ad altri posteriori assiomatizzatori, giungono a definire l’insieme vuoto come l’insieme di quegli individui per cui valga la proposizione “x ¹ x” e la classe universale viene definita come la classe di quegli individui per cui valga la proposizione “x = x”.

Analizzando le precedenti definizioni con l’ideografia di Peano se ne può misurare facilmente la loro assurdità.

Per quanto riguarda la classe universale: usando il precedentemente introdotto simbolo per la formazione di classi a partire dalle proposizioni, si ha “'_x (x = x)” e per la decomposizione di “ = ” : “'_x Î_x ι x” che, per la proprietà già menzionata dell’operatore '_x Î_x , si riduce semplicemente a “ι x”. Per cui la classe universale si riduce a quella che abbiamo chiamato l’idea di “ x” che, in ogni caso, è una classe con un solo individuo.

Ma, essendo “ x” un simbolo generico senza significato definito, si conclude che la classe universale è la proprietà di nessun individuo determinato e quindi la proprietà assurda.

Allo stesso modo, per l’insieme vuoto si ha: “'_x (x ¹ x)” e quindi “'_x Î_x ~ ι x” e, alla fine, ~ ι x ; in conclusione: la proprietà complementare delle cose che non hanno significato e quindi, se volessimo insistere sull’interpretazione estensionale, la proprietà di tutte le cose che significano qualcosa; per cui l’insieme “vuoto” viene ad essere “pieno” zeppo!

E si potrebbe continuare, con divertimento, a volontà!

Nella formulazione di Peano, tali assurdità non possono mai presentarsi; infatti: non ha senso scrivere “ x Î x” (come in molte altre rinomate assiomatizzazioni si scrive!) ma solo “ x Î áx” o “ x Î ι x” qualunque cosa sia “x”, in particolare anche “C”.

Per cui, al massimo, potremmo ottenere solo le banali asserzioni “C É C” o “C = C” che sono, ovviamente, sempre vere e ci dicono: nel primo caso che la classe è una sottoclasse del termine classe o, in altre parole, che il termine classe è un membro della comprensione del concetto di classe; come, d’altra parte, vale per qualsiasi altro termine!

Nel secondo caso avremo che la classe è identica alla classe o, in altre, parole che il termine classe è un membro del concetto di classe.

Tutte queste frasi sono modi più precisi, anche se inutili e banali, di enunciare l’ambigua affermazione del linguaggio comune che una classe è una classe!

Come sempre, i paradossi derivano da una ben povera teoria! Ma la gente sembra deliziarsi con i paradossi e ne va costantemente alla ricerca in ogni campo della SCIENZA (naturalmente di quella scritta a caratteri maiuscoli!).

***

La confusione epistemologica, a nostro giudizio, può essere portata avanti solo per un profondo malinteso sul ruolo della matematica nella scienza.

C’è, intanto, un’importante distinzione che bisogna fare entro le scienze particolari a cui la logica si applica, distinguendo tra quelle formali, come la matematica, quando si astrae da qualunque applicazione concreta, e quelle empiriche in cui la matematica è nient’altro che il mezzo per organizzare ogni discorso.

Nel primo caso si ha solamente una struttura formale non interpretata. Nel secondo caso, oltre alla prima, che spesso si dice la teoria, si ha anche tutta una serie di affermazioni riguardanti i dati empirici, cioè esperimenti, osservazioni empiriche, e loro risultati fattuali, i cui termini sono dotati di significato non formale, ma operazionale.

Il collegamento tra le due parti del linguaggio viene operato mediante un processo di interpretazione di natura solamente e, necessariamente, metafisica (cioè non dimostrabile formalmente, nè verificabile empiricamente) che consiste nello stabilire opportune relazioni tra termini definiti operazionalmente e termimui definiti teoricamente.

Solo allora i teoremi dedotti dalle ipotesi teoriche potranno essere falsificati empiricamente se, per di più, si stabilisce un limite di accettabilità, tenuto conto che, in ogni esperimento reale, siamo costretti a un processo di idealizzazione per cui, solo statisticamente, si possono trarne conclusioni intorno all’accordo tra teoria ed esperimento.²³

Gli stessi termini operazionalmente definiti presuppongono elementi teorici, anche se non formalizzati, provenienti dal, generalmente inconscio, processo di concretizzazione o ipostatizzazione degli enti astratti (cioè che sono stati “astratti” dal caotico mondo delle sensazioni).

A maggior ragione, gli assiomi della teoria (che, ovviamente, non sono direttamente collegati ai termini del linguaggio empirico) sono astrazioni; ma, in questo caso, è più opportuno dire idealizzazioni, intendendo con quest’ultimo termine il processo per cui, da determinate proprietà precedentemente astratte dal mondo sensibile (anche se nei contesti i più disparati), a partire dalla ripetuta applicazione dell’operazione tra proprietà che abbiamo indicato con , si generano altre proprietà che definiscono una nuova idea generale, che non fa parte delle cose osservabili.

Un esempio si ha in meccanica classica dove si definisce il concetto di punto materiale, mediante le proprietà astratte di essere senza dimensioni fisiche e, tuttavia, dotato di massa. Dopodichè si attribuisce agli individui di tale classe astratta anche la proprietà dell’esistenza; quindi concretizzandola.²⁴

Dal momento che i termini della teoria rappresentano idealizzazioni e che, quindi, gli individui sono definiti a partire dalle proprietà, e non viceversa (anche gli enti, cosiddetti, sensibili sono, anche se spesso inconsciamente, definiti per proprietà!), ne consegue che tali termini, per parlare propriamente, non avrebbero un’estensione, se volessimo usare tale termine nell’accezione degli empinisti, nella quale si mantiene l’illusione che vi siano oggetti che “esistono” in quanto sensorialmente percepiti. Quando invece in realtà si assume ipostaticamente che esistono realmente proprio perché creati indipendentemente dai nostri sensi e cioè al di là del caos sensoriale.

Ragione per cui, nel linguaggio teorico, assumiamo (o, facciamo la convenzione, come dice Peano) che l’estensione coincida con l’intensione. Per cui la classe si può far coincidere con la proprietà che la definisce.

Ma se tale identificazione, tra intensione ed estensione, va bene nel linguaggio teorico di una scienza empirica, non va per niente bene in un linguaggio puramente tassonomico.

Infatti, senza la convenzione “ext a = a”, possiamo solo scrivere: “a É ext a” (ma non viceversa) e non saremmo più autorizzati a generare tutta l’algebra della comprensione e, al massimo, potremmo pervenire a una struttura formale meno forte (esattamente si perverrebbe a quello che i matematici chiamano un reticolo non distributivo).

Per vederne la ragione, esaminiamo la scoperta già attribuita ai Pitagorici (PR p. 131)²⁵ che la stella del mattino e la stella della sera sono termini diversi per lo stesso oggetto.

Le proprietà che i due termini descrivono sono diverse e non può sussistere nessuna relazione di inclusione tra di esse.

Empiricamente niente potremo dire su una loro eventuale relazione; al massimo potremmo osservare determinate correlazioni tra certe particolari osservazioni.

L’asserzione della loro equivalenza estensionale può derivare solo da una teoria fisica sulla costituzione del sistema solare che creerebbe un altro concetto (di ancora diversa intensione): il pianeta Venere.

A questo punto, non saremmo in grado di stabilire nessuna relazione di inclusione tra le tre proprietà diverse. Avremo bisogno di tutta una, piuttosto complessa, teoria che leghi il moto dei pianeti alle nostre osservazioni empiriche; e, quindi (come minimo) di una qualche teoria della luce.

L’algebra di Boole di questo sistema teorico sarebbe davvero troppo vasta. Ma senza di questa non potremmo scrivere nessuna relazione logica fra le tre proprietà.

Ma, naturalmente, la scienza teorica procede per altre vie. Cioè introducendo altre relazioni oltre a quelle puramente logiche e che, invece, sono specifiche delle varie scienze particolari (mediante le cosiddette definizioni per astrazione — vedi PF).

Da ciò risulta chiaro che il mito empirista è assolutamente vacuo.

Così come lo è quello del razionalismo estremo; il quale viene derivato dal primo mediante l’illusione di poter trovare una regoletta universale che spiega tutto anche a costo di partire da strutture meno forti (come in meccanica quantistica) dell’algebra della comprensione e che si limitino a rispondere solo sul risultato di possibili misure.

Da questa osservazione, la fisica moderna, dentro il paradigma della meccanica quantistica, conclude che bisogna rinunciare a costruire l’algebra di Boole, accontentandosi di un reticolo non distributivo; al quale, arbitrariamente, si attribuisce la proprietà di modularità debole. Ciò semplicemente allo scopo di salvare il mito empirista.

Ma se si rinuncia alla SCIENZA UNIVERSALE, si possono ben spiegare le nostre osservazioni empiriche con “modelli” parziali nell’estensione ma strutturalmente completi.

Solo allora è possibile e, anzi, necessario identificare l’intensione di un concetto con la sua estensione, se si vuole “dedurre” qualcosa.

Ma ciò, certamente, non potrà essere possibile nella matematica, quando la si voglia considerare come un puro gioco astratto di simboli, nel qual caso, parlare di estensione non avrebbe molto senso, potendosi essa riformulare in modo da non nominare assolutamente gli individui.

Ma, piuttosto, nella “teoria” delle scienze empiriche.

Vedremo che questa era la filosofia degli antichi scienziati che vengono qualificati come Italici.

Il linguaggio scientifico dei preso cratici.

Essere e Non-essere.

L’intreccio tra le due contrastanti metafisiche di cui alla sezione precedente è molto antico.

P.es., Diogene Laerzio nel Proemio alle sue Vite dei Filosofi divide i filosofi antichi in due principali tradizioni: la Ionica che fa capo a Talete e l’Italica originatasi da Pitagora.

Non sembra che il criterio di classificazione di Diogeime fosse geografico in quanto molti tra gli Ionici non erano della Ionia, nè tutti gli Italici erano dell’Italia. Tale ripartizione è molto antica e si fa risalire a Sozione.

Infatti tra gli Ionici oltre, ovviamente, a Talete, Anassimandro, Anassimene e Anassagora, vengono annoverati anche Socrate, Platone e Aristotele. E tra gli Italici troviamo oltre a Pitagora, Empedocle, Archita, Filolao, Parmenide e Zenone, anche Eudosso, Senofane, Leucippo, Democrito, Protagora ed Epicuro.

È probabile che la bipartizione avesse a che fare, invece, con il differente dogma centrale che ognuna delle due tradizioni assumeva. Esso si riferiva alle due possibili alternative per l’interpretazione del termine realtà.

Nella tradizione ionica la realtà inizialmente viene, sostanzialmente, identificata con il dato dei sensi; la conoscenza della realtà quindi è data immediatamente e la ragione umana può solo limitarsi a classificare le sue esperienze, la matematica non è adatta per la comprensione della complessità del reale come concluderà Aristotele (Metaf. 995a 15-20): “Nè, d’altra parte, si deve pretendere l’uso di un esatto linguaggio matematico indistintamente in ogni settore di ricerca, ma soltanto nel caso che si studino enti immateriali. Perciò un tale modo di esprimersi non si addice all’indagine sulla natura, giacché ogni ente naturale non è certanmente privo di materia.”

Nella tradizione italica, viceversa, il dato sensoriale è solo apparenza; la realtà in quanto essenza è una ricostruzione razionale accessibile solo mediante lo strumento matematico.

L’imperativo per ogni scienza era stato posto da Solone: “Testimonia le cose invisibili con quelle visibili.”

Come possiamo interpretare questa esortazione?

Dato per scontato che le “le cose visibili”, cioè le sensazioni, sono il dato di partenza di qualunque processo conoscitivo, non possiamo fermarci ad esse se vogliamo fare scienza.

Le sensazioni sono semplicemente Caos. Fare scienza significa, quanto meno, dare un ordine alle sensazioni, farne un Cosmos.

Non si può nemmeno riflettere sulle sensazioni senza individuarne alcune, che abbiano un certo grado di stabilità, dando un nome ad esse. Ma questo è solo il principio della scienza.

La scienza deve anche essere in grado di spiegare per essere in grado di prevedere, quindi bisogna cercare “le cose invisibili”, cioè le connessioni intime tra le cose visibili.

È da queste che bisogna partire, non dai sensi.

Ma queste connessioni non possono essere arbitrarie, devono essere “testimoniate”, cioè verificate dai nostri sensi.

Quindi le sensazioni sono il punto di arrivo della scienza non il punto di partenza, al contrario di quello che pensano Aristotele e Mach (per citare alcuni dei più illustri empiristi).

Ma come son fatte le cose invisibili?

Somigliano, forse, all’aria dello “Ionico” Anassimene, che secondo quanto riferisce Ippolito (PR p. 109): “quand’è tutta uniforme, sfugge alla vista, mentre si mostra col freddo e col caldo, con l’umido e il movimento. E si muove sempre perché, se non si muovesse, tutto quel che si trasforma non si trasformerebbe… Sicché i contrari fondamentali per la generazione sono il caldo e il freddo” ?

O non somigliano, piuttosto, alla monade dell’“Italico” Pitagora; che, secondo quanto riferisce Diogene Laerzio (DL VIII, 25)²⁶: “è principio di tutte le cose; dalla monade nasce la diade infinita, che sottosta come materia alla monade che è causa; dalla monade e dalla diade infinita nascono i numeri; dai numeri i punti; da questi le linee, da cui le figure piane; dalle figure piane le figure solide; da queste i corpi sensibili, i cui elementi sono quattro: fuoco, acqua, terra, aria che mutano e si volgono per il tutto, e da questo risulta il cosmo animato, intelligente, rotondo, che contiene al centro la terra anch’essa rotonda e abitata” ?

La contrapposizione è netta. Gli Ionici, seguono una tradizione molto antica che si può far risalire alle prime civiltà neolitiche. Essa sfocerà in quelle che oggi vengono matematizzate sotto il nome di teorie di campo.

Infatti Aristotele dice (PR p. 89): “ritennero che i soli principi di tutte le cose fossero di specie materiale, perché ciò da cui tutte le cose hanno l’essere, da cui originariamente derivano e in cui alla fine si risolvono, pur rimanendo la sostanza ma cambiando nelle sue qualità, questo essi dicono che è l’elemento, questo il principio delle cose e perciò ritengono che niente si produce e niente si distrugge, poiché una sostanza siffatta si conserva sempre… Talete, il fondatore di tale forma di filosofia, dice che è l’acqua.” E Simplicio (PR p. 90) aggiunge che Talete era spinto “a tale conclusione dall’esame sensoriale dei fenomeni.”

Quindi per gli Ionici la realtà non è altro che una determinata materia sensibile che, in qualche modo trasformandosi, dà origine al mondo.

Ma tuttavia, dialetticamente, tra i primi Ionici si ammetteva ancora un principio unitario allo stesso modo degli Italici. Infatti Simplicio (PR p. 90) dice: “Altri supposero un elemento solo e questo dissero illimite per grandezza, come Talete a proposito dell’acqua.” Ed Aezio (PR p. 90): “Talete ed i suoi discepoli dicevano che uno è il cosmo.” E c’è anche il tentativo da parte di Anassimandro di pensare il principio come indeterminato fisicamente, introducendo il termine di infinito; ma secondo Aristotele (PR p. 100) “è chiaro che l’infinito è causa come materia, che la sua essenza è privazione e che il sostrato in sé è ciò che è continuo e sensibile. E tutti gli altri [pensatori], si vede chiaramente, utilizzano l’infinito come materia.” Simplicio (PR p. 109) precisa che “Bisogna sapere che altro è l’infinito e il limitato quanto al numero, il che è proprio di coloro che ammettono molteplicità di princìpi, altro l’infinito e il limitato quanto a grandezza, il che ... conviene ad Anassimandro e ad Anassimene, i quali ammettono sì un unico elemento, ma infinito per grandezza.” Ma nello stesso tempo parlano, secondo Teofrasto (PR p. 109), di rarefazione e condensazione.

Questo è un punto che sarà soggetto alla critica che muovono gli Italici, come vedremo.

Questi, come già detto, seguono la tradizione pitagorica che vuole spiegare le cose del mondo non ricorrendo ai dati sensibili (i quali necessitano di spiegazione essi stessi) ma all’aritmetica e alla geometria.

Proclo (PR p. 118) ci fa sapere che “dopo Talete si ricorda come studioso della geometria Mamerco, fratello del poeta Stesicoro [della città siciliota di Imera] e dopo costoro si dedicò allo studio della geometria e le diede forma di educazione liberale Pitagora, ricercandone i principi primi e investigandone i teoremi concettualmente e teoreticamente: per primo egli trattò poi dell’irrazionale e trovò la struttura delle figure cosmiche.”

Ma anche qui c’è un elemento dialettico, se dobbiamo credere a Diogene Laerzio, il quale, parlando di Pitagora (DL VIII, 14), dice che fu “il primo ad introdurre in Grecia misure e pesi, come dice Aristosseno.”

Il discorso dei Pitagorici è molto più astratto e di più difficile comprensione di quello degli Ionici, specialmente per chi non ha confidenza con la matematica e soprattutto con le applicazioni di essa al mondo fisico. I travisamenti di Aristotele ne sono l’esempio più lampante.

Ma già, all’interno stesso della tradizione pitagorica, avviene una profonda divisione (PR p. 124) tra esoterici (o matematici, o Pitagorici) da una parte ed essoterici (o acusmatici, o Pitagoristi) dall’altra; che in seguito si trasformerà anche in una contrapposizione politica (se pur non sia stato esattamnente il contrario e cioè che la contrapposizione ideologica fosse il risultato di quella politica!)²⁷

Vediamo di interpretare le parole, sopra riportate, con le quali Diogene Laerzio descrive la filosofia di Pitagora.

Facciamo l’ipotesi che si abbia:

monade = ι uno

che, nel linguaggio comune, viene espressa con: la monade è l’uno; ma che più precisamente si dovrebbe esprimere con: la monade è identica al concetto di uno, se interpretiamo uno come una proprietà che diversi individui possono possedere o, invece, (secondo la distinzione terminologica che abbiamo, a suo tempo, introdotta): la monade è identica all’idea di Uno, se, al contrario, pensassimo che Uno sia il nome proprio di qualche individuo esistente, magari nel mondo iperuraneo. La nostra ideografia non è in grado di distinguere tra le due possibili interpretazioni che corrispondono a due diverse metafisiche. Ma dal momento che la proprietà uno si dice di ogni individuo, vale la prima interpretazione e, se Uno esiste, ovviamente Uno ¹ uno e non serve ripetere il ritornello di Aristotele, che uno si dice in molti sensi, se si vogliono evitare le contraddizioni.

Del resto, questa era la polemica che gli Eleati portavano avanti contro i rozzi predecessori di Aristotele.

Notiamo, tuttavia, che si può porre, senza inconvenienti Uno . = . ι uno; ma, in tal caso, bisognerà scrivere “Uno . = . monade” e “monade Î Monade”, con la conseguenza che ci sarebbero infiniti mondi iperuranei.

Ma, naturalmente, in ogni caso si avrà:

uno Î monade ,

cioè: uno è una monade che, senza la distinzione logica che abbiamo chiarito, sembra che dica la stessa cosa di: la monade è l’uno.

I dossografi non sono in grado di afferrare la differenza tra individuo ed elemento (tra άτομον e μονάς) per cui riportano (vedi PR p. 489): “Archita e Filolao chiamano indifferentemente l’uno anche monade e la monade uno.”

Molto probabilmente, invece, i due Pitagorici menzionati volevano mettere in evidenza la diversità formale tra la proprietà e l’elemento che ne è il suo concetto.

Ma i dossografi sono ormai sotto la cappa del vocabolario antiscientifico creato da Aristotele il quale, anche se in qualche modo aveva intuito la profonda differenza della semantica pitagorica rispetto a quella degli Ionici, non riesce a liberarsi dal concreto sensibile e dalla sua logica grammaticale; dice infatti nella Metafisica (PR p. 520): “I principi e gli elementi di cui si servono i filosofi che sono detti Pitagorici, sono assai lontani da quelli dei fisiologi. E la causa è in questo, che essi non li hanno presi dalle cose sensibili; gli enti matematici infatti, se si eccettuano quelli che riguardano l’astronomia, sono senza movimento.”

La concezione degli enti matematici di Aristotele oggi appare infantile, se confrontata a quella dei Pitagorici che andava criticando; per cui egli si sorprende che i Pitagorici li potessero applicare all’indagine sulla natura ed allo studio delle cose percepibili. E si chiede stupefatto in che senso si deve intendere che il numero e le proprietà dei numeri sono causa delle cose che sono.

Per capire cosa mai i Pitagorici intendevano dire, useremo le notazioni di Peano.

Indichiamo comì “ x” un individuo che appunto è uno e indivisibile come l’ άτομον dei greci.

Con indivisibile dobbiamo intendere l’oggetto pensato come indiviso, cioè in quanto individuo anche se, per altri aspetti, può essere divisibile all’infinito.

Si pensi al termine “retta”: possiamo pensare la retta come individuo indivisibile componente di uno spazio fatto di rette o come insieme di punti e quindi divisibile all’infinito.

Nel linguaggio formale bisognerà usare due simboli diversi per i due concetti se, nel contesto in cui se ne parla, servono entrambi: se “P” è la proprietà “punto”, “ áP ” sarà la comprensione di “P” e cioè la proprietà “insieme di punti”. Cioè: “P . = . punto” e “ áP . = . insieme di punti”.

Supponiamo che “R . = . retta”. Sarebbe errato scrivere: “R É P” in quanto si avrebbe per sillogismo (nella sua forma singolare) “x Î R . É . x Î P”, cioè, se “ x” è una retta allora “x” è un punto.

Bensì, dobbiamo scrivere: “R É áP”, che dà origine a: “x Î R . É . x Î áP”

(ovvero: “x Î R . É . x É P”), cioè se “x” è una retta allora x è un insieme di punti.

Ma, nello stesso tempo, avremo: “ι x Î áR . É . ι x Î ááP” cioè, “ι x” è il concetto di una data retta “x”; “x”, invece, è una tra le proprietà possibili degli insiemi di punti, cioè della comprensione del concetto insieme di punti, e, a sua volta, il concetto insieme di punti è la comprensione del concetto punto.

Nel linguaggio ordinario, con il termine “retta” si intendono entrambe le cose e non si possono evitare le contraddizioni.

Allo stesso modo, se scriviamo: x Î monade avremo x = uno; ma se scriviamo: ι x Î monade (monade=elemento=concetto di essere uno), dobbiamo intendere ι x . = . uno e quindi: x Î ι x . = . x Î uno e, ancora: x = x . = . x Î uno. Cioè, se qualcosa è una monade essa è l’uno e, invece, quella cosa di cui predichiamo che è una, è sempre uguale a se stessa e viceversa.

Di nessun concetto (o idea) noi possiamo predicare che non è uno; perché arriveremmo alla conclusione assurda che “x ¹ x”. Quindi se qualcosa è un concetto o un’idea, allora è una.

Ma, dal momento che la vera realtà, l’essenza delle cose tutte, sono i concetti, allora se qualcosa “è” allora essa è una. E, allo stesso tempo, “uno” sarà molti, anzi infinito, essendo che infiniti sono gli individui dell’estensione del suo concetto. Asserzione che verrà, poi, ribadita dagli Eleati.

Tale asserzione esprime il fatto ovvio che qualsiasi idea o concetto è uno, financo il concetto di pluralità. E, viceversa, qualsiasi proprietà che non sia un’idea singolare è molti, come la stessa proprietà di essere uno.

Abbiamo convenuto che uno è una proprietà, infatti, non esiste alcun individuo di cui “Uno” sia il nome proprio.

Ma una volta che ci siamo formati il concetto di uno, per contrapposizione logica, acquistiamo anche il concetto di non-uno, che può essere o semplice molteplicità, cioè numero, o l’infinito cioè il non numerabile (nel senso che non è possibile assegnargli un numero —ne viene che i numeri interi, essendo infiniti, non sono numerabili; contrariamente alla definizione odierna, originatasi dalle ipotesi di Cantor) ottenendo così la “diade”, cioè la coppia (uno;non-uno) che perciò viene detta “infinita” dai Pitagorici, in quanto ogni cosa è uno o non-uno.

Quindi la “diade” non è l’idea di due.

Tuttavia gli individui della diade sono due; ma tali due individui sono proprietà complementari delle cose tutte.

Lo stesso vale per qualsiasi altra proprietà. In altre parole, tutte le volte che introduciamo una nuova proprietà, se essa non è la proprietà assurda (il non-essere) o la proprietà banale (l’essere), allora esisteranno individui che hanno la proprietà complementare. Quindi tutto il mondo viene generato (logicamente) dalle coppie di contrari di cui i Pitagorici ne fanno un lungo elenco a scopo esemplificativo.

Ma non tutte le proprietà sono attribuibili all’uno in quanto individuo della monade perchè molte altre proprietà sono attribuibili solo agli individui che hanno la proprietà di essere uno o non-uno, che sono tutti gli individui del mondo (fisico o logico che esso sia).

Ma se limitiamo il campo di ricerca, identificando la diade con la totalità delle cose che sono nello spazio (la monade coinciderà, in questo caso, con il concetto di punto), avremmo:

diade =(punto;non-punto) e gli individui elementari sarebbero solo gli indivisibili punti.

Con ciò abbiamo creato un’altra diade di enti contrapposti e cioè la contrapposizione concreto-astratto; per cui l’individuo, in quanto pensato come essere concreto, “sottostà come materia alla monade che è causa” ovvero elemento, (o anche: principio, forma, idea, essenza, sostanza, ecc, che sono gli svariati termini con i quali, nel fluire dell’entropia durante il corso dei secoli, si è tradotto il termine greco αιτία o gli altri termini con i quali Aristotele crede di spiegare il predetto termine).

Che questa nostra interpretazione possa essere la più corretta (necessità logica a parte) viene confermato da certe parole dello stesso Aristotele, là dove dice (PR p. 512-13): “Al tempo di costoro [Leucippo e Democrito], si dedicarono alle matematiche e per primi le fecero progredire quelli che son detti Pitagorici. Questi, dediti a tale studio, credetterro che i principi delle matematiche fossero anche principi di tutte le cose che sono [notiamo che i princìpi delle matematiche sono princìpi “logici”]. Or poiché principi delle matematiche sono i numeri [questa ci sembra una personale opinione di Aristotele; infatti, per i Pitagorici non c’è differenza fra numeri e rapporti tra grandezze; e tutte le cose del mondo hanno grandezze fisiche; e solo mediante queste le descriviamo! infatti i Pitagorici:] vedevano espresse dai numeri [perfino] le proprietà e i rapporti degli accordi armonici ... hanno pensato che due sono le cause i Pitagorici, ma essi hanno in più pensato, e in questo è la loro singolarità, che il limitato e l’infinito e l’uno non siano attributi degli altri enti, come il fuoco e la terra e qualunque altra cosa simile a questi, ma che lo stesso illimitato e lo stesso uno siano la sostanza delle cose che da essi sono predicate [infatti fuoco Î uno uno Î predicato = essenza = causa = elemento = sostanza = ...] ... di numeri compongono l’intero cielo; ma non di numeri formati da unità senza grandezza, ché essi attribuiscono grandezza alle unità. ... Dicendo che sostanza è l’unità, e non la cosa di cui si dice che è una, Platone è d’accordo coi Pitagorici; e ancora s’accorda con essi quando dice che i numeri sono causa dell’essere delle altre cose [cioè sono proprietà delle cose che sono]. Suo proprio è invece l’aver sostituito la diade all’infinito concepito come uno, e aver creduto che l’infinito consti del grande e del piccolo [infatti, per i Pitagorici, l’infinito è qualunque cosa sia diverso dal niente, dall’uno e dal molti, indipendentemente dal fatto che sia grande o piccolo, i punti di un granellino di sabbia sono infiniti come quelli dell’intero universo fisico]. Inoltre egli pose i numeri fuori delle cose percepibili, mentre essi dicono che le cose stesse sono numeri [infatti, p. es., gli occhi dell’uomo “sono” 2 e gli occhi sono cose! Se ne diamo un’altra interpretazione, bisognerà pensare che i Pitagorici fossero dei deficienti! ma questo proprio non sembra!], e non pongono nel mezzo gli enti matematici [da Platone indebitamente ipostatizzati!]. Questo, il porre, diversamente da quanto fanno i Pitagorici, l’uno e i numeri fuori delle cose, e introdurre le specie egli potè fare perchè nella ricerca si serviva della dialettica, che i filosofi precedenti non conoscevano”.

Con il significato odierno di dialettica diremmo che i filosofi precedenti erano dialettici, mentre Platone era assolutamente adialettico, a meno che per dialettica non si intenda la possibilità di asserire contemporaneamente due asserzioni contraddittorie, come spesso viene intesa.

Ma come mai dai “numeri” nascono i “punti”?

Questo ce lo faremo spiegare dal pitagorico Archita (PR p. 491): “S’io mi trovassi all’estremità dello spazio, ad esempio nel cielo delle stelle fisse, potrei tendere la mano o un bastoncino fuori di quella? o non potrei?”

Se consideriamo come unità di misura il bastoncino (o la mano, in tal caso parleremmo di un “palmo”), con l’esempio di Archita avremmo generato la serie dei numeri interi e al limite l’infinito. La domanda di Archita non è altro che un modo di enunciare il principio di induzione matematica così come formalizzato da Peano. Ma il bastoncino lo possiamo dividere in sottomultipli sempre più piccoli e al limite, otterremmo i “punti”.

È divertente, a questo proposito, osservare l’incapacità di Aristotele di pensare i numeri come riferibili alle grandezze fisiche; al più, ed ovviamente sbagliando, identifica l’unità con il punto (PR p. 516): “Anche i Pitagorici pensano che il numero sia d’un modo solo, e cioè [numero] matematico ...Di numeri infatti compongono l’intero cielo; ma non di numeri senza grandezza, ché essi attribuiscono grandezza alle unità” e più oltre, avendo stabilito, invece, che almeno le unità non possono avere grandezza essendo indivisibili (non si capisce perchè!), si chiede attonito: “com’è possibile che una grandezza sia composta da indivisibili? E tuttavia il numero è formato da unità. Essi invece dicono che il numero è le cose che sono, o almeno applicano i loro teoremi ai corpi, come se i numeri fossero corpi”.

Ma per Pitagora di punti si compongono le “linee” e di queste le “figure piane” e di queste, a loro volta, le “figure solide”.

Ed in che altro modo potremmo descrivere i “corpi sensibili” se non con questi strumenti matematici?

Forse che “fuoco, acqua, terra, aria” non sono corpi sensibili?

E tuttavia essi assumono forme geometriche ed hanno grandezza!

Basterà aggiungere il movimento per ottenere il “cosmo animato e intelligente”. Intelligente perché concepito dalla nostra intelligenza.

Tale filosofia è stata in seguito praticata da Democrito e da Archimede ed è stata esplicitamente enunciata da Galileo asserendo che la natura è un libro aperto ma che i suoi caratteri sono figure geometriche.

Ma ecco il concetto centrale: il “cosmo animato” creato dall’intelligenza, la quale si contrappone al caos informe delle sensazioni.

Il concetto di ordine è fondamentale per il cosmo; nella lingua greca i due concetti hanno lo stesso nome. Aezio (PR p. 131) dice: “Pitagora fu il primo a chiamare cosmo la sfera delle cose tutte, per l’ordine che esiste in essa.”

È molto probabile che il concetto di ordine derivasse da quello di legge scritta che dalla sfera sociale veniva estesa alla sfera naturale. Nella Storia del mondo antico della Cambridge University Press, lo storico P.N. Ure, in relazione al fatto che le prime legislazioni scritte nel mondo di lingua greca si devono ai legislatori pitagorici Zeleuco di Locri e Caronda di Catania, scrive: “Nelle comunità di fondazione relativamente recente della Magna Grecia e della Sicilia le costumanze inveterate erano indubbiamente considerate meno sacrosante che nella madrepatria, circostanza che può spiegare il ruolo eminente che queste regioni ebbero nel mutamento importantissimo rappresentato dall’introduzione di codici scritti.”

Che le cose nella mente di Pitagora fossero legate assieme è testimoniato da Diogene Laerzio il quale riferisce che egli scrisse tre libri: Dell’educazione, Del governo delle città, Della natura.

Ma questo della natura non è un ordine statico in quanto il cosmo è animato, cioè dotato di movimento. Questa semplice idea rende logicamente impossibile la concezione del mondo propria degli Ionici la quale, a sentire Teofrasto (PR p. 138), fu anche ripresa dall’ex pitagorico Ippaso (il quale sembra che abbia organizzato una rivolta politica all’interno delle città rette dai Pitagorici): “Anche Ippaso di Metaponto ed Eraclito di Efeso dissero che l’uno è mosso e limitato, ma pensarono come fuoco il principio, e dissero che dal fuoco nascono le cose per condensazione e per rarefazione, e che in esso poi le cose si dissolvono, perché questa sola è per essi la natura che fa da sostrato.”

Ma per capire come tale assunzione sia in assoluto contrasto con le teorie pitagoriche bisognerà seguire la linea consequenziale del pensiero degli Italici emergente dal poema Sulla Natura scritto da Parmenide (PR p. 271):

“Orbene io ti dirò e tu ascolta attentamente le mie parole,

quali vie di ricerca sono le sole pensabili:

l’una dice che è e che non è possibile che non sia,

è il sentiero della Persuasione (giacchè questa tien dietro alla Verità);

l’altra dice che non è e che non è possibile che non sia,

questa io ti dichiaro che è un sentiero del tutto inindagabile:

perché il non essere né lo puoi pensare (non è infatti possibile),

né lo puoi esprimere.”

Prima di riportare questi versi Sesto Empirico premette: (PR p. 268) “Il suo [di Senofane] discepolo Parmenide condannò il discorso di opinione, cioè quello costituito di rappresentazioni non salde, e pose come criterio il discorso scientifico, cioè quello che non può essere rovesciato, rifiutando ogni credibilità alle sensazioni.” E Simplicio (PR p. 269) dice: “Questi uomini posero una duplice ipostasi: l’una ciò che realmente è, l’intelligibile; l’altra ciò che diviene, il sensibile, che non credettero di chiamare essere assoluto, ma essere apparente. Ragione per cui dicono che dell’essere c’è verità di ciò che diviene opinione.”

Mettiamo le affermazioni di Parmenide in simboli: Nella via della Persuasione e della Verità (oggi diremmo della Logica) se asseriamo “ $a” dobbiamo asserire necessariamente “a ¹ Ù” ; e non possiamo asserire “ ~$a” e nello stesso tempo “a ¹ Ù”.

Se, d’altra parte, astraiamo da qualsiasi proprietà “a”, come in seguito penserà di poter fare Aristotele introducendo il suo multiforme e perciò ambiguo concetto di ούσία , ci ridurremmo alla “proprietà banale” posseduta da tutte le cose e alla sua complementare, la “proprietà assurda” che nessuna cosa (nemmeno puramente ideale) può possedere, come si è visto nelle sezioni precedenti.

Ed infatti il poema parmenideo continua:

“Bisogna che il dire e il pensare sia l’essere: è dato infatti essere,

mentre nulla non è; che è quanto ti ho costretto ad ammettere.

Da questa prima via di ricerca infatti ti allontano,

eppoi inoltre da quella per la quale mortali che nulla sanno

vanno errando, gente dalla doppia testa. Perchè è l’incapacità che nel loro

petto dirige l’errante mente; ed essi vengono trascinati

insieme sordi e ciechi, istupiditi, gente che non sa decidersi,

da cui l’essere e il non essere sono ritenuti identici

e non identici, per cui di tutte le cose reversibile è il cammino.”

Quindi per Parmenide la descrizione (“il dire e il pensare”) della realtà coincide con la realtà stessa (“l’essere”); il resto è “nulla”; cioè, 1’ingannevole effetto di sensazioni informi (prive di alcuna individuabile proprietà):

“Ma tu da questa via di ricerca allontana il pensiero

né l’abitudine nata dalle molteplici esperienze ti costringa lungo questa via,

a usar l’occhio che non vede e l’udito che rimbomba di suoni illusori

e la lingua, ma giudica col raziocinio la pugnace disamina che io ti espongo. ...”

L’essere, in quanto tale, è un ente della logica, cioè del nostro modo di esprimerci e pertanto non ha senso dire che ha un’origine o una fine; esso

“Essendo ingenerato é anche imperituro,

tutto intero, unico, immobile senza fine.

Non mai era né sarà, perché è ora tutt’insieme,

uno, continuo. Difatti quale origine gli vuoi cercare?

Come e donde il suo nascere? Dal non essere non ti permetterò né

di dirlo né di pensarlo. Infatti non si può né dire né pensare

ciò che non è. E quand’anche, quale necessità può avere spinto

lui, che comincia dal nulla, a nascere dopo o prima?

Di modo che è necessario o che sia del tutto o che non sia per nulla.

Giammai poi la forza della convinzione verace concederà che dall’essere

alcunché altro da lui nasca. Perciò né nascere

né perire gli ha permesso la giustizia disciogliendo i leganmi,

ma lo tien fermo. La cosa va giudicata in questi termini;

è o non è. Si è giudicato dunque, come di necessità,

di lasciare andare l’una delle due vie

come impensabile e inesprimibile (infatti non è la via vera)

e che l’altra invece esiste ed è la via reale.

L’essere come potrebbe esistere nel futuro?

In che modo mai sarebbe venuto all’esistenza?

Se fosse venuto all’esistenza non è e neppure se è per essere nel futuro.

In tal modo il nascere è spento e non c’è traccia del perire.

Neppure è divisibile, perchè è tutto quanto uguale.

Né vi è in alcuna parte un più di essere che possa impedirne la contiguità,

né un di meno, ma è tutto pieno di essere.

Per cui è tutto contiguo: difatti l’essere è a contatto con l’essere.”

Ne consegue che parlare di un principio materiale, unico, limitato ed in continuo movimento, con condensazioni e rarefazioni, come fanno Eraclito ed il Pitagorista Ippaso (i fisici, oggi, chiamerebbero la concezione del mondo di costoro una Teoria di Campo) è un’assurdità, perchè l’essere se è essere non può che essere limitato, immobile, omogeneo, isotropo e senza tempo. Tali proprietà si possono solo attribuire ad un insieme di punti indifferenziato; solo quando ne considerassimo anche la proprietà della estensione fisica diventerebbe lo spazio assoluto di Newton, che poi è lo spazio come modellato dalla geometria.

Infatti l’essere è

“... immobile ... senza conoscere né principio né fine ... E rimanendo identico nell’identico stato, sta in sé stesso ...”.

In quanto l’essere è un costrutto logico non ha senso il dire che è illimitato, altrimenti sarebbe “incompiuto” e “manchevole”; la qual cosa è impossibile perché non esistono punti che non siano punti dell’essere: “... infatti la dominatrice Necessità lo tiene nelle strettoie del linmite che tutto intorno lo cinge ...”.

Per introdurre il concetto di spazio illimitato abbiamo bisogno di introdurre altre proprietà oltre a quella primordiale di essere, come già detto.

Senza di queste

“saranno tutte soltanto parole ... nascere e perire, essere e non essere, cambiamento di luogo e mutazione del brillante colore.”

In assenza di altre proprietà non c’è niente che possa cambiare nella sola proprietà di essere. E l’essere

“è compiuto da ogni lato, simile alla massa di ben rotonda sfera ... che egli infatti non sia né un pò più grande né un pò più debole qui o là è necessario ... né c’è la possibilità che l’essere sia dell’essere qui più, là meno, perché è del tutto inviolabile.”.

A questo punto siamo costretti a osservare che se identifichiamo l’essere con la materia, esso non potrebbe muoversi senza vuoti frapposti, ma allora l’essere sarebbe e nello stesso tempo non sarebbe; sarebbe uno e, nello stesso tempo, molti. Ma ciò è contro la logica.

Aristotele crede di superare la ferrea logica di Parmemmide opponendo che l’essere si dice in molti sensi. Ed è vero! Ma è proprio questo che Parmenide vuole superare! cioè l’ambiguità ed i molteplici sensi delle parole della lingua comune, legata al sensibile e non adatta per un discorso veramente scientifico.

Ma come, a partire dalla logica di Parmenide, possiamo spiegare l’apparenza dei sensi?

“Con ciò interrompo il mio discorso degno di fede e i miei pensieri

intorno alla verità; da questo punto le opinioni dei mortali impara

a conoscere, ascoltando l’ingannevole andamento delle mie parole.

Perchè i mortali furono del parere di nominare due forme,

una delle quali non dovevano — e in questo sommo andati errati —;

ne contrapposero gli aspetti e vi applicarono note

reciprocamente distinte: da un lato il fuoco etereo

che è dolce e leggerissimo, del tutto identico a se stesso,

ma non identico all’altro, e inoltre anche l’altro [lo posero] per sé

con caratteristiche opposte, [come] notte senza luce, di aspetto denso e pesante.

Quest’ordinamento cosmico, apparente come esso è, io te lo espongo compiutamente,

cosicchè non mai assolutamente qualche opinione dei mortali potrà superarti.”

A partire da questo punto, solo pochi sconnessi frammenti ci rimangono della titanica opera parmenidea. Non ci resta che continuare con la sua ferrea logica.

Per spiegare il mondo dei sensi, quindi, dobbiamo introdurre altre proprietà che non possono essere di natura logica come quella dell’essere. In contrapposto al logico, porremo il materiale.

Allora, tra i punti dell’essere ci saranno i punti materiali e quelli non-materiali cioè i punti dello spazio vuoto di materia; cioè, il “vuoto”, il quale “esiste” alla stessa stregua della materia. Perché sia i punti materiali che i punti privi di materia sono punti dello spazio fisico che coinciderà con l’essere se gli individui del nostro campo di ricerca sono solo essi.

“Queste cose, benché lontane, vedile col pensiero saldamente presenti:

non infatti distaccherai l’essere dalla sua connessione con l’essere

né quando sia disgregato in ogni senso completamente con cura sistematica

né quando sia ricomposto.”

Si intende nella sua reale unità di essere pensato; anche se prima o dopo lo possiamo ripensare “completamente disgregato” come costituito di punti materiali che si muovono nello spazio geometrico. E questo è quello che concretamente ha fatto Archimede (vedi rifer. di cui a nota²⁰).

Si può concludere che per Parmenide una Teoria di Campo è logicamente autocontraddittoria ed è solo possibile una Teoria di Particelle come sarà succesivamente precisata da Leucippo e Democrito, i quali secondo Diogene Laerzio seguono, appunto, la tradizione italica.

Ma prima di passare a questi ultimi giganti, è bene seguire le conseguenze della critica parmenidea alle concezioni dei fisici dell’opposta scuola di pensiero, come formalizzate dal suo discepolo Zenone.

Atomi e vuoto.

Notiamo intanto che, con l’impostazione che abbiamo esposto, cade qualunque divieto per l’uso della matematica nella descrizione fisica della realtà, sia di tipo aristotelico che, come abbiamo visto, relega la matematica allo studio di enti privi di materia e privi di movimento; sia alla proibizione misticheggiante di tipo platonico.²⁸

Anzi, per capire la realtà fisica, in quanto sintesi di materia e movimento, dobbiamo indagare a fondo sugli enti matematici, che per gli Italici, non sono avulsi dalla realtà ma semplicemente astratti dalle impressioni sensoriali e che, anzi, costituiscono, ormai, la realtà stessa. Per essi non avrebbe alcun senso una matematica chiusa su se stessa che non si curi di sapere di quali enti concreti si occupi.

Per loro non c’è differenza tra geometria e fisica. E non è vero che per essi gli assiomi della geometria siano autoevidenti di per sé, come la maggior parte dei commentatori moderni asserisce, attribuendo ai “Greci” il modo di ragionare di Aristotele, ma sono semplicemente quelli che meglio si adattano a fungere da mattoni per il sistema deduttivo. Per esempio, non serve, in questa logica, negare l’assioma delle parallele per lo spazio fisico, perché la sua asserzione è compatibile con tutte le osservazioni empiriche.

Diogene Laerzio attribuisce a Zenone la dottrina che “Esiste un solo mondo e il vuoto non esiste”; ma molto probabilmente, nella distorsioime postaristotelica, Diogene confonde il mondo con l’essere, cioè con la proprietà banale (mentre per Zenone il mondo è l’essere materiale) e il vuoto con la privazione di essere, cioè con la proprietà assurda (mentre per Zenone il vuoto è l’essere privo di materia).

Infatti abbiamo visto che per il suo maestro Parmenide l’essere non è materiale ma logico e solo in questo senso è uno. Del resto questo viene riconosciuto anche dallo stesso Aristotele (PR p. 256).²⁹

Ed è la stessa rozza filosofia di Antistene (di cui alla nota precedente) che impedisce ad Aristotele e ai dossografi di capire gli argomenti di Zenone.

Con Zenone siamo meno fortunati, in quanto i frammenti pervenutici sono pochissimi e le testimonianze sono inaffidabili, data l’opposta metafisica dei commentatori.

Ma abbiamo visto che i frammenti di Parmenide sono compatibili con la logica della matematica così come formalizzata da Peano e, per coerenza, dobbiamo postulare che il discepolo e difensore dell’opera del maestro usi la stessa logica e, quindi, dobbiamo assumere che i suoi discorsi fossero costruiti per ridurre all’assurdo le tesi degli antagonisti.

Esaminiamo prima le conseguenze logiche dei postulati che abbiamo attribuito a Parmenide ed a tutta la tradizione pitagorica.

L’“ente” in quanto essere sensibile, oltre alla proprietà di “essere” (cioè di essere costituito dai punti dello spazio delle cose che esistono fisicamente ovvero la materia e di essere costituito dai punti dello spazio privi di materia, ovvero il vuoto) deve avere altre proprietà che lo rendono sensibile e cioè estensione fisica caratterizzata da proprietà (massa, volume, forma, densità, ecc.) che ne diversificano le diverse parti. A tali proprietà sono associate delle grandezze che le misurano.

Senza di queste l’ente non è niente (cioè ni-ente=non-ente); come, del resto, testimonia Simplicio (PR p. 302-03) riportando un frammento di Zenone: “In questa argomentazione poi mostra che ciò che non possiede né grandezza né spessore né massa alcuna neppure esiste. Dice:

Se infatti venisse aggiunto a un altro essere non lo renderebbe per nulla maggiore. Difatti, non avendo esso grandezza alcuna, quando venga aggiunto non é possibile che nulla aumenti in grandezza. E cosi senz’altro ciò che venne aggiunto non sarebbe nulla. Se poi, quando venga sottratto non diventerà per nulla minore, e neppure, d’altro canto, quando quello venga aggiunto questo diventerà maggiore, è chiaro che non era nulla né ciò che venne aggiunto né ciò che venne sottratto.

E questo Zenone non lo dice per negare l’uno, ma perché ognuno dei molti e infiniti ha grandezza ...”.

E tale grandezza è divisibile all’infinito (PR p. 303): “Se esiste è necessario che ciascuna cosa abbia una certa grandezza e spessore e che in essa una parte disti dall’altra. Lo stesso ragionamento vale anche della parte che sta innanzi: anche questa infatti avrà grandezza e avrà una parte che sta innanzi. Questo vale in un caso come in tutti i casi: nessuna infatti di tali parti sarà l’ultima e non è possibile che non ci sia una parte a precedere l’altra. Così, se [tali parti] sono molte, è necessario che esse siano piccole [in grandezza] e grandi [in numero]: piccole fino a non avere grandezza, grandi fino ad essere infinite [in numero]³⁰.

La continuità dell’essere (indipendentemente dal fatto che i singoli punti siano punti di essere solido e indivisibile o di essere fatto di pori contigui, come precisa l’italico Empedocle,³¹) è, per Zenone, una necessità logica e non l’eventuale risultato di un’impossibile osservazione empirica:

“Se gli enti sono molti é necessario che siano tanti quanti sono e non più né di meno. Ma se sono tanti quanti sono saranno limitati.

Se gli enti sono molti sono infiniti: sempre infatti in mezzo agli enti ve ne sono altri e in mezzo a questi di nuovo degli altri. E in tal modo gli enti sono infiniti.”

O, in altre parole, se gli “enti” in quanto essere sensibile fossero numerabili (“molti”)³² verrebbero ad essere non numerabili. Quindi per evitare contraddizioni logiche dobbiamo ammettere che anche l’essere sensibile è uno e continuo nella sua essenza, anche se ci appare come costituito di parti che si diversificano nelle varie proprietà che ne definiscono l’estensione fisica.

Se lo spazio fisico è quello che, per via di pura logica, è stato delineato (che altro non è che lo spazio newtoniano!) non ha senso parlare di “luogo” che contiene le cose come in un vaso (secondo la similitudine aristotelica).³³

Infatti, Zenone dice (PR p. 304): “Ciò che si muove non si muove né in quel luogo in cui è, né in quello in cui non è”. In quanto sono le proprietà dei punti dello spazio che si modificano, non nel senso che il singolo punto sia più o meno denso di materia come nelle teorie di campo, che sono state dimostrate logicamente contraddittorie da Parmenide; ma nel senso che nel corso del tempo il singolo punto è dotato o meno della proprietà di essere materia o di essere vuoto.

La proprietà di essere più o meno denso è solo apparenza, in quanto proprietà di tutto un sistema di punti e solo “in media” di un determinato punto.

Aristotele, nella sua Fisica, spende decine e decine di pagine credendo di poter contestare Zenone aggiungendo parole confuse a parole di cui non ne comprende il significato. Ma non riesce a venirne a capo, passando da una contraddizione all’altra. E, alla fine, se ne tira fuori ricorrendo al Deus ex machina (di cui ne contestava, invece, l’uso nell’arte drammatica) costituito dalla sua ineffabile distinzione tra atto e potenza.

Ma, con l’ultima citazione zenoniana, si esauriscono i frammenti di Zenone, come raccolti dal Diels-Kranz (vedi PR). Saremo costretti a seguire Aristotele servendoci solo della logica, ma non certamente della logica aristotelica!

Per Aristotele, Zenone appare il negatore di ogni movimento. Ma la verità è che Zenone negava la possibilità logica del movimento se si fossero assunte le ipotesi che la lingua comune assumeva e che Aristotele ha cercato di giustificare con l’arricchire la lingua comune di altri termini di significato ancora più ambiguo di quelli che voleva spiegare.

Nel linguaggio comune si ipostatizza una contrapposizione netta tra numeri e grandezze.

I numeri sono il regno del discreto, le grandezze quello del continuo.

I numeri sono fatti di unità e le unità sono indivisibili.

Le grandezze sono divisibili all’infinito.

I Pitagorici affermavano, invece, che i numeri sono rapporti tra grandezze, come abbiamo visto che lo stesso Aristotele testimonia.

Ma, secondo lui, non sembra che essi sappiano dire come sia composta la prima unità dotata di grandezza (naturalmente questo non è vero come dimostra il ragionamento di Archita, precedentemente da noi citato, da cui emerge chiaramente che per i Pitagorici il numero non è altro che il risultato dell’operazione di misura delle grandezze per confronto con l’unità di misura. E, quest’ultima è nello stesso tempo unità e grandezza).

Ma questo per Aristotele è inconcepibile (PR p. 516-17):

“Il modo [di concepire il numero] dei Pitagorici comporta meno difficoltà di quelle di cui ho parlato finora, ma ne comporta altre sue proprie. Perché, se il concepire il numero come non separato [dalle cose] elimina molte difficoltà, assurdo è tuttavia dire che i corpi sono composti di numeri e concepire nello stesso tempo questi numeri come matematici. È infatti errato parlare di grandezze indivisibili: e, d’altra parte, se sono soprattutto in questo modo [come grandezze], almeno le unità non hanno grandezza. Ora com’è possibile che una grandezza sia composta di indivisibili? E tuttavia il numero è formato di unità.”

Ecco da dove proviene l’assurdo! Per Aristotele, le grandezze sono sempre divisibili, le unità sono indivisibili, quindi le grandezze e i numeri sono inconciliabili. D’altra parte, anche i punti sono indivisibili e quindi sono unità, per cui i corpi non possono essere composti di punti, come concluderà nella Fisica, ricorrendo alla finzione, di natura puramente verbale, che i punti sono il limite e le grandezze il limitato.

Questa, in seguito a complicatissimi (e senza senso) ragionamenti, porterà Aristotele a concludere (Fisica 218a 18, 19): “In realtà, si deve ritenere impossibile che gli istanti siano continui tra loro, come è impossibile la continuità tra punto e punto.”

Ma, nello stesso tempo, per Aristotele, l’istante separa i due tempi prima e dopo il movimento e il punto separa i due luoghi dove si trovava l’oggetto prima e dove si troverà dopo il movimento.

Ma Aristotele, dopo che in varie opere ha enunciato che la cosa più certa è che non si può affermare contemporaneamente una proprietà e la sua contraria, risolve il problema dicendo che: “l’istante è in parte identico e in parte non identico” (Fisica 219b 32).

Ma se si assumono tali ipotesi, il moto risulta impossibile logicamente; e questo è quello che Zenone dimostra.

Primo argomento: Se punti e istanti non sono continui l’intervallo tra di essi, comunque piccolo, sarà una grandezza finita. Allora, supponiamo che bisogna percorrere una lunghezza finita in un tempo finito. Cadremmo subito in contraddizione, perché per percorrere la lunghezza bisognerà prima percorrerne la metà. E poi la metà della metà. E così via di seguito per un numero infinito di volte. Quindi, per l’ipotesi che gli intervallini sono finiti, occorrerà un tempo infinito e la distanza stessa risulterà infinita.

Aristotele crede di superare l’argomento dicendo che il rapporto di due grandezze infinite può essere finito (Fisica 233a 13-28):

“... risulta ovvio che, se il tenmpo è continuo, lo è pure la grandezza, se è vero che nella metà di un dato tempo si percorre la metà di una data grandezza e, insomma, in un tempo minore una grandezza minore: identiche, infatti, saranno le divisioni del tempo e quello della grandezza, e se uno qualsivoglia dei due è infinito, lo sarà anche l’altro; e nel modo in cui è finito il primo, nello stesso modo lo sarà anche l’altro; ad esempio, se il tempo è infinito per le estremità, anche la grandezza lo sarà per estremità; e se quello è infinito nella divisione, nella divisione sarà infinita anche la grandezza; e se il tempo è infinito in ambedue le guise, sarà infinita anche la grandezza in ambedue le guise.

Anche per questo il ragionamento di Zenone erroneamente presuppone l’impossibilità che si possano percorrere gli infiniti o che possano toccarsi ciascuno successivamente in un tempo finito. Difatti, tanto la grandezza quanto il tempo e, in generale, ogni cosa continua si dicono infiniti in due sensi, cioè o per divisione o per gli estremi. Pertanto, gli infiniti che son tali secondo la quantità, non possono toccarsi in un tempo finito; quelli, invece, che son tali secondo divisione, lo possono, perché il tempo stesso è infinito sotto questo aspetto.”

Il ragionamento di Aristotele dice cose banali se riferite al moto uniforme, false se riferite al moto in generale come da lui considerato, ma soprattutto trascura di ricordare il fatto più importante che per lui non c’è continuità né tra gli istanti né tra i punti, per cui ogni grandezza infinita per divisione deve risultare, necessariamente, anche infinita per gli estremi. Nella sezione successiva sembra ricordarsene, ma per uscirne ricorre alla incomprensibile dialettica tra potenza e atto. Il teorema di Zenone resta in piedi tutto intero.

Ma era quello, che noi abbiamo posto, il problema di Zenone?

Non lo potremo mai sapere!

Ma possiamo fare delle ipotesi sulla cultura matematica di Zenone in base alla tradizione che abbiamo descritto e ai pochi frammenti che ci rimangono; cose che depongono a suo favore. Nello stesso tempo, abbiamo la prova inequivocabile della incapacità di ragionamento scientifico che dimostra Aristotele in tutti i suoi scritti. Ma lo stesso Aristotele ci dà un indizio (PR p. 295):

“Allo stesso modo bisogna opporsi a quelli che ci fanno obbiezioni conformi al ragionamento di Zenone [e ritengono] che se si deve pur sempre percorrere la metà, e se queste metà sono infinite, non si può percorrere l’infinito, o anche ad altri che ci fanno obiezioni in maniera diversa, ma conformi pur sempre a quello stesso ragionamento, ritenendo che, nello stesso tempo in cui avviene il movimento nella metà del percorso, si deve prima numerare la metà che risulta da ciascuna metà, sicchè, mentre l’oggetto percorre l’intero, accade che esso abbia numerato un numero infinito: cosa che, per comune consenso, è riconosciuta impossibile.”

Secondo argomento: detto Achille. Niente di nuovo rispetto al primo, come ci dice Aristotele, a parte “il fatto che la grandezza successivamente assunta non viene divisa per due” dal momento “che chi insegue giunga in precedenza là di dove si mosse chi fugge”; e a parte la drammaticità del fatto che la tartaruga non potrà mai raggiungere il pié veloce Achille.

Su questo argomento, i commentatori moderni attribuiscono a Zenone l’affermazione che non è possibile ottenere una lunghezza finita come somma di una serie infinita, dimenticando anch’essi di assumere, come viene esplicitamente assunto da Aristotele, il “se” esistono “unità indivisibili” (che non sono la stessa cosa degli “indivisibili”; infatti i punti sono indivisibili ma non sono unità e le unità (in quanto unità di misura) sono grandezze e sono sempre divisibili. Quindi la contraddizione viene dall’assunzione già contraddittoria che esistano unità indivisibili, che è ciò che appunto Zenone voleva dimostrare ricorrendo al ragionamemmto per assurdo).

Terzo argomento: La freccia scoccata dall’arco non si muove, se, ovviamente, si fa l’ipotesi, che è anche di Aristotele, che la freccia occupa un luogo che trasporta con se come un vaso e inoltre diciamo, come dice Aristotele, che un corpo è fermo quando occupa il suo luogo, cioè uno spazio uguale al corpo stesso. Ma in ogni istante questo è vero; quindi, per definizione, il corpo è fermo in ogni istante e quindi sempre. Aristotele crede di poter superare la contraddizione negando che il tempo sia costituito da istanti. Ma questo è palesemente assurdo e Aristotele se ne esce dicendo che in un senso l’istante è nel tempo e in un altro senso no per via del solito sotterfugio della potenza e dell’atto a cui ora si deve aggiungere un’ancora più misteriosa entelechia che rende perfetto l’atto. Amen.

Quarto argomento: “è quello delle masse uguali che si muovono lungo masse uguali in senso contrario, le une dalla fine dello stadio, e le altre dalla metà con uguale velocità. In esso crede che si provi che sono un tempo uguale il tempo metà e il tempo doppio. Il paralogismo consiste in questo, nel ritenere che con la stessa velocità si percorra nello stesso tempo ha stessa grandezza presa in un caso lungo un mosso e nell’altro lungo un immobile. Questo invece è falso.” (PR p. 298).

Verissimo! ma, al solito Aristotele, si dimentica di dire che con le sue ipotesi, più volte qui sopra ricordate, le due velocità devono essere uguali! Non ha senso contestare un teorema cambiando le ipotesi lungo la strada! Ma, per Aristotele, la fisica è una cosa che percepiamo con i sensi e la logica e la matematica sono un’altra cosa, da usare solo per fare discorsi con parole senza alcun significato. Come del resto avviene oggi per i cosiddetti logici o metamatematici moderni.

Con il contestatissimo Zenone si può terminare qui.

Dopo di lui, entro la stessa tradizione, viene un altro grande scienziato, naturalmente molto inviso ad Aristotele, si tratta dell’agrigentino Empedocle. Anche se, in questo caso, i frammenti pervenutici non sono pochi, la loro natura esula dal problema che stiamo trattando.

Possiamo però affermare che il suo discorso scientifico sta dentro la tradizione italica, come del resto testimoniato da quasi tutti i dossografi e non si capisce perchè Aristotele, spesso, lo contrappone agli altri.

È interessante la testimonianza di Neante, riportata da Diogene Laerzio (PR p. 325) che “fino a Filolao e ad Empedocle i Pitagorici comunicavano le loro dottrine; ma che quando Empedocle le rese pubbliche attraverso la poesia, stabilirono la norma che non fossero comunicate a nessun poeta (e questo dice che dovette subirlo anche Platone: anche costui infatti ne restò escluso).”

Naturalmente questo ci appare inevitabile nel constatare come Platone abbia deformato le loro dottrine continuando ad autodefinirsi Pitagorico.

Per Aristotele (PR p. 347) il poema di Empedocle non è molto comprensibile:

“Se la dissoluzione avrà un termine, il corpo in cui si arresterà sarà o un atomo o bensì divisibile, ma tale che nel fatto non sarà mai diviso, come sembra voler dire Empedocle”.

Queste cose che “sembra” voler dire Empedocle saranno chiarite da Democrito che fa parte della stessa tradizione come sappiamo per mezzo di Diogene Laerzio che parlando dell’abderita dice (PR p. 665): “Sembra, dice Trasillo, che egli sia stato un grande ammiratore dei Pitagorici, anzi fa menzione dello stesso Pitagora, parlandone con ammirazione nell’opera che s’intitola dal nome di lui. E parrebbe che Democrito avesse tratto da Pitagora tutte le dottrine e che ne fosse stato anche scolaro, se la cronologia non facesse ostacolo. Che in ogni modo però egli sia stato alla scuola dei Pitagorici, ci è attestato da Glauco di Reggio, vissuto nella stessa epoca di Democrito. E anche Apollodoro di Cizico dice che frequentò Filolao.”

Dobbiamo ritenere che nello stesso periodo circolavano due opposte interpretazioni delle dottrine pitagoriche, quella di Platone e quella di Democrito e questo spiegherebbe quello che riferisce Diogene Laerzio (DL p. 367-68): “Aristosseno nelle sue Memorie Sparse afferma che Platone ebbe l’intenzione di bruciare tutte le opere di Democrito che potè raccogliere, ma che i pitagorici Amicla e Chinia lo distolsero dal suo proposito, in quanto non ne avrebbe tratto utilità alcuna, perché ormai i libri erano ampiamente diffusi nel pubblico. E ciò è chiaro. Infatti, Platone, che pure menziona quasi tutti i filosofi arcaici, non accenna mai a Democrito neppure là dove avrebbe dovuto contraddirlo, evidentemente perché era consapevole che avrebbe dovuto gareggiare col migliore dei filosofi, che anche Timone non potè fare a meno di lodare ...”

Resta il problema di capire perché quasi tutta l’opera di Platone è arrivata fino a noi e niente della copiosa opera di Democrito ci è pervenuta. Un’ipotesi per questo apparente miracolo sarà avanzata nella prossima sezione.

Stranamente, pochissimi sono i frammenti genuini di Democrito ma moltissime le testimonianze il più delle volte distorte o male interpretate.

Ma dai pochissimi frammenti è indubbio che egli esprime la filosofia e la scienza della tradizione italica.

Sesto Empirico riporta il seguente frammento (PR p. 748): “Opinione il dolce, opinione l’amaro, opinione il caldo, opinione il freddo, opinione il colore; verità gli atomi e il vuoto.”

Cioè le sensazioni sono solo opinione perciò fallibili, i costrutti logici di atomi e vuoto sono la realtà scientifica.

Infatti Galeno, che è uno scienziato, commenta tali parole (PR p. 688): “ritenendo che tutte le qualità sensibili, ch’egli ritiene relative a noi che ne abbiamo sensazione, derivano dalla varia aggregazione degli atomi, ma che per natura non esistano affatto bianco, nero, giallo, rosso, dolce amaro: infatti l’espressione ‘per convenzione’ [vόμω] equivale, per esempio, a ‘secondo l’opinione comune’ [vόμιστί] e a ‘relativamente a noi’ [πρός ήμάς], cioè non secondo la natura delle cose, la quale egli indica con l’espressione ‘secondo verità’ [έτεή] ricavata da έτεόυ, che significa ‘vero’. E tutto il senso di questo discorso sarebbe il seguente: gli uomini credono che sia qualche cosa di reale il bianco e il nero, il dolce e l’amaro, e tutte le altre qualità del genere, mentre in verità ente e niente = non-ente sono tutto ciò che esiste, perché Democrito usava anche questi termini, chiamando ‘ente’ gli atomi e ‘niente’ il vuoto. Così tutti quanti gli atomi, essendo corpi piccolissimi [oggi diremmo punti materiali o particelle elementari], non posseggono qualità sensibili, ed il vuoto è uno spazio nel quale tali corpuscoli si muovono tutti quanti ...”.

Lo stesso Democrito, secondo Sesto Empirico, dice (PR p. 749), ripetendo in prosa la teoria che Parmenide aveva espresso in versi:

“Vi sono due forme di conoscenza, l’una genuina e l’altra oscura; e a quella oscura appartengono tutti quanti questi oggetti: vista, udito, odorato, gusto, tatto. L’altra forma è la genuina, e gli oggetti di questa sono nascosti [alla conoscenza sensibile e oscura]. Quando la conoscenza oscura non può più spingersi ad oggetto più piccolo né col vedere né coll’udire né coll’odorato nè col gusto nè con la sensazione del tatto, ma ási deve indirizzar la ricercañ a ciò che è più sottile, áallora soccorre la conoscenza genuina, come quella che possiede appunto un organo più fine, appropriato al pensareñ”.

Più d’uno tra i dossografi testimonia che Democrito chiama idee gli elementi e i principi delle cose che sono. Gli atomi sono gli individui, cioè gli indivisibili di tali idee. E in quanto una porzione di spazio è materia in modo continuo, essa è solida cioè indivisibile fisicamente (senza pori) e anch’essa si comporta come un atomo, in quanto non può avere qualità sensibili (che sono generate dalla mescolanza di atomi e vuoto mediante l’interazione con i nostri sensi, anch’essi composti di atomi e vuoto).

Di questi solidi niente possiamo sapere senza opportuni modelli particolari da verificare con opportuni esperimenti, se non quello che possiamo dedurre per via puramente logica e cioè che essi possono differire solo per forma e volume e per la posizione che occupano nello spazio. E dal punto di vista logico, possono essere piccoli quanto si vuole (ma non di grandezza nulla) e grandi quanto il mondo.

La loro massa, finchè sono solidi sarà, necessariamente, proporzionale al volume, perché non c’è motivo che la densità della materia indistinta e priva di vuoto sia diversa da un solido all’altro.

Da queste ipotesi Democrito sviluppa tutta una scienza integrata che ci appare, nonostante le distorsioni dei commentatori, come moderna e grandiosa perché ricavata solo al lume della logica, astenendosi da ipotesi azzardate, quando la logica ne lasciasse aperte più possibilità.

Infatti Democrito raccomanda (PR p. 784): “Non sforzarti per sapere tutte le cose, perché c’è il rischio che tu finisca ignorante su tutte”.

Ma, nello stesso tempo, inizia la sua opera intitolata Piccola Cosmologia (PR p. 784):

“In questa trattazione discorro di tutte le cose ...

In altre parole: Evita di sapere Tutto su Nulla come lo specialista di Bernard Show e nello stesso tempo evita di sapere Nulla su Tutto come i tuttologi radiotelevisivi. Affidati solo alla ragione e non fare ipotesi azzardate che non siano testimoniate dai sensi.

In base a questa regola, quali possibilità esistono per il moto degli atomi?

Riferisce Simplicio (PR p. 681): “Del fatto che le sostanze rimangano in contatto tra di loro per un certo tempo, egli dà la causa ai collegamenti e alle capacità di adesione degli atomi.”

E qui Simplicio dà un elenco di possibilità, oggi, tutte spiegabili con le forze molecolari.

Ma come avviene la disaggregazione?

“ …egli reputa dunque che gli atomi si tengano attaccati gli uni agli altri e rimangano in contatto solo fino a quando, col sopraggiungere di qualche azione esterna, una necessità più forte non li scuota violentemente e li disperda in varie direzioni”.

Ma da dove può provenire l’azione esterna se tutto l’essere è formato da atomi e vuoto? Dai commentatori non lo sappiamo perché ipotizzano cose contraddittorie ma la logica ci dice che gli atomi, necessariamente, interagiscono tra loro. Anche Newton sembra essere della stessa opinione.³⁴

Ma Aristotele pensa che nel ragionamento di Democrito si nasconde un paralogismo perché (PR p. 684): “Noi vediamo lo stesso corpo, saldamente unito, presentarsi ora allo stato liquido, ora solidificato, senza che si sia verificata in esso separazione o riunione di parti, e senza che ciò si debba alla direzione o al contatto reciproco, come dice Democrito: perché il corpo da liquido si trasforma in solido senza ‘spostamento interno’ e senza ‘modificazione della sua struttura’.”

Chiaramente Aristotele è condizionato dagli organi dei sensi e non riesce ad usare il senso più sottile che è quello della ragione che opera secondo la logica che non è quella grammaticale di Aristotele.

Per Democrito che usa tale organo si ha, invece, (PR p. 682): “Se dunque il nascere è aggregazione di atomi e il dissolversi è disgregazione, anche per Democrito il divenire non è che modificazione di stato” che può aversi solo per ‘modificazione della struttura’ interna dei corpi proprio causata dallo ‘spostamento interno’.

Ma vediamo ancora, in un’altra importante questione, come Democrito usa la logica della matematica per mostrare l’assurdità delle unità indivisibili e la necessità dei punti indivisibili (PR p. 780): “Se un cono viene secato da un piano parallelo alla base, come si dovranno immaginare le superficie di sezione? verranno uguali o disuguali? Perché, se saranno disuguali, renderanno irregolare il cono che verrà ad avere tante incisioni e scabrosità a gradini; ma se saranno uguali le superfici saranno uguali anche le sezioni e il cono verrà ad assumere l’aspetto del cilindro, in quanto risultante dalla sovrapposizione di cerchi uguali e non disuguali: il che è manifestanaente assurdo”.

Ecco perché Archimede mostra grande stima per Democrito (PR p. 780): “Perciò appunto anche circa questi teoremi sul cono e sulla piramide, di cui Eudosso ha trovato per primo la dimostrazione, e cioè che il cono è la terza parte del cilindro e la piramide del prisma che abbiano la medesima base e uguale altezza, non piccola parte di merito è da attribuire a Democrito che per primo formulò, senza dimostrazione, l’enunciato relativo alle figure suddette”.

Notiamo che Archimede, dicendo senza dimostrazione, intende semplicemente senza l’uso del metodo (detto di esaustione) di Eudosso. Ma il merito di Democrito è “non piccolo” perchè ha usato il concetto dei punti indivisibili e Archimede ne sa qualcosa, come risulta dal suo Metodo Meccanico! (vedi rifer. di cui a nota²⁰).

Mito e scienza.

Da quanto detto, analizzando la scienza dei cosiddetti presocratici, emerge che Platone e Aristotele rappresentano un profondo, incommensurabile arretramento nell’evoluzione del linguaggio scientifico. Quindi è chiaro che la teoria delle PULCI non è valida. Ci resta da capire il perché.

Dobbiamo cercare di individuare i meccanismi che producono l’andamento fluttuante dell’efficacia del linguaggio a descrivere la realtà.

Abbiamo accennato, nel Preambolo, che tali meccanismi sono esterni al sistema della scienza e hanno radici sociali ed economiche.

L’azione di tali meccanismi, la si può osservare seguendo la nascita, lo sviluppo e la morte dei linguaggi scientifici anche nelle più antiche civiltà della storia umana.

Si può ipotizzare un coerente modello per descrivere l’evoluzione di tali linguaggi. Ma prima è necessario sgombrare il campo dai secolari (o, forse, millenari!) pregiudizi creati dal mito di quella che abbiamo chiamato la teoria delle PULCI, dalla quale si può solo dedurre che gli antichi scienziati non potevano essere molto di più che promettenti bambini; mentre, esaminando le cose a fondo, si affaccia prepotentemente alla mente il fondato sospetto che la profondità e l’ampiezza del loro pensiero non era per niente inferiore a quella dei più grandi geni della nostra era e di gran lunga superiore a quella, inesistente, dei falsi profeti.

Infatti, riesce difficile poter conciliare le sbalorditive conoscenze di matematica, fisica e astronomia dei popoli della valle del Nilo o di quelli delle regioni attorno al Tigri ed all’Eufrate (come testimoniate da papiri e iscrizioni scoperti negli ultimi due secoli; conoscenze che si fanno risalire a più di mille anni prima di Talete, considerato il progenitore della scienza Greca) con le sciocchezze che Aristotele ed i suoi successori fanno dire agli eredi di lingua greca di tali popoli e cioè ad Italici e Ionici.

Per tale ragione faremo l’ipotesi, che oggi potrebbe apparire rivoluzionaria ma che già era stata adombrata ai tempi di Pitagora da Teagene di Reggio, secondo la quale, a brevi periodi particolarmente felici in cui si ha un effettivo progresso scientifico susseguano lunghi periodi di caligine in cui si perde persino la capacità di capire quello che, nel periodo precedente, era stato conquistato spesso a caro prezzo.

Naturalmente, questo non avviene per caso; perchè un sistema, ormai corrotto, di simboli serve a proteggere la classe che detiene il dominio del potere e della “CULTURA”, pur se di questa se ne possa mantenerne il nome (ad ogni buon conto ed a scanso di equivoci, le abbiamo riservato l’onore dei caratteri maiuscoli non potendo qui abusare di quelli cubitali).

Infatti, per fare solo alcuni tra i mille possibili esempi, come spiegare il fatto che, nonostante le immense conquiste scientifiche di Egizi e Mesopotamici, in Ionia ed in Italia, agli albori della civiltà greca, si deve praticamente ripartire da zero? E, ancora, come spiegare, altrimenti, il fatto che Ionici ed Italici, dopo enormi conquiste riescono a raggiungere le vette della scienza archimedea e, nonostante ciò, Galileo e Newton devono ripartire anch’essi quasi da zero?

Le spiegazioni che usualmente se ne danno non hanno né capo, né coda come acutamente osserva il Farrington,³⁵ il quale, giustamente, propone una spiegazione fondata sulla struttura sociale e politica.

Noi, qui, ci proponiamo di ampliare questa tesi, mostrando lo stretto legame tra le strutture sociali e le strutture linguistiche della scienza.

Il reggino Teagene, intorno al 500 a. c., difende Omero dall’accusa di essere dannoso e sconvenientemente irriguardoso verso gli dèi adducendo che i miti omerici non riguardavano gli dèi, in quanto i nomi ad essi attribuiti stavano a rappresentare le concrete forze della natura. Certo, ai tempi dell’ovviamente altrettanto sacrilega scienza pitagorica della natura, e particolarmente a Reggio, dove allora Teagene scriveva, egli si poteva permettere una tale difesa di Omero; trovandosi in un posto ed in un’epoca tra quelle fortunate, se pur brevi, in cui risulta possibile la pratica e lo sviluppo della scienza; chissà se l’avrebbe potuto nell’Atene di Socrate!

Si potrebbe attribuire un senso politico al mito, riportato da Filodemo, secondo il quale il poeta ed indovino Epimenide diceva che le Arpie figlie di Oceano e di Gea furono uccise presso Reggio!

Ma, per ironia della sorte, sono rinate da quelle parti, costringendo proprio a Reggio gli ultimi Pitagorici, scacciati a forza dalle loro città-Stato.

Ma, a noi, resta il problema di sapere perché Omero sentiva la necessità di nascondersi dietro il nome degli dèi dell’Olimpo!

Non sarà forse la stessa ragione per cui qualcosa sembra anche nascondersi nei miti attribuiti ad Orfeo, il quale viene spesso associato ai Pitagorici?

Nel coro degli uccelli di Aristofane si sente l’eco della teogonia orfica:

“Il Caos e la Notte, l’Erebo oscuro, il Tartaro immenso primi regnarono;

né Terra, né Aere, né Oceano potevano esistere ancora;

ma dentro gli sterminati spazi di Erebo

un uovo senza seme, per primo, le buie ali della Notte partorirono;

si susseguirono le stagioni ed emerse da questo l’amabile Eros,

dal tergo splendente di ali dorate, qual vortice d’uragano

egli si unì al Caos alato; nella notte del Tartaro sconfinato,

il genere dei mortali fu creato e portato alla luce.

Non esistevano ancora gli dèi immortali, prima che Eros accoppiasse le cose.

Ma quando ogni cosa all’altra fu accoppiata, Urano e Oceano comparvero

e Terra; e, degli altri dèi, l’intera progenie immortale.

Proviamo a interpretare tali versi secondo il suggerimento di Teagene:

Prima che l’uovo senza seme, cioè l’uomo in quanto astratto dal suo substrato materiale, in quanto pensiero, potesse condurre i mortali alla luce del sapere, l’universo appariva disordinato; era semplicemente Caos, sterminato come il Tartaro, informe come l’Erebo e buio come la Notte. Prima che la mente dell’uomo distinguesse le cose, l’idea stessa di materia, nei suoi tre stati di aggregazione: solido, liquido e gassoso (= Terra, Oceano ed Aria), non era nemmeno pensabile.

Solo dal primigenio pensiero può sorgere l’idea di Eros, cioè della connessione intima di cose contrapposte tra loro (l’idea dei contrari dei Pitagorici cantata nei versi di Empedocle, da cui può nascere, in seguito, anche l’idea di attrazione reciproca tra cariche di opposta polarità). Questa, unendosi all’idea di materia ancora informe, ma in eterno movimento, rappresentata dal Caos alato, col susseguirsi delle stagioni, porta i mortali dalla notte dell’ignoranza alla luce del sapere. Non può esistere il concetto di immortale senza quello, di origine empirica, di mortale. Infatti, nei versi di Aristofane, gli dèi nascono dopo!

Solo così si possono creare i concetti scientifici (gli dèi immortali) di cielo, di mare e di terra (=Urano, Oceano e Terra). Tali concetti, in quanto concetti, possono essere creati solo dopo che siano nati gli uomini, con la luce del loro intelletto, ma ogni concetto è, per sua natura, eterno come, necessariamente sarà successivamente, anche l’Essere di Parmenide.

E qua Aristotele e soci scoprirebbero un’aporia: come è possibile che siano eterni e quindi increati se sono stati creati dall’uomo? Naturalmente, questo lo ipotizziamo perché Aristotele non riesce mai a distinguere il concetto da quello che esso rappresenta. La nostra stupida domanda sembra molto simile a quella che porta al paradosso di Russell. È lo stesso che chiedersi come può essere immortale il nome “immortale” che l’uomo stesso ha inventato?!

Che il mito orfico si riferisse alla spiegazione razionale e soprattutto logica dell’universo è testimoniato dall’altro grande poeta greco Euripide che nell’Alceste, riferendosi alle tavolette di Orfeo di Tracia, canta:

Io, grazie alle Muse,

mi son librato in alto,

ho esaminato ogni discorso,

ma, della Necessità, niente di più cogente

ho potuto scoprire, né altro si può ricavare

dalle tavolette di Tracia

che la voce di Orfeo ha dettato...

Ricordiamo che Euripide ha difeso con i suoi versi il suo amico Anassagora accusato di empietà.³⁶

La spiegazione orfica della natura percorre tutta la scienza dei cosiddetti presocratici, dove, di volta in volta, se ne mette in luce un qualche aspetto particolare, molto probabilmente, per controbbattere le obiezioni più stupide che ad essa si venivano facendo. Anche se fra tali obiezioni ce ne potevano essere di più serie e meritevoli di essere considerate e superate; come di fatto sono state via via superate. Per esempio, il ruolo della necessità logica, menzionata nei versi di Euripide, sarà di fondamentale importanza nella scienza degli Italici e culminerà nella ferrea logica di Parmenide e del suo discepolo Zenone.

Tradizionalmente, dato che solo in anni relativamente recenti si sono decifrati i papiri e le tavolette di Egizi e Mesopotamici, la nostra scienza si fà cominciare da Talete. Questi riduce il principio di tutte le cose all’acqua.

Questa visione, se dobbiamo fare l’ipotesi che i dossografi riportino correttamente, sembra un regresso rispetto al mito orfico echeggiato da Aristofane.

L’ipotesi che i dossografi riportino correttamente sembra altamente improbabile. Infatti costoro in massima parte si limitano a riportare le opinioni di Platone o di Aristotele, spesso anche peggiorandone il senso; ma quasi sempre d’accordo con i paradigmi interpretativi di questi due personaggi che si sono imposti nei secoli bui della scienza.

Tuttavia, alla luce dei risultati e delle credenze della scienza galileiana, esaminando le critiche che, con una presunzione inaudita, i due “sommi filosofi” rivolgono agli scienziati che li avevano preceduti nel tempo, appare manifesta la loro assolutamente bambinesca concezione del mondo che, in nessun modo, può reggere il confronto con la profondità di pensiero di tutti i loro predecessori. E per capire questo bastano le loro stesse critiche!

E ciò, come crediamo di avere mostrato, risulta pienamente confermato dai pochissimi frammenti che di tali antichissimi veri scienziati ci sono pervenuti.

Potrebbe apparire sorprendente ed addirittura misterioso il fatto che di tutti gli scienziati, anteriori, contemporanei o anche posteriori a Platone e ad Aristotele, niente o quasi ci sia pervenuto; mentre di questi due campioni abbiamo quasi tutto quello che hanno scritto e, forse, anche qualcosa che non hanno scritto, visto che sono infinite le diatribe sull’autenticità di alcune loro opere. Ma, alla luce della su accennata legge dell’entropia, sarebbe sorprendente se fosse successo il contrario.

Proviamo a chiederci quali opere resteranno tra mille anni a partire da oggi?

Naturalmente non i libri di scienza, la cui diffusione è irrisoria in confronto ai libri che hanno un mercato! Il pronostico si può fare facilmente esaminando il mercato dei libri o le vetrine dei librai!

***

Per tornare alle prove contrarie alla teoria delle PULCI, supponiamo, solo per un momento, che il pensiero dei presocratici sia giusto quello che dai dossografi ricaviamo.

Allora per spiegare il regresso degli Ionici rispetto ai miti orfici, come reinterpretati alla luce dell’ipotesi di Teagene, ci rimarrebbero pochissime possibilità.

Accettando la tradizione che vuole Talete di stirpe fenicia e che, a detta di Flavio, “Ferecide di Siro, Pitagora, Talete, furono per ammissione generale discepoli degli Egizi e dei Caldei” allora o la scienza di Egizi e Caldei era meno avanzata di quella tramandata dai miti orfici o l’armamentario culturale di Talete non era sufficientemente adeguato per capire appieno la scienza di quei popoli. Si dovrebbe scartare la seconda ipotesi dal momento che Proclo dice che Talete fece molte scoperte nel campo della geometria che aveva appreso in Egitto e, d’altra parte, Plutarco (PR p. 89) dice che i sacerdoti egizi “pensano che anche Omero, come Talete, pose l’acqua inizio e matrice di tutte le cose, avendolo appreso dagli Egizi: infatti Oceano è Osiride, Tetide è Iside ...”.

Certo, pensando che la civiltà degli Egizi, come quella dei Caldei, si è sviluppata in assoluta dipendenza dai fiumi attorno ai quali vivevano, si potrebbe ritenere che l’acqua potesse essere vista come l’elemento primordiale.

Ma questa rozza concezione del mondo contrasterebbe con le meravigliose conquiste scientifiche oggi abbondantemente documentate dai ritrovamnenti scritti (tenuto conto della legge, sopracennata che i libri si conservano proporzionalmente alla loro diffusione, legge confermata empiricamente in tutti i ritrovamenti presso i resti delle civiltà sepolte).

Del resto, sembra accertato che la scienza della Mesopotamia, dopo uno sviluppo notevole nel corso di pochi secoli, ristagnerà per millenni, fino alla totale distruzione.

Come scrive un noto storico della scienza antica,³⁷ si hanno due gruppi di testi relativi alla matematica mesopotamica che corrispondono a due periodi nettamente delimitati e molto lontani tra loro. Il primo va dal 1800 a.C. al 1600 a.C., il secondo si riferisce agli ultimi tre secoli a.C. (per la maggior parte, tavolette che dovevano servire come libri di scuola o altre di contabilità relativa ai commerci del tempo).

Pochi sono i mutamenti che si possono osservare passando da un gruppo all’altro e nel secondo gruppo non vi interviene alcun principio nuovo che non fosse già pienamente utilizzato nel periodo precedente. Per cui il Neugebauer conclude: “E’ consuetudine postulare un lungo sviluppo, che si suppone necessario, per raggiungere un alto livello di intuizione matematica. Non so su quale esperienza si basi un giudizio del genere. Tutti i periodi, storicamente noti, di grandi scoperte matematiche hanno raggiunto il loro apice dopo uno o due secoli di rapidi progressi, preceduti e seguiti da molti secoli di relativo ristagno.”

Del resto, anche in tutti gli altri campi della cultura, si nota un decadimento della cultura Assira e Babilonese rispetto a quella dei Sumeri, loro predecessori in Mesopotamia.³⁸

Non può essere un caso che i maggiori progressi scientifici, sia nella Ionia, sia nella Magna Grecia, sia nella Mesopotamia si abbiano in corrispondenza di una organizzazione socio-economica fondata su pacifiche città-Stato.

Sia in Mesopotamia, nel passaggio dalle sumeriche citta-Stato agli imperi AssiroBabilonesi, che in Grecia, nell’anologo passaggio all’egemonia ateniese, si osserva nella cultura un parallelo passaggio dal naturalismo spontaneo, che si riflette nelle credenze religiose, ad un più stretto rigore moralistico che accentua la trascendenza del divino; ma lo stesso fenomeno trova conferma nella storia di tutte le civiltà.

Questo si riscontra nei miti sumerici confrontati con quelli babilonesi. Spesso, basta una semplice trasposizione dei nomi degli dèi per ottenere lo stesso significato dei miti delle diverse civiltà anche lontane tra loro nello spazio e nel tempo.

Tuttavia, spesso, gli storici della scienza si affannano nel cercare di sminuire le conquiste del passato, ciò al solo scopo di far tornare i conti con la teoria delle PULCI.

A che punto siamo oggi?

Siamo nella fase della Scienza o in quella del Mito?

Per il momento lasciamo al lettore la risposta a tale arduo quesito.

Appendice.

Un sistema di logica.

Diamo qui di seguito un elenco di formule, già riportate nei vari lavori di logica scritti dal Peano (cfr. OS-II e FM)³⁹, ordinate in modo da costituire uno tra i possibili sistemi deduttivi che dalle formule di Peano si possono estrarre.

Lo scopo è quello di dare un esempio concreto di sistema deduttivo e un riferimento immediato per le formule che si incontrano nel testo. Per tale ragione sono state introdotte alcune lievi modifiche nei segni usati dal Peano per renderli omogenei alle convenzioni adottate nel testo.

***

Termini, descrizioni e assiomi della metalogica:

Termini:

= significa significa.

C . = . proprietà.

I . = . individuo.

P . = . proposizione.

Î . = . è un (copula).

É . = . implica (deduzione).

∩ . = . e (congiunzione).

. = . proprietà complementare dell’intersezione delle proprietà “a” e “b”.

Simboli: le lettere minuscole dell’alfabeto italiano.

Assiomi:

(M1) ,

(M2) x Î a . É . x Î I ∩ a Î C ∩ (x Î a) Î P,

(M3) ,

(M4) ιa Î C ,

(M5) a Î C . É . áa Î C .

Definizioni, assiomi e teoremi della logica.

Termini primitivi: Î, ι, á, ~, Ù.

Descrizioni:

Î . = . è un… .

ι . = . identico a … .

á . = . proprietà che implica la … .

~ . = . incompatibilità tra due proprietà o proposizioni.

Ù . = . proprietà assurda o proposizione assurda.

Definizioni:

(A1) = .=. Î ι

(A2) É .=. Î á

(P1)

(Q1)

(A3)

(A4) a_x .=. x Î a

(A5) Î_x a .= . a_x

(A6) '_x a_x .=. a

(A7)

“Ú” significa la proprietà banale cioè quella proprietà che è posseduta da qualunque individuo o (negli altri contesti appropriati) la tautologia cioè la proposizione necessariamente vera.

(P2)

(Q2)

(P3)

(Q3)

(P4)

(Q4)

Assiomi :

(P5)

(Q5)

(P6)

(Q6)

(P7)

(Q7)

(P8)

(Q8)

(P9)

(Q9)

(P10)

(Q10)

(P11) a É b . = . ab = a

(Q11) a_x É b_y . = . a_xb_y = a_x

La formula (Q11) non si trova in Peano; ma non è da arguire che possa essere asserita in base al calcolo proposizionale di Whitehead e Russell (nel seguito li indicheremo con la sigla WR).

Infatti, la (Q11) ha un significato affatto diverso da quanto viene asserito in tale calcolo, in quanto non si riferisce a proposizioni categoriche, come per i succitati autori, ma a schemi di proposizioni.

Ricordiamo che, per Peano, le proposizioni categoriche non fanno parte della logica (cfr. OS-II p. 314).

Notiamo intanto che il segno “É” (che possiamo leggere “implica”) ha un significato profondamente diverso dall’implicazione materiale di WR e, d’altra parte, non corrisponde nemmeno alla loro implicazione formale, la quale corrisponde al segno “É_x” di Peano, che è definito dall’identità:

(a1) a, b Î Cls . É: . a É b . =: x Î a . É_x .x Î b .

Cioè, se “a” e “b” sono classi (=proprietà) allora dire che l’estensione di “a” è inclusa nell’estensione di “b” è lo stesso che dire che, per ogni individuo “x”, “x Î a” implica “x Î b” (vedi FM p. 7), avendo, tuttavia, fatto la convenzione che le estensioni definiscano completamente le proprietà (come chiarito nella Parentesi epistemologica).

Nel calcolo delle classi di Peano il segno di inclusione “É” rappresenta una “relazione” tra proprietà (analoga al segno “£“ tra numeri) e, quindi, per la (al), lo stesso vale per l’implicazione formale “É_x”.

Nella formulazione di WR (che è quella che successivamente si è affermata) il segno di implicazione materiale, indicata sempre col segno “É”, rappresenta un’“operazione” (analoga al segno “+” tra numeri), essendo definita dalla

├─ (p É q = ~ p U q)

dove “p” e “q” sono proposizioni arbitrarie.

Ricordiamo che per WR il segno “├─ a” indica che la proposizione “a” viene asserita e non semplicemente menzionata (colle convenzioni di Peano, che qui abbiamo seguito, non è necessario introdurre un segno speciale per le asserzioni in quanto ogni proposizione della logica si intende, non solo asserita, ma addirittura come “necessariamente asserita”; essendo che la logica elenca solo proposizioni che sono necessariamente vere e non solo semplicemente vere e non elenca proposizioni false se non per negarle quando siano delle contraddizioni).

Quindi, WR non pretendono nemmeno che si abbia:

(a2) ├─ (p É q = ├─ ~ p U q)

Mentre la (Q11) vale [vedi appresso (T21)]:

(a3) a_x É b_y . = . ã_x U b_y = Ú

cioè, esplicitando interamente le nostre convenzioni: “a_x É b_y” è, per definizione, la stessa cosa che dire che la proposizione “ã_x U b_y” è “necessariamente vera”.

Resta da capire in che modo una proposizione relativa ad un individuo “x” possa essere collegata in modo necessario ad una proposizione relativa ad un altro individuo “y”; ma questo lo si potrà vedere, in seguito, con l’introduzione delle diadi.

Diamo intanto alcuni assiomi che servono a collegare le proprietà alle proposizioni:

(C1) (ab)_x . = . a_xb_x

(C2) xÎa . = . ι x Î áa . = . i x É a

(C3) a_x ∩ (a É b) . É . b_x

Questa rappresenta la forma individuale del sillogismo. La (C3) viene data, spesso, come assioma ma si potrebbe (vedi appresso T23) dimostrare come teorema a partire da (C2) e dal sillogismo in forma universale (vedi appresso T22) che si dimostra, indipendentemente, a partire dagli altri assìomi.

Sono utili anche i seguenti assiomi:

(C4) a Î áb . = . áa Î ááb . = . áa É áb

(C5)

(C6) x Î a . É . $a

(C7)

Con l’introduzione delle “diadi” si può ricondurre al formalismo generale delle proprietà anche quello delle relazioni.

Consideriamo una relazione arbitraria, p.es., quella che abbiamo indicato col segno “Δ, e supponiamo di volere esprimere simbolicamente l’idea che che la coppia di simboli “x” e “a” stiano nella relazione “x Î a”. Considerando la “diade” “(x; a)” (coppia ordinata in cui “x” è il primo termine e “a” il secondo) come un singolo individuo, possiamo scrivere “(x; a) Î R_Δ asserendo che “R_Î Î R” e “R . = . relazione” che quindi, per (M2), diventa una proprietà (“R É C”)

Avendo indicato col termine (costante) “R_Δ la proprietà che un qualsiasi individuo “x” ha di possedere una data proprietà “a”.

Cioè, nel nostro caso particolare, possiamo scrivere “(x; a) Î R_Î . = . x Î a”.

Allo stesso modo, possiamo definire “(x; y) Î R₌ . = . x = y”, “(a; b) Î R_É . = . a É b”, “(a; b) Î R_∩ . = . a ∩ b”, ecc.

Si potrebbe formalizzare il tutto in modo affatto generale ma, per i nostri scopi, ciò non è necessario.

È ovvio che, a partire dalle diadi, si possono definire le triadi: “(x; y; z) . = . ((x; y); z)” e così via, per qualsiasi insieme totalmente ordinato con un numero qualsiasi di simboli.

Con queste convenzioni possiamo, p. es., senza bisogno di altri assiomi, ricondurre la (C3) ad una forma particolare della (Q11).

Basterà, usando la (A2), riscrivere la (C3) come: “a_x ∩ (áb)_a . É . b_x” e, ricorrendo al formalismo delle triadi, avendo posto “(x; a; b) Î R^á . = . a_x ∩ (áb)_a ”, per la (Q11) possiamo scrivere “R^á_(x;a;b) É b_x . = . R^á_(x;a;b) b_x = R^á_(x;a;b)”.

Questo ci fa capire, anche, in che senso un’implicazione tra proposizioni singolari può esprimere una necessità logica, cioè una tautologia e ancora, in connessione con la (T20), ci mostra come non sia necessaria una logica modale come calcolo separato. Infatti le modalità vengono fuori dal significato che abbiamo attribuito al segno “$”.

Con ciò, perdono di significato le logiche intuizionistiche e le altre diavolerie del genere (vedi PF).

***

Regole deduttive:

Dl. Da ogni singolo schema di proposizione valido della logica si può dedurre un altro schema valido sostituendo ad un suo simbolo, qualsiasi altro simbolo, purchè la sostituzione venga effettuata in ogni posto dello schema in cui compaia il primo simbolo.

D2. Da ogni schema di proposizione valido della logica si può dedurre un altro schema valido sostituendo ad un suo simbolo, un altro simbolo che risulti identico al primo, per via di qualche proposizione valida del sistema.

D3. Da ogni identità valida del sistema deduttivo (x = y) si ottiene un’altra identità valida (ωx = ωy) operando su ambo i membri dell’identità con un operatore (ω) per il quale abbia senso applicarlo su uno dei due membri della prima identità.

Per la defizione di identità e per le regole deduttive valgono sempre gli schemi seguenti:

(I1) a = a

(I2) a = b . = . b = a

(I3) (a = b) ∩ (b = c) . = . (a = c)

A partire dalle definizioni e dagli assiomi precedenti si possono dimostrare moltissimi teoremi, usando tali regole deduttive.

Tuttavia è importante ricordare che per Peano i teoremi della logica sono, in generale, evidenti di per sé; per cui lo scopo della dimostrazione non è quello di assicurarci la verità dei teoremi ma solamente quello di mostrarci come certi modi di ragionamento possono essere ridotti a modi più semplici.

Noi elencheremo solo pochissimi teoremi e non ne daremo le dimostrazioni; fatta eccezione per alcuni, giusto per mostrare come anche un computer li potrebbe fare.

Teoremi:

(T1) a . É . a

(T2) ab . É . a

(T3) ab . É . b

(T4) a ∩ a . = . a

(T5) a = b . = . (a É b) ∩ (b É a)

(T6) a É b ∩ c . = . (a É b) ∩ (a É c)

(T7)

(T8)

(T9)

(T10)

(T11)

(T12)

(T13)

(T14)

(T15) Ù . É . a

(T16)

(T17)

(T18)

(T19)

(T20)

(T21)

(T22)

(T23)

Diamo ora alcune dimostrazioni :

(T1) asserisce a É a . Partiamo dall’assioma (P11) che per D1. (con la sostituzione di “a” , ovunque compaia “b” ), si può scrivere a É a . = . aa = a ma aa = a è la formula (T10), valida nel sistema, che si dimostra, indipendentemente da (T1), a partire da (P1) che negata (per D3.) diventa giusto la (T10), se teniamo, anche, conto della (P4).

(T22) asserisce il sillogismo espresso in forma universale; le ipotesi del teorema sono:

(L1) a É b

(L2) b É c

per (P11), D1. e D2. diventano rispettivamente:

(L3) ab = a

(L4) bc = b

per D3. [operando con c∩ su (L1) e a∩ su (L2) ] e (T11), che si dimostra indipendentemente da (P6), si ottiene rispettivamente:

(L5) abc = ac

(L6) abc = ab

Da queste ultime per D2. si ha

(L7) ac = ab

e da questa per (L3) e D2. si ha

(L8) ac = a

che per (P11) e D1. si può scrivere

(L9) a É c

che è la tesi del teorema che si voleva dimostrare.

Per finire, diamo la dimostrazione di (T23), che è la stessa cosa di (C3), cioè il sillogismo in forma individuale.

Partiamo da (T22) e operiamo, per D1., le sostituzioni ι x ® a, a ® b, b ® c, ottenendo:

(ι x É a) ∩ (a É b) . É . (ι x É b)

per (C2) e D1. otteniamo la (T23).

NOTE

1. Per fare un esempio, sentiamo il giudizio che Benedetto Croce (a nostro parere, filosofo più che reazionario) dava sui logici matematici (tra i quali vi annoverava esplicitamente anche il Peano). Il Croce dice che costoro tentavano inutilmente di contrapporsi ai logici tradizionali (tra i quali, ovviamente reputiamo, egli si includesse) e pensavano di essere degli “innovatori”; in realtà, a suo giudizio, lo erano solo “per modo di dire, perché in effetto, come si è notato, sono ultrareazionari, cioè assai più formalisti del formalista Aristotele, scontenti delle divisioni poste da costui, non perché troppe e arbitrarie, ma perché troppo poche…” in B. Croce, Logica come scienza del concetto puro, Laterza, 1947, p. 387. TORNA
2. In latino l’aggettivo individuus veniva usato nel senso di indivisibile; sia concettualmente, cioè nel senso di pensato come indiviso, come noi lo useremo, sia fisicamente, come nel caso degli atomi democritei: “Ille atomos quas appellat id est corpora individua propter soliditatem…”, Cicerone, De Fin., 1 , 17. TORNA
3. Tanto più generale è una proprietà, tanti più individui essa comprende e tanto meno di altre proprietà vi sono incluse. Questa dualità inversa era già stata individuata da Leibniz: “Infatti, dicendo ogni uomo è animale, intendo dire che tutti gli uomini sono inclusi in tutti gli animali, ma intendo nello stesso tempo che l’idea di animale è compresa nell’idea di uomo. L’animale comprende più individui dell’uomo, ma l’uomo comprende più idee e forme; l’uno ha più esempi, l’altro più gradi della realtà, il primo ha più estensione, l’altro ha più intensione”, in Nuovi saggi sull’intelletto umano, IV, cap. 17, par. 8 riportato in Scritti filosofici di G. W. Leibniz, UTET, 1967, p. 627. TORNA
4. Il Peano, nel corso della sua opera di chiarificazione dei vari concetti della logica, ha usato diversi segni per esprimere l’idea elementare corrispondente al nostro “á” come: “K” e, in seguito, “Cls′”. TORNA
5. Relazione . = . ogni termine che collega due altri termini, come nei casi citati nel testo. Tale concetto potrà meglio essere precisato nel seguito. TORNA
6. Contributi notevoli alla realizzazione del sogno leibniziano, in particolare sul calcolo delle classi, erano stati apportati da Boole, Schröder, Peirce, ed altri. TORNA
7. Notiamo che Peano usava il termine “classe” come sinonimo di proprietà, di concetto, ecc. Ma successivamente (vedi PF) il termine “classe” è stato usato da tutti gli altri logici in senso estensionale, pervenendo a tutta una serie di paradossi irresolubili (a meno di non introdurre delle convenzioni più che arbitrarie). Perciò noi eviteremo accuratamente di usare i termini: “classe, insieme, aggregato” e simili al posto di proprietà per non cadere negli stessi errori dei logici moderni. TORNA
8. A proposito di scienza e e di metafisica sembra opportuno citare queste appropriate parole di F. Engels in Dialettica della natura, Ed. Riuniti, 1971, p. 221: “Gli scienziati credono di liberarsi dalla filosofia ignorandola o insultandola. Ma poiché senza pensiero non vanno avanti e per pensare hanno bisogno di determinazioni di pensiero e accolgono però queste categorie, senza accorgersene, dal senso comune delle così dette persone colte [osserviamo che a distanza di tempo da quando scriveva Engels, possiamo sostituire le “così dette persone colte” con “i così detti epistemologi”!] dominato dai residui di una filosofia da gran tempo tramontata, [ è molto ottimista Engels!] o da quel po’ di filosofia che hanno ascoltato obbligatoriamente all’Università (che è non solo frammentaria, ma un miscuglio delle concezioni di persone appartenenti alle più diverse, e spesso peggiori, scuole), o dalla lettura acritica e asistematica di scritti filosofici di ogni specie, non sono affatto meno schiavi della filosofia, ma lo sono il più delle volte purtroppo della peggiore; e quelli che insultano di più la filosofia sono schiavi proprio dei peggiori residui volgarizzati della peggiore filosofia …¶ Gli scienziati possono prendere l’atteggiamento che credono: essi sono sotto il dominio della filosofia. C’è da porre solo il problema se essi vogliono essere dominati da una cattiva filosofia corrente o da una forma di pensiero teorico che riposa sulla conoscenza della storia del pensiero e sui suoi risultati. ¶ Fisica, guardati dalla metafisica: è del tutto giusto, ma in un senso opposto. ¶ Gli scienziati fanno ancora condurre alla filosofia una vita stentata e puramente apparente, servendosi dei rifiuti della vecchia metafisica. ¶ Solo quando la scienza della natura e dalla storia avrà assorbito in sé la dialettica, tutto il ciarpame filosofico, esclusa la pura teoria del pensiero, diventerà superfluo, si risolverà nella scienza positiva. [Che per Engels, ovviamente, non coincide con il positivismo vecchio o nuovo che sia!]. TORNA
9. Operazione . = . manipolazione di segni tale che dati due segni che hanno una certa proprietà ne produce un terzo colla stessa proprietà; p.es. “ 1+2 = 3” o “a ´ b =c” sono operazioni dell’aritmetica; la prima tra termini, la seconda tra simboli. I termini della prima e i simboli della seconda denotano numeri, in questo caso. TORNA
10. I termini intensione, comprensione, estensione sono parte integrante del vocabolario della logica scolastica (intesa nel senso più lato); ma il loro significato ha sempre avuto le interpretazioni più varie da parte dei diversi autori e spesso anche da parte dello stesso autore da una frase all’altra (un piccolo campionario di questi vari significati si può trovare alle relative voci nel Dizionario critico di filosofia del Lalande). Noi abbiamo scelto, invece, di usarli dandone una definizione formale. Il Peano non usa tale terminologia. Solo in una nota della sua Logique Mathématique, OS-II, p. 259. (Qui e nel seguito indicheremo con i simboli OS-I, OS-II, OS-III i tre volumi di Opere Scelte di G. Peano, a cura di U. Cassina, Ed. Cremonese, Roma, 1958) introduce il segno “ext a” per indicare l’estensione della classe “a”, cioè l’aggregato di tutti gli individui “x” per cui si può asserire “xÎa” . Da tale nota si desume, se pur ve ne fosse bisogno dati i significati formali di tutta la sua opera, che (al contrario dell’uso oggi diventato universale in seguito al Russell) per lui una classe è nient’altro che una proprietà e quindi non è la stessa cosa della sua estensione (vedi PF). TORNA
11. Vedi A. Padoa, Logica, in Enciclopedia delle matematiche elementari e complementari, a cura di L. Berzolari, G. Vivanti, D. Gigli, Hoepli, 1979. – Osserviamo che la distinzione tra termini primitivi e termini derivati ha poco valore ma rende omaggio alla tradizione (vedi nota successiva). E’ un’illusione il pensare che il significato dei termini definiti si possa ricavare delle definizioni nominali; infatti, nessuno si sognerebbe mai di credere, che prendendo un complesso di segni a caso, anche se in ottemperanza alle regole formali, di avere inventato un nuovo concetto per il fatto che ha attribuito un nuovo nome a tale complesso di segni. Lo stesso dicasi per la distinzione tra definizioni ed assiomi. Tuttavia la distinzione tra gli assiomi ( includenti le definizioni) e i teoremi, anche se ha un valore solo relativo, è più importante in quanto stabilisce le condizioni necessarie e/o sufficienti per la validità di determinate asserzioni. TORNA
12. Ciò non significa che per far questo non sia necessario conoscere preventivamente i significati reali di essi; perché, nel metalinguaggio, per dare il significato reale di “” abbiamo dovuto conoscere quello delle particelle “e” e “non” che corrispondono ai segni “ ∩” e “~” rispettivamente. D’altra parte, noi possiamo stabilire una definizione nominale se e solo se conosciamo i significati sia del termine da definire che di quelli che lo definiscono (a meno che non si tratti di semplici abbreviazioni). TORNA
13. Nella (P10), a sinistra compare il simbolo “a”, che quindi non ha un significato definito, mentre a destra compare un termine con un significato ben preciso. Questo significa che l’assioma vale per qualunque significato di “a”. Cioè, è sempre vera la : “”, per qualunque “b”, anche se “b ¹ a”. Ne segue che la (P10) potrebbe prendersi come definizione di “Ù” anche se essa non ha la forma standard delle definizioni nominali che pretende la omogeneità dei simboli ai due lati dell’identità. Per questa ragione il Peano definisce la proprietà assurda con la formula “Ù = x ' (a Î Cls . É_a . x Î a)” cioè “Ù” significala proprietà che hanno tutti gli individui “x” di cui si può affermare che qualunque sia la proprietà “a” essi la posseggono. Con tale definizione risulta ovvio che tali individui dovrebbero avere anche la proprietà “ ã ” se hanno la proprietà “a”; ma dal momento che ciò è assurdo si deduce che non possono esistere individui con la proprietà “Ù”. TORNA
14. Di fatto il sistema deduttivo diventa, in questo caso, un’algebra di Boole. TORNA
15. Tale struttura viene detta un reticolo distributivo. La (P11) potrebe prendersi come definizione di “ É”. TORNA
16. Vedi l’Appendice e la Parentesi epistemologica. TORNA
17. M. Bunge, Scientific Research I, Springer-Verlag, 1967, p. 28. TORNA
18. M. Müller, The science of thought, London, 1887. Cit. In OS-II, p. 458. TORNA
19. In base a questa osservazione Peano ha speso gli ultimi anni della sua vita nel tentativo di fare accettare, almeno tra gli scienziati, un linguaggio universale. TORNA
20. Si vedano gli articoli su Archimede sul numero 4-5 di Mondotre. TORNA
21. Diogene Laerzio, Vite dei filosofi, p. 371, Laterza, 1976. TORNA
22. A causa di tale metafisica deteriore, oggi, è invalso l’uso di rovesciare il significato di modello che, una volta, rappresentava una idealizzazione della realtà, per cui è meno ricco di determinazioni rispetto ad essa; e, ora, invece, si usa per indicare una rappresentazione concreta di una struttura astratta la quale è necessariamente meno ricca del suo modello (?!). Oh, incoerenza del linguaggio empirista! Il modello diventa una copia imperfetta della realtà astratta! Siamo ritornati al peggiore platonismo, rivestito di spoglie empiriste! TORNA
23. Popper trascura l’aspetto statistico della falsificabilità, dando a quest’ultima un significato definitivo e discriminante, per cui, alla fine, non può tenere conto dell’effetto paradigma come giustamente gli fa notare Kuhn. L’aspetto teorico della realtà sensibile è correttamente individuato da Popper anche se, a nostro avviso, in maniera insufficiente. Si veda K. Popper, Congetture e confutazioni, Il Mulino, 1969, p. 112. Per la polemica Popper-Kuhn, si veda AA.VV., Critica e crescita della conoscenza, Feltrinelli, 1976. TORNA
24. Le stesse osservabili, di cui si abusa nel linguaggio della meccanica quantistica, non sono altro che astratti operatori nello spazio astratto di Hilbert ai quali, solo con un atto di una, a mio parere, deteriore metafisica, si attribuisce lo status epistemologico di rappresentare concreti atti di misura, impossibili ad attuarsi; per cui, alla fine, si ricorre alla, spesso utile ma non sempre necessaria, finzione degli esperimenti ideali. E qui ci sarebbe da chiedersi, a parte la loro utilità, perché un modello teorico si debba chiamare “esperimento”, sia pure ideale! TORNA
25. Con la sigla PR indicheremo l’opera: I Presocratici – Testimonianze e frammenti, Laterza, 1983 TORNA
26. Con la sigla DL indicheremo l’pera di cui a nota 21. TORNA
27. Tale divisione è una delle cause dei contrastanti giudizi che nel corso dei secoli sono stati dati sui Pitagorici, col confondere insieme le dottrine delle due correnti. TORNA
28. Riferisce Plutarco (PR p. 486): “Perciò appunto Platone mosse biasimo ad Archita e a Menecmo, che del raddoppiamento del solido cercavano di servirsi per costruire strumenti e meccanismi, sembrandogli che irrazionale fosse il loro sforzo pewr trovare, come potevano, due medie proporzionali; perché, diceva, in questo modo distruggevano e corrompevano quello che è il bene della geometria, riconducendola a cercare oggetti sensibili, e non mirando verso l’alto, per cogliere le immagini eterne e incorporee, presso le quali il dio essendo sempre è dio.” TORNA
29. “Infatti pare che Parmenide sia pervenuto all’unità secondo il logo, Melisso all’unità secondo la materia; perciò il primo dice che è finita, il secondo infinita.” Ed Elias (PR p. 288-89), parlando di Zenone, dice: “Al suo maestro Parmenide che diceva che l’essere è uno quanto al concetto e che invece quanto all’evidenza sensibile gli enti sono molti diede la sua adesione una volta, con quaranta argomentazioni nella tesi che uno è l’essere, ritenendo che fosse bello portare aiuto al suo maestro. Un’altra volta, appoggiando la tesi dello stesso maestro che l’essere è immobile, con cinque argomentazioni provò che l’essere è immobole. A questi argomenti non potendo Antistene il Cinico rispondere, si alzò in piedi e si mise a camminare, ritenendo che più sicura di ogni contestazione di ragionamenti fosse la dimostrazione mediante l’evidenza sensibile.” Quello di Antistene è il comportamento classico di ogni rozzo empirista. TORNA
30. Abbiamo aggiunto, in parentesi quadre, alcuni termini e modificato il genere dei relativi pronomi e aggettivi, senza di chè, a nostro giudizio, il testo della traduzione, da cui citiamo, risulterebbe privo di senso, anche grammaticalmente. TORNA
31. Apprendiamo, infatti da Filopono (PR p. 367-68): “E’ necessario, per Empedocle, ammettere che vi sono corpi solidi e indivisibili, dal momento che non vi sono in ogni parte del corpo pori contigui: e questo è appunto impossibile, perché altrimenti tutto il corpo sarebbe poro e vuoto. Cosicchè, se questo è impossibile, è necessario che le parti del corpo, che sono in contatto, siano solide e indivisibili, e vuote quelle intermedietra di esse, le quali Empedocle appunto chiama pori”. TORNA
32. Con numerabile è da intendere che all’estensione della proprietà “ente” si possa assegnare un numero intero (“tanti quanti sono”). Essendo che per il modo di pensare, riferito al concreto, degli Italici il numero, definito come corrispondenza tra insiemi, non avrebbe avuto molto senso, perché sarebbe stato giudicato un’illecita generalizzazione di proprietà che si possono verificare solo nel finito sensibile. Quindi per loro l’estensione dei numeri interi sarebbe “non numerabile” e quindi “infinita”, senz’altri aggettivi del tipo di quelli di Cantor. TORNA
33. Aristotele, Fisica, (208b 1-8), Laterza, 1973, p. 73. TORNA
34. Anzi sembra che attribuisse ai Pitagorici la conoscenza della legge di proporzionalità inversa al quadrato delle distanze (cfr. Pierre Thuillier, Isaac Newton, un alchimiste pas comme les autres, in La Recherche, n. 212, Juillet-Août, 1989.). Ringrazio il prof. Angelo Cunsolo per aver portato alla mia attenzione questo articolo. TORNA
35. B. Farrington, Scienza e politica nel mondo antico, Feltrinelli, 1960, p. 16: “… la colpa fu data al cristianesimo stesso; ma questa non è una soluzione, poiché, posto che il cristianesimo sia incompatibile con la scienza, rimarrebbe sempre da chiederci perché gli antichi abbandonarono la loro scienza per il cristianesimo. Anche le invasioni barbariche furono considerate causa della distruzione delle tradizioni di civiltà. Ma ciò solleva la grande questione delle cause per cui la parte civile del mondo perse la sua potenza e la parte incivile prevalse, e la sproporzione divenne così grande che i barbari sopraffecero l’Impero Romano. …Si è anche detto che la scienza greca decadde perché i romani non seppero assimilarla;…discutibile è il presupposto razzistico dell’attitudine scientifica dei greci…Dal punto di vista della razza, i pensatori greci erano elementi completamente misti. A quel tempo (come nel mondo moderno) molti dei più famosi scienziati “europei” avevano una buona dose di sangue orientale nelle loro vene; …se gli italiani moderni hanno molto contribuito alla scienza, mentre gli antichi romani hanno dato ad essa scarsissimi contributi, la spiegazione non va cercata nella razza. Viste insufficienti le cause esterne…si cercarono delle cause interne. Così è stato osservato molto giustamente che la base della scienza greca era troppo limitata. …i greci, pur avendo conseguito notevoli successi in matematica, fallirono nel campo della fisica. …Ma rimane da risolvere un’altra questione, quella delle cause per cui lo sviluppo della scienza greca si arrestò.” TORNA
36. Ibidem, p. 52. TORNA
37. O. Neugebauer, Le scienze esatte nell’Antichità, p. 46-47, Feltrinelli, 1974. TORNA
38. Cfr. S. Moscati, Le antiche civiltà semitiche, Feltrinelli, 1958. TORNA
39. Con la sigla FM indichiamo l’opera: G. Peano, Formulario Mathematico, a cura di U. Cassina, Edizioni Cremonese, Roma, 1960. TORNA