La Scienza e la Fede

Salvatore Notarrigo

Alle lezioni di catechismo, che regolarmente frequentai alla giusta età, avevo imparato che ad ogni bambino vengono assegnati, anche se invisibili, un angioletto e un diavoletto. L’uno tira il bambino verso il bene e l’altro, manco a dirlo, verso il male.

Non mi fu detto se tali esseri fossero presenti anche nell’età adulta. Naturalmente, allora, non mi son posto questo problema e, dal momento che non li ho mai visti, come San Tommaso, ho finito per non crederci più.

Ma ora, dopo tanti anni, mi è capitato di incontrare il mio diavolo. L’angelo, sfortunatamente, non l’ho ancora visto, però l’ha visto un inventore di cui vi dirò alla fine.

I1 diavolo mi si è presentato sotto le spoglie di Giuseppe Boscarino, il quale, con la sua passione per la filosofia della matematica, mi poneva difficili questioni sul concetto di numero, cercando di capire i moltissimi e non facili discorsi che Aristotele dedicò all’argomento.

Fin dalle elementari non avevo mai incontrato grossi problemi con la matematica, almeno per quella che normalmente si richiede ad uno studente, anche universitario; si trattava, quasi sempre, di risolvere ben determinati problemi, che come venivano posti mi parevano di una facilità estrema e non riuscivo a capire le difficoltà che incontravano molti compagni di scuola e colleghi di università.

Più tardi ho opinato che le difficoltà di costoro erano da connettere col fatto che essi si ostinavano a faticare per cercare di memorizzare il libro di testo, forse per quell’assurdo criterio pedagogico che, fin dalle scuole elementari, costringe i bambini a mandare a memoria delle poesie di cui non sempre ne è chiaro il senso; ma i significati, come è noto, a scuola contano poco, contano solo le parole, specialmente se sono belle, naturalmente, secondo il giudizio dei critici letterari — invece di limitarsi a intendere i significati delle definizioni a mezzo di opportuni modelli concreti, i quali, spesso, venivano forniti dal libro stesso e, altre volte, erano i nomi stessi a suggerirlo; del resto, anche il droghiere riesce a maneggiare pesi e misure, valutandone i reciproci rapporti di scambio senza, possibilmente, avere avuto necessità di andare a scuola o, il più spesso delle volte, avendo già dimenticato tutto quello che a suo tempo era riuscito a memorizzare al solo scopo di far contenta la maestra e i genitori.

Le definizioni e le ovvie regole del calcolo simbolico sono risultate, per lo più, sufficienti anche nella mia esperienza di ricercatore di fisica; finché non mi son messo in testa di capire i dettagli matematici delle teorie moderne della fisica, fondate sulle strutture della meccanica quantistica e della meccanica relativistica. Ma dopo un po’ ho capito che le mie difficoltà non dipendevano dalla matematica, ma dalla filosofia associata a tali teorie; per cui, ancora una volta, mi sono disinteressato dei problemi filosofici connessi con le teorie matematiche, in quanto tali, cioè astraendo dai loro possibili significati fisici.

Nei miei studi universitari, per sostenere gli esami ho dovuto, ovviamente, leggere il libro di testo, che era stato scritto dal titolare della cattedra del mio corso (per la cronaca dirò che il professore si chiamava Pia Nalli; ancora oggi giudico il suo libro un capolavoro!), e non ho avuto traumi, in quanto la filosofia, che vi intravedevo (anche se non esplicitamente espressa), non era in contrasto con il concetto che mi ero fatto della matematica, cioè di strumento essenziale per lo studio di problemi concreti (nel mio caso di fisica, principalmente).

Nel corso degli anni mi è capitato di leggere dei libri sulla filosofia della matematica; mi sono sempre risultati incomprensibili. Non essendo in grado di decidere se erano problemi seri o semplici giuochi di parole senza significato, mi riservavo, trovando il tempo, di studiare in seguito e più attentamente la cosa; ma, in ogni caso, giudicavo che i problemi, che in tali libri venivano sollevati, non dovevano essere molto rilevanti; infatti, non mi era mai capitato di imbattermi in tali sottili questioni, almeno nell’uso concreto che mi era capitato di fare della matematica.

In genere, nemmeno i matematici, con i quali mi capitava di chiacchierare su tali questioni, mostravano forti interessi sulla filosofia della loro scienza e, per quei pochi che ne parlavano, sembravami che avessero ricavato le loro idee, almeno quelle espresse, non già dal loro lavoro concreto ma dalle parole dei filosofi della matematica, i quali ultimi, con altissima probabilità, così almeno io giudicavo, non avevano mai fatto della matematica e tanto meno mi pareva che l’avessero mai applicata a un qualche caso concreto.

Strana situazione questa, mi dicevo, che i matematici debbano apprendere la filosofia della matematica da coloro che, spesso, non sanno che cosa la matematica sia. Ma oggi non capita solo ai matematici questo fatto singolare. Nè i fisici vi fanno eccezione.

C’è chi dice che la colpa sia da imputare alla soverchia specializzazione.

Ricordo un aforisma di Bernard Show che diceva che lo specialista è colui che sa tutto su nulla; ma, naturalmente, non è meno grave il sapere nulla su tutto.

Ad ogni modo, ho sempre pensato che anche l’imperativo della specializzazione deve pur avere la sua causa.

Ma ora sto cominciando a parlare come il diavolo! Mi piace dare la colpa a quel diavolo di cui vi ho parlato sopra; che, magari inconsapevolmente, mi ha spinto a riflettere sugli ardui problemi che prima avevo sempre rinviato.

Finalmente ho capito che tali astratti problemi di filosofia della matematica hanno un immensa rilevanza sulle teorie moderne della fisica; e non solo della fisica.

Ma andiamo con ordine.

Cosa sono i numeri?

Come si legge nell’articolo di Boscarino, in questo stesso numero di Mondotre, il problema è antico e sembra ancora non risolto.

Nascono i numeri dalle operazioni fisiche che compiamo per misurare una grandezza? O, non piuttosto, è il concetto di grandezza che sgorga dalle operazioni mentali che compiamo con i numeri? O, ancora, non potrebbe darsi che le due cose siano assolutamente separate, essendovi tra loro una semplice e casuale analogia formale?

Certo, dopo Cantor, l’analogia non può essere completa; noi mai possiamo operare fisicamente con grandezze transfinite; e dopo Robinson ancora peggio, visto che nessuno potrebbe mai operare concretamente con un infinitesimo attuale.

Non credo che a tali domande si possa dare una risposta definitiva se, preliminarmente, non si siano enunciati molto chiaramente gli assunti metafisici da cui si vuole partire.

Tuttavia si può, andando a ritroso, tentare di capire da quali assunti metafisici siano implicate le eventuali risposte alle dette domande e quali conseguenze logiche, a loro volta, implichino tali risposte.

Poi, ovviamente, ognuno sarà libero di scegliersi la propria metafisica, che più si concili con le personali esigenze; e sarà libero, anche, di scegliere sistemi metafisici autocontradittori; tanto i filosofi moderni della matematica, altrimenti chiamati metamatematici, hanno concluso che non è possibile dimostrare l’autocontraddittorietà di un sistema deduttivo.

È da lunga pezza che son finiti i bei tempi di Euclide e di Archimede! Oggi sono i tempi delle convergenze parallele. Alcuni hanno riso di questa frase pronunciata da un illustre uomo politico tragicamente scomparso, ma costoro, certamente, non avevano sentito parlare dell’esistenza delle geometrie non eucidee!

Fin da tempi preistorici gli uomini hanno misurato lunghezze, masse, aree, volumi, durate temporali, ecc., per cui è altamente probabile che i primi termini matematici coniati siano stati quelli corrispondenti ai concetti di “doppio” e di “metà” e quindi quelli più generali di “multiplo” e di “divisore”.

Con l’intensificarsi degli scambi dei prodotti del lavoro è probabile che abbiano sentito il bisogno di una qualche “unità di misura”, comune ad ogni singola specie di grandezza, con la quale erano soliti stimare le quantità dei beni prodotti; questo, appunto, può far nascere l’esigenza del termine collettivo “grandezza” e del concetto più specifico di “grandezze omogenee”, riferito alla sottoclasse delle grandezze direttamente confrontabili tra loro.

Le operazioni fisiche di confronto diretto tra una grandezza e l’unità ad essa omogenea sono certamente diverse, per le diverse grandezze; ma tutte hanno in comune qualcosa; e non certo perché tale qualcosa è immanente alle proprietà misurate, ma semplicemente perché, avendo misurato con successo una grandezza, supponiamo la lunghezza, si è cercato sempre di usare un metodo il più strettamente simile al primo, anche per le altre grandezze; anzi, nonostante lo sviluppo attuale degli strumenti di misura e della metrologia stessa, ancora oggi, si tenta sempre, non solo nei modelli teorici della teoria delle misurazioni ma anche nella realizzazione pratica degli strumenti di misura, di ricondurre ogni misurazione di una qualsiasi grandezza a una misura di lunghezza, come, p. es., lo spostamento di un indice su di una scala graduata. Solo negli ultimissimi tempi, con la diffusione dei calcolatori automatici digitali, si vanno sostituendo le scale graduate (compreso il quadrante dell’orologio da polso) con una rappresentazione visiva delle cifre arabiche in un opportuno quadro di lettura (display).

Sia con l’antica rappresentazione analogiea, effettuata mediante le scale graduate, sia, e a maggior ragione, con la rappresentazione digitale moderna, l’atto di misura di una qualsiasi grandezza viene ricondotto all’operazione di conteggio dei gradi della scala, che anche si possono leggere direttamente, senza bisogno di contarli, quando si sia provvista la scala graduata con delle cifre che ne riassumano il conteggio, il quale è stato già fatto, una volta per tutte, dal costruttore dello strumento con una più o meno alta approssimazione numerica; questa operazione, di riassunto e approssimazione, viene fatta automaticamente sulla mostra delle cifre nei dispositivi digitali di lettura (display).

Nell’uno, e ancor più nell’altro metodo di lettura, a lungo andare e con l’abitudine, si viene a perdere l’idea di grandezza come un continuo, il quale potrebbe, almeno in teoria, far assumere all’indice della scala una qualunque posizione, anche intermedia tra i gradi segnati, comunque fitta sia la graduazione stessa; e così, il numero viene ad assumere un esistenza propria, quasi come un personaggio pirandelliano che risulta essere più reale del carattere che vuole rappresentare; e viene anche l’idea che, se potessimo infittire a volontà la graduazione della scala (o, equivalentemente, il ntunero delle cifre nel display dei dispositivi digitali di lettura), potremmo far coincidere qualunque grandezza con un qualche segno della graduazione.

E ciò infatti, in pratica, si verifica sempre; ma solo perché non siamo in grado di distinguere due segni quando vengano a trovarsi sufficientemente vicini tra loro.

Ma già i pitagorici sapevano che ciò è, in generale, impossibile con esattezza assoluta; infatti, dimostravano che il lato e la diagonale di un quadrato sono “incommensurabili” in questo preciso senso, cioè: non possono esistere sulla scala due segni, che coincidano esattamente con gli estremi superiori delle due lunghezze, comunque si infittisca la graduazione; anche oltre il limite imposto dallo spessore, non mai nullo, del segno stesso e anche oltre i limiti impostici dal potere risolutivo finito del nostro occhio, pur provvisto di un potentissimo microscopio.

A un certo punto della storia del pensiero astratto il processo di “contare” viene ad apparire, quindi, come concettualmente antecedente a quello del “misurare”.

Il problema di sapere se, storicamente e concretamente, gli uomini abbiano imparato prima a contare e poi a misurare o viceversa, mi sembra un problema di inutile speculazione metafisica (nel significato deteriore del termine), anche se, dal punto di vista della “logica”, i due concetti, in quanto entità astratte, necessariamente, devono nascere insieme; e ciò proprio a causa della scoperta, di ordine logico, dovuta agli stessi pitagorici, secondo i quali, ogni qual volta si viene a formare un concetto, con lo stesso atto del pensiero, si forma contemporaneamente il suo contrario. Non può esistere, logicamente, il “continuo” senza il concetto di “discreto” e viceversa; nè tanto meno può esistere l’analogico senza il digitale e viceversa. E non ha alcun senso logico il tentare di costruire l’uno per mezzo dell’altro o viceversa.

Ma, in ogni caso, la questione sembra irrilevante per la scienza. Quello che conta è il sapere quale dei due concetti conviene prendere come mattone per costruire un sistema deduttivo, cioè quale usare come “termine primitivo”.

Gli antichi avevano deciso per il continuo e cioè per le grandezze.

I1 modello di grandezza di Euclide è un segmento di retta (che egli chiama “retta”, tout court, perché, probabilmente, gli sarebbe sembrato inconcepibile pensare a una retta indefinita, cioè senza limiti, o estremi che dir si voglia, anche se ogni “retta” può essere prolungata indefinitamente, senza con ciò cessare, ad ogni prolungamento, di restare limitata; quindi, per Euclide, è l’operazione del “prolungare” che può essere ripetuta indefinitamente e giammai, invece, la “retta” potrebbe essere infinita).

In tale segmento di retta si possono “segnare” dei punti in corrispondenza di ogni singola grandezza concreta, cioè individuale. Non a caso il punto, per Euclide, e anche secondo tutta la tradizione pitagorica, è σημεĩον, cioè “segno”.

Avendo segnato sulla retta dei punti equidistanti, la misura si riduce a un conteggio di segni. Tale conteggio può solo fornire un numero intero (un numero decimale è semplicemente un numero intero camuffato, cioè una particolare rappresentazione di un intero, quando si sia convenuto di usare la stessa unità di misura per tutte le singole grandezze della stessa specie, sia maggiori che minori dell’unità stessa).

Noi possiamo esprimere il risultato di una misura solo mediante un numero intero (possibilmente anche camuffato da razionale); ma un numero intero non esaurisce la totalità dei possibili confronti tra una qualsiasi grandezza e la sua unità, il confronto tra diagonale e lato del quadrato lo dimostra. Il rapporto tra grandezze (λόγος) è un concetto più generale di quello di numero, in quanto quest’ultimo rappresenta solo l’informazione, necessariamente approssimata, che possiamo “nominare”.

Ma il fatto che non possiamo nominare, per mezzo di una sequenza di cifre, un rapporto tra grandezze (come per esempio il rapporto tra la circonferenza e il suo raggio) non significa che non ne possiamo ragionare. Casualmente (o forse no!) il termine della lingua greca che esprime il concetto di “rapporto” è omonimo del termine che esprime il concetto di “ragione”.

E, perciò, risulta possibile ad Archimede inventare un sistema di numerazione che possa approssimare, con arbitraria (ma non infinita) precisione, un qualunque rapporto e, in particolare, quello che oggi indichiamo con il simbolo π ; o contare il numero dei granelli di sabbia che avrebbero potuto essere contenuti in un volume pari all’intero universo eliocentrico di Aristarco, ben noto allo stesso Archimede.

Con Dedekind, come leggiamo nell’articolo di Boscarino, vengono abolite le grandezze in favore dei numeri, e così nasce il falso problema di costruire il continuo mediante il discreto, risolto (a parole) con il “postulare l’esistenza” di un limite per ogni successione di razionali che costituisca una “sezione”; limite che, però, necessariamente, non sempre può far parte dei razionali, ammesso che questi ultimi possano avere un’“esistenza” propria in un qualche mondo iperuraneo. Con ciò i nomi ed i simboli diventano più importanti dei loro significati. Questo giustificherebbe il criterio pedagogico a cui abbiamo sopra accennato.

E, così, nei moderni libri di divulgazione della matematica si asserisce, con grande sicumera, che Euclide ed Archimede furono certamente dei grandi matematici, ma ... non seppero inventare i numeri reali! A sentire tali parole, i due grandi “scienziati” del nostro passato (e non semplicemente “matematici” o “geometri” o “fisici” o “ingegneri”, come spesso, facendo loro torto, vengono chiamati; infatti i due si sono entrambi occupati di tutte queste materie e non sarebbero stati in grado nemmeno di capire la distinzione!) si sarebbero messi a ridere dicendo: “Meno male! se l’avessimo fatto saremmo stati legittimati a sommare assieme un indice di rifrazione e un angolo poiché entrambi verrebbero ad essere numeri e i numeri, per definizione, si possono sommare. Ma noi non vogliamo sommarli perché non vogliamo commettere inutili sciocchezze! Per cui ci limitiamo a sommare solo le grandezze fisiche e giammai i loro rapporti”.

Ma che significa “esistere”?

Facilissimo! “esistere” significa “essere”. Sì d’accordo, ma che significa “essere”? Quando avremo esaurito i possibili sinonimi elencati nel dizionario ci ritroveremo ancora al punto di partenza.

Sembra ovvio che non si può definire tutto; anzi, per essere precisi, non si può definire niente, se con “definire” si voglia intendere l’acquistare il “significato” di un termine mediante il significato di altri termini, perché questo comporta un regresso all’infinito, come nel caso del termine “esistere” o, ancora peggio, per il significato di “significato”.

In logica e in matematica si danno delle definizioni, ma queste sono puramente “nominali”, cioè sono semplici convenzioni sul come operare con determinati nomi. Né con la logica, nè con la matematica, si possono acquistare “significati”; questi possono solo derivare dalle concrete operazioni che facciamo sulla realtà.

Nonostante ciò i filosofi della matematica si sono sempre sforzati di definire il numero; ma, naturalmente, la sola cosa che possono riuscire a fare è quella di descrivere, con parole più o meno proprie e più o meno significanti, il loro personale concetto, al quale sono portati a pensare quando odono la parola “numero”; concetto che loro deriva dalle personali esperienze, necessariamente sempre limitate, e che ardiscono, arbitrariamente, estendere urbi et orbi, fino a sistemarlo nel mondo iperuraneo, come già aveva fatto Platone.

Dopo Russell, il quale si è sforzato di mettere assieme le illusioni di Dedekind e di Cantor con l’ideografia di Peano, avendo il primo riconosciuto pubblicamente la lezione di quest’ultimo, in base alla quale non si può parlare di scienza senza un linguaggio adeguato e non ambiguo, si tenta di definire il numero, nominalmente, a partire dalla nozione di classe, ritenuta logicamente antecedente (sembra di essere tornati con questo linguaggio poco significante ad Aristotele!). La conclusione sarà che il numero è la classe di tutte le classi, che hanno lo stesso numero di elementi. Nel suo significato, tale definizione è patentemente circolare, anche se si può, con difficoltà e con qualche sotterfugio, metterla in simboli senza, apparentemente, ripetere due volte lo stesso simbolo, una prima volta, nel nome che si vuole definire e, una seconda volta, nella definizione stessa.

Mi sono dimenticato che stavamo parlando del termine “esistere”; ma la parentesi che abbiamo aperto non sarà inutile per meditare su alcuni possibili suoi significati.

Noi usiamo, spesso, il termine “esistere” per dire che, secondo la nostra opinione, qualcosa esiste nello spazio e nel tempo. In questo senso diciamo che esiste la terra ed esiste la luna. La terra la tocchiamo, la luna la vediamo e, oggi, sappiamo che qualche astronauta l’ha anche toccata. Ma, certamente, la terra che tocchiamo e la luna che vediamo non hanno forma sferica, al massimo la luna ha forma circolare piana, ma non sempre, qualche volta è falciforme.

Certamente non è questo il senso con cui la gente pensa che esistano i numeri.

Esistono forse allo stesso modo dei nostri sogni notturni o delle nostre fantasie diurne?

Nemmeno questo va bene!

Esistono come il fatidico uomo delle nevi o come la Cina di Marco Polo? Cioè, per sentito dire. No certamente!

Esistono come Dio o come gli angeli del paradiso in un mondo diverso dal nostro! cioè per fede. No! E allora?

Secondo me esistono in senso “logico”; come astrazione coerente dalle nostre operazioni fisiche concrete.

L’esistenza logica si può provare quando prima si siano introdotti dei simboli, si siano stabilite, convenzionalmente, le operazioni che possiamo fare con essi, e si sia riusciti a dimostrare che, nel nostro sistema deduttivo, l’esistenza di un qualche ente, definito nominalmente con i detti simboli, non risulti contraddittoria, in base alle convenzioni logico-linguistiche che abbiamo stabilito.

Possiamo dimostrare la non contraddittorietà del nostro sistema deduttivo? Certamente no! Questo lo sapevano, senza alcun dubbio, Euclide ed Archimede, e, probabilmente, anche i matematici Sumeri, e nessuno sentiva il bisogno del teorema di Gödel per saperlo, ammesso che tale teorema significhi qualcosa!

Noi possiamo, solamente, accertare empiricamente che i nostri assiomi e le nostre regole deduttive sono in accordo con qualche sistema concreto e funzionante.

Solo allora, l’esistenza logica, in qualche modo, diventa anche esistenza fisica; non nel senso di esistenza nello spazio e nel tempo o in qualche altro possibile mondo, ma nel senso che i nostri oggetti matematici corrispondono a precise e ripetibili operazioni fisiche, che possiamo effettivamente compiere sulla realtà e non solo sui simboli, i quali ultimi sono solo le larve delle cose. E queste ultime sono “cose” non perché le tocchiamo e le vediamo, ma perché le abbiamo ricostruito razionalmente nella nostra mente. Nessuno dubita oggi che la terra di forma quasi sferica che ruota intorno al sole sia più reale della terra che possiamo toccare e vedere. Ecco il significato del termine “scientifico”.

Scientifico non è il dato di fatto, ma è scientifica la spiegazione razionale del dato di fatto.

Ecco come, secondo me, esistono i numeri. Secondo questa definizione di esistenza, né i numeri di Dedekind, né a maggior ragione i numeri transfiniti di Cantor o quelli “non standard” di Robinson, possono esistere. E non solo perché non vi è nessuna operazione fisica che loro corrisponda ma perché (e proprio per la precedente ragione) non si può provare la loro coerenza sintattica, checché ne possano pensare i metamatematici.

I numeri di Euclide e di Archimede, invece, esistono perché si può verificarne, e lo facciamo tutti i giorni senza accorgercene, la loro conformità con le nostre più comuni operazioni fisiche, anche quando seguiamo le involuzioni delle spire di fumo della nostra sigaretta.

Pure gli animali, anche degli ordini più bassi delle classificazioni zoologiche, mostrano di saper contare e di saper stimare la misura di quelle grandezze che sono rilevanti per la conservazione dell’individuo e della specie, come diversi studi specifici hanno accertato.

Ci si potrebbe porre il problema di sapere qual è il minimo numero di termini che dobbiamo assumere come primitivi (oltre i termini della logica) e, quindi, non nominalmente definiti, per costruire l’intero sistema assiomatico relativo alle grandezze fisiche e ai loro rapporti (cioè quelli che oggi si chiamano numeri reali).

Si può dimostrare che basta un solo termine; e cioè quello di “equivalenza” in grandezza di due segmenti; il significato di tale termine viene “astratto” dalle nostre operazioni di “trasporto rigido” di un regolo fisico, che può essere un’asta di ferro o di legno o di plastica o di qualunque altro materiale, che noi giudichiamo come approssimativamente “rigido”.

Non è opportuno darne qui la dimostrazione, tanto più che la cosa è irrilevante per qualunque altra scienza, che non sia la filosofia della matematica.

Invece è molto più interessante considerare le conseguenze del concetto di numero astratto come emerso, attraverso posteriori riaggiustamenti, dalle idee dei vari Dedekind, Cantor, Russell e consoci metamatematici, sul piano della fisica e, perché no, anche dell’analisi economica.

Riprendiamo, per un momento, il concetto di asta rigida e seguiamo, per riassunto, il più fedele che ci riuscirà possibile, un dialogo tra un relativista convinto, un fisico sperimentale e un matematico puro (il dialogo fu scritto nel 1920)¹.

I1 dialogo si svolge, pressappoco, in questi termini: Il relativista chiede se ci siano ragioni, oggi, per ritenere vera la proposizione di Euclide, secondo la quale la somma di due lati di un triangolo è sempre maggiore del terzo lato.

I1 matematico si limita a dire che la verità della proposizione dipende dalla verità degli assiomi, sui quali non è competenza sua asserire alcunché.

I1 fisico si sorprende della risposta del matematico, in quanto i matematici hanno sempre asserito che gli assiomi della geometria sono autoevidenti. Ma il matematico gli risponde che, modernamente, non si pensa piu così.

Il fisico incalza: se il sistema è coerente non è evidente che la proposizione è vera? Ma il matematico dice che ci possono essere diversi sistemi tutti internamenti coerenti. La geometria di Lobačevskij ne è un esempio.

Tuttavia il fisico insiste che, sperimentalmente, la geometria euclidea è vera. Ma il relativista non è soddisfatto di tale affermazione e invita il fisico a descrivere dettagliatamente le operazioni che deve compiere per verificare la proposizione di Euclide di cui si stà discutendo.

Per il fisico la faccenda è molto semplice, dice: prendo dei regoli graduati e li misuro! Ma il relativista obietta: sembra che stiamo parlando di cose diverse, io sto parlando di geometria e, quindi, di spazio! non della materia! I tuoi esperimenti provano solo proposizioni intorno a quest’ultima.

Il fisico: ma io posso usare strumenti ottici.

Il relativista: peggio di peggio, ora tu parli delle proprietà della luce!

Il fisico: ora non capisco più di che cosa stai parlando se non mi permetti di fare alcuna misura! È il solo strumento a mia disposizione per sapere qualcosa sulla natura.

Il relativista misura i lati di un triangolo con un metro avvolgibile e trova che la proposizione di Euclide non è vera, e ne chiede il perché. Il fisico osserva che, quando il relativista misurò il terzo lato, allungò troppo il metro. Ma questi ribatte con sufficienza: perché non avrei dovuto farlo?

Risponde il fisico che egli è obbligato a misurare con un asta rigida, se vuole essere sicuro del risultato.

Ma cos’è un’asta rigida? chiede il relativista. Se noi abbiamo definito una misura di lunghezza mediante il confronto con un asta rigida come facciamo a verificare che l’asta di misura è rigida? Ci vorrà un’altra asta rigida e così via all’infinito. Tu mi fai ricordare, racconta il relativista, della storiella dell’orologio pubblico e del cannone. L’incaricato del cannone sparava regolandosi con l’orologio e l’incaricato dell’orologio, lo regolava con gli spari del cannone!

Ovviamente, continua il relativista, lo “standard” di lunghezza non può cambiare se cambiamo il materiale di cui è fatto!

A questo punto possiamo interrompere il dialogo in quanto, se accettiamo gli argomenti del relativista (ed io, personalmente, li accetto come logicamente incontrovertibili), dobbiamo concludere, in modo assolutamente logico e razionale, che non potremo mai accorgerci se l’unità di misura delle lunghezze (o, per questo argomento, di qualunque altra grandezza) si allunghi o si accorci per effetto del movimento, come nella teoria della relatività particolare, o di qualsiasi altra causa, come, p. es., l’ipotetico incurvamento dello spazio per effetto di campi gravitazionali, secondo la teoria della relatività generale di Einstein.

Ma, stranamente, il relativista di Eddington, alla fine del dialogo, concluderà esattamente all’opposto!

Questa conclusione, quando la lessi la prima volta, mi fece ricordare di quella storiella secondo la quale un giudice, il quale era soddisfattissimo delle lunghissime e molto pertinenti argomentazioni che aveva, con grande fatica, trascritto nella sentenza, la quale si concludeva con la frase di rito: “Per questi motivi l’imputato viene condannato”.

Ma, come qualche volta capita, motivi superiori, anche se estranei alla causa, hanno costretto il giudice a cambiare opinione sulla sorte dell’imputato. Tuttavia le argomentazioni della sentenza erano troppo belle e troppo ben connesse logicamente per essere modificate minimamente, quindi il giudice decide, non si sa se a malincuore, di modificare solo l’ultima parola: “Per questi motivi l’imputato viene assolto”.

Non diversamente fa il nostro relativista, e lo stesso fanno Einstein ed Infeld, infatti essi scrivono:² “L’esempio di cui stiamo per servirci è ancora più fantastico di quello dell’ascensore in caduta libera. Dobbiamo abbordare un nuovo problema: quello della connessione fra relatività generale e geometria. Cominceremo col descrivere un mondo nel quale abitano soltanto esseri bidimensionali e non più tridimensionali, come nel nostro mondo. I film ci hanno abituato a vedere degli esseri bidimensionali agire su schermi bidimensionali. Immaginiamo ora che quei fantasmi, vale a dire gli attori sullo schermo, esistano realmente, che essi abbiano la facoltà di pensare, che essi siano in grado di creare una scienza loro propria e che per essi lo schermo bidimensionale rappresenti lo spazio geometrico. Tali esseri sono incapaci di immaginare, in forma concreta, uno spazio a tre dimensioni, così come noi siamo incapaci di immaginare uno spazio a quattro dimensioni. Essi possono flettere e incurvare una linea retta, e sanno che cosa sia un cerchio, ma sono incapaci di costruire una sfera, poiché per ciò fare dovrebbero abbandonare il loro schermo a due dimensioni. In quanto a noi, siamo bensì capaci di torcere e curvare linee e superfici, ma non riusciamo a rappresentarci uno spazio tridimensionale torto e incurvato.

Supponiamo che qualcuno dal di fuori, vale a dire dalla «terza dimensione», tolga i nostri fantasmi dallo schermo e li trasferisca sulla superficie di una sfera di raggio immenso. Se i fantasmi fossero molto piccoli rispetto a tale superficie, se non disponessero di mezzi di comunicazione a distanza e se non potessero allontanarsi molto, essi non potrebbero accorgersi affatto del mutamento sopravvenuto. La somma degli angoli dei piccoli triangoli sarebbe sempre eguale a due retti. Per due piccoli cerchi concentrici il rapporto fra le circonferenze sarebbe sempre eguale a quello fra i raggi. Viaggiando in linea retta essi non farebbero mai ritorno al punto di partenza.

Ma supponiamo ... che inventino dei mezzi di comunicazione con i quali possano percorrere rapidamente distanze molto grandi. In tal caso essi costaterebbero che

andando dritto innanzi a loro, finirebbero per tornare al loro punto di partenza… che il rapporto tra le circonferenze non è eguale al rapporto fra i rispettivi raggi ... Essi cercherebbero probabilmente di imputare alla fisica le discrepanze osservate ... Ma presto o tardi scoprirebbero che c’è un modo molto più logico e convincente di spiegare i fatti ... Essi finirebbero per comprendere che malgrado la loro incampacità di rappresentarselo, il loro mondo è bensì una superficie a due dimensioni, ma sferica.”

Ma per gli argomenti del relativista di Eddington, anche se non per le sue conclusioni, gli esseri bidimensionali di Einstein e Infeld non potranno mai accorgersi di essere in uno spazio curvo, se il loro campione di lunghezza è immerso nello stesso spazio ed eseguano misure per confronto diretto. Essi non cambieranno la loro geometria ma chiameranno quadrati degli oggetti che gli esseri tridimensionali chiameranno quadrilateri non equiangoli in una superficie curva. Il relativista di Eddington, così come Einstein e Infeld, pensano che, per il fatto che abbiamo chiamato qualcosa “lunghezza”, essa sia perciò stesso una “grandezza” e non una semplice “quantità numerica”, infatti nelle geometrie non-eudidee si chiamano lunghezze certe funzioni numeriche degli angoli che, a loro volta, vengono definiti come semplici quantità numeriche e non come grandezze, si chiamano aree altre funzioni degli angoli, e così via. Le misure per confronto diretto non c’entrano per niente e non vengono menzionate.

Quindi qualunque fisica che si basi sugli spazi curvi non parla di grandezze fisiche, ma solo di numeri che non si sa come “misurare”, anche se si possono “determinare”, p.es., ponendo uguale a 1 l’angolo giro (definito come tutto il “piano” o, se si preferisce, lo “spazio bidimensionale anche curvo” che circonda un punto) e ponendo, per definizione, l’angolo retto uguale a 1/4. Certamente 1/4 rappresenta un numero, ma altrettanto certo è che “tutto” il piano non è una grandezza.³

Ma, allora, cos’è lo “spazio” e che sarà mai il “tempo”?

Non è peregrino leggere le seguenti parole di Peano: “In quasi tutti i trattati italiani moderni si introduce per primo il concetto di spazio, dicendo che esso non si definisce, ma gli si attribuiscono le proprietà di essere omogeneo, illimitato, infinito, divisibile, immobile, ecc., proprietà queste parimenti non definite. Ritenendo pertanto il concetto di spazio come fondamentale per la geometria, ne viene che non si potrebbe scrivere un trattato di questa scienza in una lingua che per avventura manchi di tali parole. Quindi non si potrebbe scrivere di Geometria nella lingua di Euclide e di Archimede, ove appunto manca la parola corrispondente al termine spazio, nel senso in cui lo si usa negli odierni trattati. In conseguenza una prima notevole semplificazione si ottiene col sopprimere puramente e semplicemente il termine spazio, gli aggettivi omogeneo, illimitato e tutti i postulati che legano quel soggetto con questi attributi. Questa osservazione sulla inutilità del termine spazio, in Geometria, riuscirà strana agli autori che incominciano il loro libro col parlare dello spazio. Però l’esempio di Euclide e di tanti altri che non ne parlano affatto, è del tutto convincente”.⁴

I “principi” organizzativi della geometria degli antichi erano il “punto” e la “distanza”.

Il primo veniva inteso come “segno” (σημεĩον) e, quindi, come “elemento” (στοιχεĩον) (= lettera con la quale comporre le altre parole). Dice Euclide che “il punto è ciò che non ha parti”, non nel senso che non ha estensione fisica (cosa che eventualmente deve risultare dagli altri assiomi che sono stati assunti in ogni specifico caso concreto) ma nel senso che non c’è nient’altro che possa essere considerato come una parte di un singolo punto, quindi: non sono le sue dimensioni fisiche che lo rendono “indivisibile” ma le sue proprietà logiche che lo fanno considerare come “atomo” del reticolo delle proprietà e, come diceva Democrito, potrebbe anche essere grande quanto il mondo. Si dice spesso che con Euclide viene introdotta la “geometria della precisione”, intendendo con ciò la possibilità di parlare di oggetti sensa dimensione fisica, ma questa, allora, sarebbe la geometria della confusione. La precisione di Euclide è di natura logica (come per Parmenide!) e il concetto di dimensione fisica è del tutto escluso dal concetto di punto.

Nella lingua comune il termine “punto” (come, del resto, ogni altro termine) viene usato in modo ambiguo, sia per parlare del singolo punto inteso come “individuo”, sia per indicare il concetto di punto che invece si riferisce a tutti i punti e non ad uno solo, cioè inteso come “proprietà” (e in questo senso, come notava il Peano, viene a coincidere con il concetto stesso di spazio), e ancora per parlare dell’“idea” di un singolo e determinato punto che, ovviamente, in quanto “idea” e altra cosa dal singolo punto pensato come “essere concreto” a cui l’“idea” si riferisce. Con l’ideografia di Peano è facile distinguere i tre concetti, ma entreremmo in un discorso troppo tecnico, non adeguato allo scopo di questo scritto.

La seconda (cioè la distanza) viene intesa, a sua volta, come il risultato di una ben precisa operazione fisica che trasporti rigidamente lungo una direzione la lunghezza di un segmento, pensato come l’insieme dei punti compresi tra i suoi due punti estremi. Ma cos’è mai un “trasporto rigido”? Oggi, come abbiamo visto, questo sembra essere un grosso problema. Noi ci accontenteremo di dire che è un’operazione fisica che lascia invariata la forma e l’estensione di un ente fisico come misurate dagli opportuni parametri: la lunghezza di una qualunque linea, l’area di una qualunque superficie, il volume di un qualunque corpo, gli angoli relativi tra i vari segmenti che possiamo individuare nel corpo; tutte grandezze queste che si suppone che abbiamo definito operativamente, altrimenti non potremmo chiamarle tali.

Oggi l’opinione generale è che gli antichi assumevano le proprietà del trasporto per “intuizione”; ma è più probabile, invece, che ne assumessero il concetto come una necessità logica conseguente al loro concetto di grandezza. Osserviamo che, a partire dai concetti di punto e distanza, si possono definire nominalmente (usando i soli segni della logica) tutti gli altri concetti della geometria come e stato mostrato da Peano e da Pieri.⁵

Già per i pitagorici (secondo la testimonianza di Aristotele) il punto si distingue dalla “monade unità elemento” in quanto oltre a essere una “monade” ha anche una “posizione” individuata da una terna di grandezze (“distanze”) relative ad altri punti dello spazio fisico, assunti convenzionalmente come punti di riferimento che necessariamente dobbiamo pensare come immoti ché il pensare che non lo siano sarebbe senza senso, non avendo alcun modo di accorgercene per l’assoluta omogeneità e isotropia del concetto di spazio (ovvero di “punto”) quando pensato come privo di ogni qualità particolare che può solo essere individuata quando, preliminarmente, si sia introdotto il concetto di materia (come, p. es., quello di essere spazio “pieno” di materia o spazio “vuoto”, cioè privo di materia) — e, pur avendo già introdotto il concetto di distanza e assunto come unità di misura la distanza tra due punti arbitrari, lo spazio resterebbe, di necessità, ancora “omogeneo e isotropo”, per la definizione stessa di grandezza; e una geometria cosiddetta “non-euclidea” (come geometria “fisica”) non sarebbe, “per necessità logica”, neppure pensabile in quanto questa impedirebbe qualsiasi trasporto rigido e, quindi, qualsiasi possibilità di confronto diretto.

Quindi, il punto che si considera in geometria, quando il termine “geometria” venga considerato nel suo significato etimologico, è rappresentato da una “tetrade”, cioè da una quaterna di punti (di cui tre di riferimento, in genere assunti tacitamente dal momento che poi si debbono considerare solo distanze relative) i quali insieme individuano una terna indipendente di dimensioni (cioè di distanze del punto considerato rispetto alla terna dei punti di riferimento); in geometria piana basta considerare una “triade”, cioè una terna di punti e una coppia di distanze; sulla retta (o, più in generale, su di una linea) il punto sarà una “diade” , cioè una coppia di punti (il punto in oggetto e quello di riferimento) e la distanza tra di essi.

Nello spazio fisico il numero di punti di riferimento necessario per individuare un punto qualsiasi mediante le sue distanze relative è, quindi, tre. Tali distanze vengono chiamate da Euclide rispettivamente: “lunghezza, larghezza, profondità”; infatti, per individuare il punto basterà pensarlo come uno dei vertici del tetraedo che ha come rimanenti vertici anche i tre punti di riferimento (riferimento comune a tutti gli altri punti dello spazio).

Nel libro primo, Euclide fa astrazione dalla terza dimensione e definisce la linea come lunghezza senza larghezza, restando implicita l’altra caratteristica di essere senza profondità, nel senso che, nel piano, il tetraedo può essere sostituito da un triangolo e, restando fissi i due vertici di riferimento, la linea può essere descritta facendo variare continuamente il terzo vertice con una legge determinata, di modo che su di essa abbia senso solo il concetto di lunghezza.

Nel linguaggio di Euclide, quando non è strettamente necessario, non si distingue tra la figura geometrica e la grandezza che gli compete e due figure sono per lui eguali se hanno la stessa estensione; ma, a differenza di quanto farà poi Archimede, la sua eguaglianza si limita alla coincidenza delle figure dopo un’operazione di trasporto fisico — traslazione o rotazione o riflessione — la quale, per definizione, mantiene invariate le distanze relative fra i punti della figura; invarianza che si suppone verificata per confronto con i due punti assunti come unità di misura delle distanze. Solo a poco a poco e costruttivamente, egli estende il concetto di uguaglianza anche a operazioni fisiche più complesse come quella del taglio ideale e ripetuto effettuato su di una figura con opportune rette (e nel libro undicesimo anche con piani) immaginando di poter sovrapporre le singole “parti” di una figura a quelle dell’altra per confrontarle.

Nell’asserire che gli estremi di una linea sono punti e che gli estremi di una superficie sono linee e che limite di un solido è una superficie, Euclide presuppone alcune fondamentali nozioni topologiche, molto probabilmente, già chiarite nella tradizione pitagorica.

Avendo introdotto la nozione di spazio come insieme di tutti i suoi punti, senza introdurre altre specificazioni, tale spazio coinciderà con l’“essere parmenideo” e cioè sarà: limitato, immobile, omogeneo, isotropo, e senza tempo. Avendo aggiunto la nozione di distanza tra punti se ne può rendere illimitata l’estensione, ma i suoi punti resteranno indifferenziati. Per differenziarli bisognerà aggiungere un’altra specificazione: la materia.

Per tali ragioni, secondo Newton, i punti possono essere materiali (punti di un solido ideale di densità massima “atomo democriteo”) e punti non materiali (punti dello spazio vuoto di materia). Un corpo fisico, nella sua apparenza, sarà una proporzione data di atomi e vuoto.

In geometria si astrae dalle proprietà particolari che tale mescolanza produce, basterà considerare la geometria degli atomi, cioè dei corpi solidi privi di “pori”, come già aveva precisato Empedocle, i quali, a loro volta, vengono “idealizzati” ulteriormente come figure geometriche con tre, due, una o zero dimensioni; basterà solo distinguere la figura dallo spazio vuoto; solo in esso è possibile effettuare traslazioni, rotazioni, riflessioni e separazioni arbitrarie.

Un punto materiale è interno alla figura, un punto del vuoto è esterno alla figura (la figura è un oggetto ideale e può essere semplicemente una periferia), i punti di contatto tra materia e vuoto sono “estremi” o “limiti” o “termini”.

A questo punto Euclide enuncia il suo concetto di “linea retta”, dicendo: Linea retta é quella in cui i suoi punti vi giacciono uniformemente (έξ ’ισου).

L’enunciato, in lingua greca, di questa asserzione ha sempre provocato grandi perplessità e, quindi, difformi traduzioni in base al suo dubbio significato. La mia ipotesi è che le perplessità derivano esclusivamente dal pregiudizio che Euclide non poteva possedere quelle conoscenze che solo dopo millenni sono state da noi moderni conquistate, dimenticando che il suo testo (seppure sia il suo o non piuttosto il suo completo rifacimento ad uso di leone d’Alessandria per i suoi studenti!) ci è pervenuto dopo secoli di quasi totale barbarie scientifica, malamente illuminato da vari commentatori medioevali che, a fatica, cercavano di risollevarsi alla luce della scienza, seppure ancor dentro il paradigma platonico-aristotelico.⁶

Credo che l’interpretazione più coerente e più nello spirito di tutta la scienza dei pitagorici si possa ricavare dall’impostazione della geometria come rigorosamente assiomatizzata dalla scuola di Peano (vedi nota⁵), come, del resto, lo stesso Pieri nota, riferendo la propria definizione di retta alle proposizioni XI e XII del terzo libro degli Elementi di Euclide, che ne costituiscono la proposizione inversa (nel piano).

Quindi la definizione euclidea si può rendere con: Dicesi retta quella linea in cui, presi due punti qualsiasi di essa, esiste sempre un punto in essa, e non più di uno, che ha la proprietà di essere equidistante dai primi due e non esiste alcun altro punto nello spazio che equidista dai due punti detti per lo stesso valore della distanza (probabilmente è questa proprietà di “equidistanza univoca” che Euclide vuole esprimere con il termine έξ ’ισου) o, equivalentemente: retta passante per due punti é il luogo dei punti di tangenza di due sfere che hanno per centri i due punti dati. Tale definizione è equivalente a quella successivamente data da Archimede come linea di lunghezza minima (oggi detta “geodetica”). Notiamo che, avendo assegnato le precedenti proprietà, non si definisce univocamente una retta, ma se ne ne dà solo una delle sue proprietà; infatti, qualunque geodetica, in una varietà riemanniana comunque curva, soddisfa le precedenti definizioni.

Subito dopo, Euclide definisce l’angolo piano come la pendenza relativa (κλίσις) di due linee in un piano che si incontrino tra loro ma che non giacciano su di una linea retta.

Molti commentatori, all’interno del paradigma hilbertiano, trovano tale definizione circolare in quanto si definisce l’angolo mediante il termine pendenza che si può definire solo mediante la nozione di angolo.

Ma è proprio vero questo? Forse tali commentatori dimenticano che per Euclide la pendenza (così come la distanza e l’angolo) è una grandezza fisica e non un semplice numero, come per Lobačevskij, o un nome senza significato, come per Hilbert! E qualunque agrimensore, fin da tempi molto più remoti, sapeva come misurare una pendenza per confronto con un’unità di misura assegnata. Quindi Euclide si limita a dire che l’angolo è la stessa cosa di una pendenza, solo misurata in una scala diversa, additiva per le aree.

Infatti, il fatto che Euclide definisce l’angolo per due linee in generale, e non per due rette, porta a pensare che l’unità di misura degli angoli piani doveva essere un’area, per cui la pendenza poteva ben essere individuata dal rapporto tra la “misura” dell’area compresa tra le due linee date e la circonferenza di un cerchio, di raggio opportunamente determinato (a seconda del caso concreto in esame, ma sempre con centro nel punto di incontro tra le due linee) e la “misura” dell’area del cerchio stesso. Ovviamente, solo quando le due linee fossero state delle rette si sarebbe potuto dare una regola generale per tale misura; potendosi, in questo caso, scegliere un cerchio di raggio qualunque; per cui, nei suoi “Elementi”, Euclide si limita nel seguito a trattare solo degli angoli rettilinei.

Un tale rapporto può essere dato, in tutta generalità, con i metodi di Archimede che, per la prima volta, fornisce il modo di misurare il rapporto tra l’area del cerchio e il quadrato del suo raggio. Ma, per le dimostrazioni di Euclide, non è necessario conoscere tale numero, bastando solo assumerne l’esistenza.

Senza un criterio di misurazione per gli angoli non si potrebbero definire gli angoli retti come quegli angoli adiacenti “uguali” formati da due rette intersecantesi; ché, se si volessero definire gli angoli come porzioni di piano limitate da due raggi, come in epoche posteriori si è cominciato a fare, non si potrebbe misurare il rapporto tra due grandezze (ammesso che lo siano!) che si sa dove cominciano e non si sa dove finiscono!

Per angoli rettilinei è possibile farlo purché si ammetta l’indipendenza della “misura” dell’angolo dalla lunghezza del lato, a ciò provvede Euclide enunciando un assioma in cui si asserisce che tutti gli angoli retti sono uguali tra loro. E poiché per Euclide “uguale” (ǐσος) significa eguale in grandezza, ne viene che se si assume tale assioma non e possibile nessuna geometria che non sia euclidea come molti matematici del passato hanno dimostrato; in questo specifico contesto bisogna ricordare il Wallis (1616 - 1703) e il Saccheri (1667 - 1733)⁷.

Ma, allora, qual è il significato fisico delle cosiddette geometrie non-euclidee, delle quali si è fatto un gran parlare tra matematici e fisici, e di cui ancora si parla, specialmente da parte dei volgarizzatori scientifici?

Poiché sovente si leggono affermazioni piuttosto strane, secondo le quali da una parte la possibilità di tali geometrie verrebbe provata empiricamente dalla teoria della relatività e, a sua volta, la teoria della relatività riceve l’avallo dalla coerenza delle geometrie non-euclidee, chiudendo così un circolo vizioso, sarà bene esaminare la questione un pò più a fondo.

Ci sarebbe, intanto, una questione che potrebbe apparire puramente nominalistica se non si collegasse direttamente alla nuova metafisica sulla funzione della scienza. Scriveva, p. es., Peano:⁸ “Certo è permesso a chiunque di premettere quelle ipotesi che vuole, e lo sviluppare le conseguenze logiche contenute in quelle ipotesi. Ma affinché questo lavoro meriti il nome di Geometria, bisogna che quelle ipotesi o postulati esprimano il risultato delle osservazioni più semplici ed elementari delle figure fisiche. La Geometria di posizione, o proiettiva, poi, è una parte della Geometria generale; quindi i suoi postulati si debbono trovare fra quelli assunti per la Geometria generale.

In conseguenza, sotto il punto di vista pratico, non parmi lecito l’assumere ad es. come postulato su cui fondare la Geometria proiettiva il seguente:

«Due rette giacenti in uno stesso piano hanno sempre un punto in comune», poiché questa proposizione non si verifica con l’osservazione, ed è anzi in contraddizione coi teoremi di Euclide.

La Geometria proiettiva parte dai postulati della Geometria elementare, e, con opportune definizioni, introduce nuovi enti, detti punti ideali (sia nella Geometria Euclidea, che nella non Euclidea), e ne risulta così che i nuovi enti ottenuti soddisfano alle proposizioni precedenti”.

Il fatto paradossale è che i primi autori che si sono occupati di geometrie non-euclidee partivano dall’esigenza di far ritornare lo studio della geometria, che era ormai diventato troppo astratto, all’antico legame con le “operazioni fisiche”; ma quando, dopo i primi rifiuti da parte dell’“Accademia” di accettare come scientifiche le proposte di tali innovatori (come sempre naturalmente accade), si è acceso il fervore per tali nuove geometrie, tali esigenze furono completamente dimenticate e l’avvento della relatività, nonostante le analisi operativistiche dei primi lavori di Einstein (come esamineremo in seguito parlando più specificamente di tale teoria), non ha modificato l’atteggiamento astratto dei geometri, atteggiamento che, invece, si è imposto anche tra i fisici.

Scriveva Lobačevskij:⁹ “Tutta la matematica è scienza della misura; tutto ciò che esiste nella natura, è assoggettato alla condizione necessaria di essere misurabile: perciò la differenza tra grandezze deve ricondursi a un diverso genere di misura e ai numeri che rappresentano le loro misure; tutti gli altri concetti saranno sempre oscuri e insufficienti” .

Sembra lo stesso linguaggio di Newton, ma non è così! perché, quando Newton parla di misure vere e matematiche intende quelle “assolute”, mentre Lobačevskij si riferisce a quelle sensibili che per Newton sono “relative”, apparenti e volgari.

Infatti, precisa Lobačevskij:¹⁰ “Nella natura noi abbiamo cognizione, propriamente, soltanto del movimento, senza il quale le impressioni sensoriali sono impossibili. Pertanto tutti i rimanenti concetti, per esempio quelli geometrici, sono creazioni artificiali della nostra mente, tratte dalle proprietà del movimento; ecco perché lo spazio, in sé, separatamente preso, per noi non esiste. Dopo di che nella nostra mente non vi può essere nessuna contraddizione, se supponiamo che talune forze della natura seguono una geometria, altre un’altra loro particolare geometria. Per chiarire questo pensiero supponiamo (e di ciò molti sono convinti) che le forze attrattive si indeboliscano per la diffusione della loro azione su superfici sferiche. Nella Geometria ordinaria si prende la grandezza uguale a 4πr² in corrispopdenza del raggio r, dal che si ha che la forza deve diminuire proporzionalmente al quadrato della distanza. Nella Geometria immaginaria¹¹ io ho trovato che la superficie della sfera è:

π (e ^r- e ^{- r}) ²

e può essere che tale geometria seguano le forze molecolari, ogni particolarità delle quali dipenderebbe con ciò dal numero ‘e’, sempre molto grande. Del resto, sia dato questo esempio come pura ipotesi, a conferma, della quale è necessario trovare altre più convincenti prove. Di una cosa tuttavia non è permesso di dubitare: che le forze da sole generano tutto: movimento, velocità, tempo, massa, perfino distanze e angoli. Con le forze, tutto si trova in stretto legame: non riuscendo a cogliere l’essenza di tale legame, non possiamo affermare se nelle relazioni di grandezze eterogenee tra di loro debbono intervenire soltanto i loro rapporti. Ammettendo la dipendenza dal rapporto, perché non supporre anche la dipendenza senz’altro? Alcuni casi parlano già in favore di questa opinione: la grandezza della forza di attrazione, ad esempio, si esprime con la massa, divisa per il quadrato della distanza. Per distanza uguale a zero, questa espressione, propriamente, non rappresenta nulla. È necessario cominciare con una distanza purchessia, grande o piccola, ma sempre effettiva, e solo allora la forza compare. Ora si chiede: la distanza come mai genera questa forza? come mai sussiste nella natura questo legame tra oggetti così eterogenei? Non riusciremo probabilmente mai a pervenire a ciò; ma quando è vero che le forze dipendono dalle distanze, allora i segmenti possono del pari essere dipendenti dagli angoli”.

Il “matematico” Lobačevskij vuole ridurre tutto a forze, il “fisico” Hertz, al contrario, vuole eliminare le forze dalla fisica!¹²

Ma vediamo di capire meglio il significato di grandezze omogenee ed eterogenee a cui si riferisce il Lobačevskij.

L’espressione x = α u definisce una grandezza omogenea in rapporto alla sua unità di misura. Più in generale, se conveniamo di indicare con Q_a la classe di tutti i termini α a, in cui α Î Q è una quantità (= valore = misura = numero) e a è una grandezza determinata allora, per definizione, Q_a esprime la classe di tutte le grandezze omogenee con a. Se b Ï Q_a e b Î G (cioè: b è una grandezza) allora a e b sono grandezze eterogenee.

Non sempre è definita la somma di due grandezze omogenee (p. es. non ha senso, in generale, la somma di due densità, a volte scriviamo ρ = ρ₁ + ρ₂ come abbreviazione di sotto la condizione “ineliminabile” che v deve essere uguale in tutti e tre i membri, in quanto, in effetti, si sommano le masse e non le densità.

Se è definita “operativamente” la somma, si parla di “grandezza estensiva”; nel caso che non lo sia e, però, la grandezza sia definita come il rapporto di due grandezze estensive, si parla di “grandezza intensiva” (tale vocabolario si ricollega alla distinzione newtoniania tra “extensio” ed “intensio” ed è usuale nell’odierna termodinamica teorica).¹³

In tal caso la somma non è definita (e non può essere definita!), semplicemente perché non avrebbe alcun senso la somma tra grandezze eterogenee (tuttavia nei libri di meccanica statistica moderni si sommano tranquillamente impulsi e coordinate!).

Il risultato del prodotto di due grandezze omogenee (quando ha fisicamente senso) è una grandezza eterogenea alle prime due (p. es., l’“area” del quadrato non è omogenea con la “lunghezza” del suo lato).

Il prodotto di due grandezze eterogenee (quando ha fisicamente senso) è una grandezza eterogenea alle due di cui si è fatto il prodotto.

In fisica risulta opportuno, più generalmente, introdurre grandezze come funzioni di altre grandezze (p. es. ).

In tal caso si deve pretendere che la funzione matematica che definisce la nuova grandezza debba essere non omogenea nella grandezza che si definisce e che, invece, sia omogenea nell’eguaglianza che esprime una legge fisica.

Citiamo da Peano:¹⁴

“Le aree costituiscono una classe di grandezze indipendenti dalle lunghezze. Da Herone in poi si fa la convenzione:

Quadrato di lato 1 = 1

cioè si identifica Cq = C² ; o, in altre parole, si fa la convenzione:

Rettangolo di lati a e b = a ´ b.

Parimenti, senza alcuna convenzione, si ha:

Parallepipedo ortogonale di lati a, b, c = (cubo dilato 1) ´ a ´ b ´ c;

e si suol fare generalmente:

Cubo di lato 1 = 1.

Si potrebbe fare una convenzione diversa, ponendo p. es.:

Cerchio di raggio 1 = 1.

Gli angoli piani si sogliono misurare col retto, col grado sessagesimale = retto/90, col centesimale = retto/100, col mill = retto/16000; e infine col radiante, o angolo chiuso dall’arco eguale al raggio, = retto ´ (2π).

In geometria e in fisica si fa spesso

Radiante = 1,

e si identificano gli angoli ai numeri astratti. Però questa convenzione è meno frequente delle precedenti; ed è più pericolosa…

Una legge naturale, fisica o economica, si suole esprimere coll’eguaglianza di due funzioni di certe grandezze. Dividendo l’un membro per l’altro, essa potrà assumere la forma:

funzione di alcune grandezze = 1.

Per funzione non si deve intendere solo una funzione analitica, ma un’espressione composta col linguaggio ordinario. Ad esempio, il rapporto fra la lira e il franco è una funzione del tempo, che, pel tempo passato risulta dai listini di borsa, e pel futuro risulterà quando sia passato. Nessuno pensa di trovarne l’espressione analitica.

Si dice che la legge è omogenea rispetto a una grandezza C quando, ridotto il secondo membro=1, il primo membro è funzione omogenea di grado 0 di C, cioè non dipende da C; o, sotto forma volgare, non varia se al posto di C metto 2C.

Se la relazione non è omogenea in C, da essa si può ricavare C, cioè può servire a definire la grandezza C.

Perciò le definizioni delle grandezze fisiche non sono omogenee nella grandezza che si definisce.

Centimetro = 10^-9 ´ quadrante terrestre,

«Gramme=poids absolu d’un volume d’eau pure égal au cube de la centième partie du mètre, à la température de la glace fondant», come dice la legge del 18 germinale anno III (7 aprile 1795), non sussistono se al posto di C metto 2C.

In geometria pura ogni relazione fra lunghezze è omogenea. Se una lunghezza è funzione di altra lunghezza definita colla sola geometria senza introdurre altre lunghezze, quella funzione è una proporzionalità. Quindi per definire una lunghezza assoluta, il c, bisogna parlare di meridiano terrestre o di anno luce, uscendo dalla geometria pura.

Se si nega il postulato delle parallele, allora da un punto si possono condurre due parallele ad una retta che formano un angolo, funzione delle distanze del punto dalla retta. Questa relazione non è omogenea; quindi posso determinare una lunghezza assoluta, che chiamasi raggio di curvatura dello spazio. Alcuni preferiscono dire che anche le formule di pangeometria¹⁵ sono omogenee, purché si introduca il raggio di curvatura.

Gli antichi Cinesi si rappresentavano, come tutti i popoli primitivi, la terra piana; osservarono che camminando verso il nord, l’altezza del polo sull’orizzonte aumentava. Considerarono il rapporto fra il cammino e l’incremento di quest’angolo; ed ottennero una lunghezza assoluta, che chiamarono diametro del mondo. Noi lo chiamiamo raggio terrestre.

Nei trattati di meccanica e di fisica si dimostra la formula che dà la durata di oscillazione di un pendolo, come segue.

Se la durata, cioè un a quantità di s, è funzione della lunghezza del pendolo= quantità di c, e della gravità=quantità di cs^-2, e se questa relazione è omogenea, si potranno determinare i numeri p e q in modo che:

,

da cui p + q=0, -2q = 1, onde p = 1/2, q = -1/2 , e

durata = coefficiente ´ .

Ma molti autori sopprimono 1’ipotesi che la formula debba essere omogenea.

Per rendere evidente questa illusione, prodotta dalla confusione fra grandezze e numeri, considero, per esempio, la distanza r dalla terra al sole, che è una funzione del tempo t. Per trovare la natura di questa funzione poniamo r = f(t); cambiamo l’unità di tempo, prendendone un’altra k volte più piccola; allora la nuova misura del tempo sarà kt; ma r deve restare immutato; dunque dovrà essere f(kt)=f(t),

cioè f(t) è costante, e la distanza dalla terra al sole è costante; parimenti costanti sono le reciproche distanze di tutti i corpi celesti e terrestri!…

Se una legge fisica stabilisce una relazione fra grandezze di specie diversa, e questa non è omogenea, si può ricavare una di queste in funzione delle altre.

O altrimenti, se nell’enunciato della legge fisica si sono indicate tutte le grandezze che vi compaiono esplicitamente e implicitamente in guisa che nessuna grandezza non indicata esplicitamente si possa ricavare da quella relazione, allora essa è omogenea”.

Se accettiamo le “convenzioni” di cui sopra, e notiamo che tali convenzioni sono state sempre fatte, consciamente o inconsciamente, fin dall’antichità (chi ha deviato l’ha sempre fatto inconsciamente, non avendo mai fatto una misura diversa da quella che si può compiere guardando le lancette sul quadrante di un orologio o esperienze similari)¹⁶ che cosa possiamo dedurre intorno alla formula di Lobačevskij che esprime la superficie della sfera nella sua geometria? e che cosa dobbiamo pensare della sua tesi secondo la quale “non possiamo affermare se nelle relazioni di grandezze eterogenee tra di loro debbono intervenire soltanto i loro rapporti”? E che cosa, ancora, della sua proposta che “Ammettendo la dipendenza dal rapporto, perché non supporre anche la dipendenza senz’altro?” O, più in generale, qual è la rilevanza fisica delle geometrie non-eucidee?

Per rispondere alle prime tre domande basta ricordare che la dipendenza dai soli rapporti (e quindi l’“omogeneità”) si pretende solo per le leggi fisiche; mentre, al contrario, per le definizioni di una grandezza come funzione di altre grandezze si pretende l’“eterogeneità”. Quindi la formula di Lobačevskij, essendo eterogenea, si deve intendere come definizione di superficie della sfera. Ora è chiaro che ognuno è libero di definire tutte le grandezze che vuole, a seconda dei suoi scopi; ma, generalmente, non è ritenuto conveniente, se si vogliono evitare confusioni e slittamenti semantici, il chiamare la nuova grandezza con un nome che, fin dall’antichità, è stato usato per un’altra e diversa grandezza, con la quale, tuttavia, è obbligatorio stabilire le derivanti connessioni.

Una grandezza fisica può essere definita operativamente sia per confronto diretto con la sua unità di misura, o in modo indiretto mediante un’equazione tra grandezze. Questo, naturalmente, vale anche per l’area di qualche superficie. L’area si può definire (cfr. Perucca) in modo diretto mediante un’operazione fisica che può essere effettuata, p. es., mediante un planimetro; o, come è più usuale, dal confronto con un quadrato di lato l, mediante l’equazione definitoria S = l² . In quest’ultimo caso la superficie sferica vale sempre (come legge fisica e quindi “omogenea”): S_sfera = 4πr², dal momento che la geometria non può cambiare, per se stessa (cioè senza esplicite convenzioni sul tipo di misure che dobbiamo fare), il risultato di una misura.

Sulla base di tale confusione linguistica, assunta a postulato metafisico, lo stesso Lobačevskij (usando misurazioni astronomiche) e anche Gauss (usando misurazioni geodetiche) tentarono la verifica empirica della “verità” della geometria euclidea! Alla luce delle infinite (e spesso contraddittorie) riflessioni epistemologiche prodottesi in seguito alla teoria della relatività, tali tentativi appaiono, perlomeno, ingenui.

Per cercare di capire questo fatto, rispondendo così all’ultima domanda che ci siamo posti, è utile riportare un classico esempio, dovuto a Bridgman¹⁷ che mostra, in modo inequivocabile, come la diversa definizione operativa di una quantità fisica che, intuitivarnente, dovrebbe dare lo stesso risultato, ci costringe a concludere che due metodi diversi di effettuare una misura non necessariamente misurano la stessa grandezza fisica. Tale identità può solo essere affermata, con un grado maggiore o minore di certezza, solo dopo un’accurata analisi teorica e sperimentale: “Il concetto di velocità, come definito di solito, implica i due concetti di spazio e tempo. Le operazioni con cui noi misuriamo la velocità di un oggetto sono queste: dapprima osserviamo l’istante in cui l’oggetto è in una posizione, poi osserviamo l’istante in cui esso si trova in un’altra posizione, dividiamo la distanza fra le due posizioni per l’intervallo di tempo e se necessario, quando la velocità è variabile passiamo al limite.

Questo concetto di velocità, così definito, può venir usato come strumento per descrivere la natura e si troverà che la natura ha certe proprietà: per esempio, la velocità della luce è 3. 10¹⁰ cm/s. Inoltre a nessun oggetto materiale può venir impressa una velocità altrettanto elevata; all’aumentare della sua velocità verso questo valore, occorrono incrementi di energia crescenti senza limite.

Vi è ancora un altro modo assai interessante di definire la velocità, in cui non si compie affatto l’analisi in termini di spazio e tempo, bensì la velocità viene misurata direttamente ricostruendo la velocità data mediante l’addizione fisica di una unità di velocità scelta arbitrariamente. ... Noi possiamo anzitutto costruire un campione concreto di velocità, per esempio stendendo un filo tra due sostegni con un peso fisso per tenerlo in tensione. Se urtiamo il filo, lungo di esso si propaga un disturbo che possiamo seguire con l’occhio; definiamo unità di velocità la velocità di questo disturbo. Un oggetto ha una velocità maggiore dell’unità se precede il disturbo, minore se rimane indietro. Possiamo ora duplicare il nostro campione, costruendo un altro sistema di sostegni con filo teso, e controllare l’eguaglianza delle due velocità osservando se i due disturbi procedono insieme. Definiamo due unità di velocità di qualcosa che corra insieme col disturbo del filo del secondo sistema, quando il secondo sistema si muove con una velocità tale che esso corre insieme al disturbo del primo filo. Si può estendere indefinitamente il processo, e misurare qualunque velocità.

…si trova che la velocità della luce è infinita. Inoltre, non vi sarebbe alcun limite alla velocità che si può impartire ai corpi materiali dando ad essi un’energia illimitata, cosa che l’esperienza ordinaria ci ha preparato a considerare come semplice e naturale. La velocità infinita della luce, d’altra parte è quanto mai innaturale, specialmente se noi ci atteniamo al punto di vista del mezzo di trasmissione.”

Da questo esempio ricaviamo l’esigenza di analizzare le operazioni fisiche che effettivamente compiamo prima di dedurre qualcosa su di una qualunque grandezza fisica, anche in riguardo a quei concetti che da tutti sono ritenuti più semplici e primordiali, come quelli di spazio, di tempo e di movimento.

Era questa, del resto, l’esigenza che aveva avanzato Einstein nel suo famosissimo lavoro in cui sono state gettate le basi della relatività.

In passato era difficile trovare un libro di testo di Fisica, o di Meccanica Razionale, o di Geometria (e persino molti libri di Analisi Matematica) che non cominciasse con una trattazione delle grandezze fisiche. Oggi la teoria delle grandezze è scomparsa persino dai libri di Fisica; qualcuno vi dedica due o tre paginette che, senza accorgersene, contraddirà nelle pagine successive.

Ma, per parlare di relatività, è bene chiarire il significato di “spazio assoluto” e “tempo assoluto”, anche perché con gli stessi nomi, spesso, nella letteratura si intendono cose assolutamente diverse, provocando non pochi fraintendimenti.

Alcuni autori, senza darne un’esplicita definizione, sembrano contrappore l’aggettivo “assoluto” a “relativo” inteso quest’ultimo nel senso che noi possiamo misurare solo differenze di coordinate (siano esse spaziali o temporali). Ma questa distinzione è troppo banale per avere una qualche rilevanza fisica o filosofica in quanto l’affermazione della relatività (intesa in questo senso) ci dice solo che noi possiamo scegliere ad arbitrio l’origine delle coordinate. Ma questo era un fatto ovvio sia per Galilei che per Newton (anche se non lo era nella fisica aristotelica).

Per Newton i due termini facevano riferimento: l’uno (l’assoluto) a una pura convenzione “logica” e perciò insopprimibile in quanto distinzione puramente logica tra lo spazio e il tempo (proprietà distinte da qualunque altra proprietà esprimibile con parole), l’altro (il relativo) alle “concrete misure sensibili” che noi possiamo compiere; le quali ultime, naturalmente, sono affette da errori sia sistematici, sia casuali, sia dovuti alla sensibilità finita dei nostri strumenti.

Se identificassimo i concetti di spazio o di tempo con un solo tipo di misura sensibile e negassimo loro (per questo e giustamente) l’aggettivo “assoluto”, non ci sarebbe nessuna possibilità logica per poter asserire che altri tipi di misurazioni misurino effettivamente la stessa cosa, dal momento che si verrebbe a negare, in partenza, l’esistenza della “cosa” stessa. A meno che, come sembra fare Einstein, non affermiamo che tutti i tipi di misurazioni diano lo stesso risultato, ma questa ora diverrebbe un’affermazione empirica e come tale bisognerà verificare sperimentalmente e non può essere assunta come definizione.

Questo problema, non chiarito nella formulazione di Einstein, ha portato a diverse possibili interpretazioni della teoria della relatività, spesso non molto coerenti, specialmente quando ci si propone di salvare capre e cavoli.

Ma analizziamo, più da vicino, i concetti di spazio e tempo.

Scrive il Bridgman:¹⁸ “Abbiamo visto che le misure di lunghezza si compiono applicando metri fisici su oggetti fisici. Non possiamo misurare la distanza tra due punti dello spazio vuoto, perché se lo spazio fosse vuoto non vi sarebbe nulla con cui identificare la posizione degli estremi del metro quando lo spostiamo da una posizione a quella successiva. Vediamo dunque che dal punto di vista operativo il sistema di riferimento della geometria cartesiana, spesso immaginato in senso matematico ideale, è di fatto un sistema fisico, e che per proprietà spaziali non intendiamo altro che le proprietà di questo sistema di riferimento. Dicendo che lo spazio è euclideo, intendiamo che lo spazio fisico dei regoli misuratori è euclideo: non ha senso chiedersi se lo spazio vuoto è euclideo. La geometria, in quanto si vogliano applicare i suoi risultati al mondo fisico esterno e in quanto non la si consideri solo un sistema logico costruito sulla base di postulati, risulta pertanto una scienza sperimentale.

Abbiamo già osservato come lo spazio dell’astronomia non sia uno spazio fisico di regoli graduati, bensì uno spazio di onde luminose. Possiamo avere diverse specie di spazio a seconda delle operazioni fondamentali. Abbiamo chiamato «spazio tattile» lo spazio dei regoli graduati e «spazio ottico» lo spazio dei raggi luminosi. Chiedendoci se lo spazio astronomico è euclideo, intendiamo semplicemente chiedere se quelle caratteristiche dello spazio ottico che rientrano nel raggio delle misure astronomiche sono euclidee. L’unico atteggiamento possibile nei riguardi di tale questione e di quelle ad essa connesse, per esempio se il volume totale dello spazi o èfinito o se lo spazio è curvo, consiste nel lasciare ogni decisione all’esperimento e nel dichiarare che non abbiamo alcun diritto a nozioni preconcette. La cosa è dunque al di fuori degli scopi di questa discussione.

È interessante osservare come la teoria ristretta della relatività in sostanza presupponga, anche senza farne cenno esplicito, che lo spazio tattile e quello ottico coincidano. Questa coincidenza risulta dalle proprietà che si suppone abbiano i raggi di luce. La distanza di uno specchio si può misurare egualmente bene sia mediante un regolo, sia calcolando il tempo occorrente a un segnale luminoso per giungere allo specchio e tornare indietro. Tuttavia questa situazione è insoddisfacente, in quanto bisogna supporre che le operazioni per misurare il tempo siano definite indipendentemente, cosa che, come vedremo, non è vera. Dalla supposta equivalenza tra spazio ottico e spazio tattile consegue che il cammino di un fascio luminoso è rettilineo, la linea retta essendo determinata da operazioni compiute con i regoli. Passando ai fenomeni astronomici, le operazioni fisiche mediante regoli non si possono più effettuare e diventa privo di significato l’attribuire ai raggi luminosi su scala cosmica le stesse proprietà geometriche che attribuiamo ad essi su piccola scala.”

Stando a queste considerazioni di Bridgman, l’idea di Gauss e di Lobačevskij di verificare sperimentalmente il tipo di geometria dello spazio risulterebbe priva di senso. Al più si sarebbe solo potuto verificare se lo spazio tattile e quello ottico risultassero ancora coincidenti alle grandi distanze.

Anche la misura del tempo è soggetta a simili considerazioni. Infatti continua il Bridgman: “Dobbiamo distinguere due specie di tempo: il tempo degli eventi che hanno luogo l’uno vicino all’altro nello spazio, o tempo locale, e il tempo degli eventi che hanno luogo in punti dello spazio notevolmente lontani, o tempo esteso. Come ora sappiamo, il concetto di tempo esteso è legato inestricabilmente al concetto di spazio. Questa non è un’affermazione sulla natura, e vi si può giungere con la semplice osservazione che le operazioni mediante cui si misura il tempo esteso implicano quelle mediante cui si misura lo spazio…

Le operazioni fisiche alla base della misura del tempo non sono mai state sottoposte all’esame critico che sembra occorrere. Un metodo di misura, per esempio, implica le proprietà della luce.¹⁹ Agli estremi di un regolo graduato vengono posti due specchi ed un raggio di luce viaggia avanti e indietro fra i due specchi senza subire assorbimenti. L’intervallo di tempo occorrente per un percorso di andata e ritorno viene preso come unità, e il tempo si misura semplicemente contando tali intervalli. Questo procedimento però non risulta soddisfacente se vogliamo poter fare tutte le operazioni richieste anche dal postulato relativistico più semplice, in quanto dobbiamo essere in grado di spostare il nostro orologio da punto a punto, di trasferirlo da un sistema a un altro in moto relativo e di determinare mediante esso le proprietà dei raggi di luce nel sistema in quiete o in movimento. Riconosciamo in linea di principio che la lunghezza del metro può essere diversa quando esso è in movimento, che può cambiare anche durante l’accelerazione inerente allo spostamento del metro da un punto all’altro, e che fino a prova contraria la velocità della luce può essere funzione della velocità o dell’accelerazione. Il giuoco complicato di tutte queste possibilità ci lascia molto in dubbio sul significato fisico di postulati come, per esempio, quello secondo cui la velocità della luce è la stessa nel sistema in movimento e nel sistema in quiete. Per poter attribuire un significato semplice ai postulati sulla velocità della luce, sembra che dovremmo avere uno strumento per misurare il tempo, il quale non implichi esso stesso la proprietà della luce. Per far questo

potremmo cercare di specificare la misura del tempo in termini puramente meccanici, per esempio mediante le vibrazioni di un diapason o la rotazione di un volano. Ci troviamo però di nuovo in grandi difficoltà, in quanto dobbiamo ammettere che le dimensioni del nostro orologio meccanico possono cambiare quando esso viene posto in moto, e che anche la massa dei suoi componenti può cambiare. Vogliamo usare l’orologio come strumento fisico per determinare le leggi della meccanica, le quali naturalmente non sono determinate fino a che non possiamo misurare il tempo, e troviamo che le leggi della meccanica entrano nel funzionamento dell’orologio stesso…

I brevi intervalli di tempo acquistano quindi significato solo in connessione con le equazioni dell’elettrodinamica, che hanno una validità molto dubbia e possono venir controllate solo in termini delle coordinate spaziali e temporali che vi compaiono. Incontriamo qui lo stesso circolo vizioso di prima. Ancora una volta troviamo che ai limiti dell’esperienza attuabile i concetti si fondono l’uno con l’altro.”

Ma è proprio così disperata la situazione?

Forse le difficoltà nascono solo dal volere identificare il “concetto” di tempo con la sua “misura sensibile”. Infatti per gli antichi (da Pitagora a Newton) queste difficoltà non si ponevano. Per essi lo spazio fisico era un sistema di punti dove si potevano trasportare i punti “materiali” da un posto a un altro nello spazio dei punti “dello spazio vuoto”.

Avendo convenuto che la distanza tra due punti (materiali) assegnati era, per convenzione, l’unità di misura delle lunghezze, essa risultava indipendente dal tempo e dalla posizione; infatti sarebbe senza senso il chiedersi se la distanza tra i due punti che costituiscono gli estremi del metro campione potrebbe allungarsi per il trasporto nello spazio e nel tempo. Sarebbe come chiedersi se un’unità possa essere diversa da una unità?! Se poi si definiscono le aree e i volumi, rispettivamente, con S =L² e V = L³, lo spazio viene a risultare, per definizione, eudideo, come già detto sopra e quindi omogeneo e isotropo. Un regolo sarà “rigido”, per definizione, se il rapporto con l’unità di misura resta costante e non ha senso chiedersi se le due lunghezze possano variare entrambe allo stesso modo dal momento che non avremmo nessun modo per accorgercene.

Per quanto riguarda il tempo, per gli antichi, esso non era altro che la misura del movimento e si può dimostrare che è possibile, operativamente, individuare una misura del tempo che risulti uniforme. La clessidra degli antichi può ben essere un tale orologio; ma esaminiamo il problema con un esperimento idealizzato e, quindi, concettualmente più semplice.

Consideriamo una piccola massa (la chiameremo una pallina), in caduta libera in un tubo a vuoto di Newton, soggetta all’accelerazione costante g. Supponiamo che un orologiaio preistorico voglia costruirsi un orologio che segni un tempo uniforme (chiariremo dopo che cosa dobbiamo intendere per tempo uniforme dal punto di vista operativo, dal momento che noi non possiamo trasportare nel tempo la sua unità di misura), senza nessuna conoscenza preventiva delle leggi della fisica.

Egli comincia col costruirsi due regoli rigidi graduati, uno per misurare gli spazi percorsi dalla pallina cadendo e l’altro per misurare i tempi impiegati a percorrerli (supporremo che, al principio degli esperimenti, i regoli siano graduati allo stesso modo, stante che l’ingenuo orologiaio, non sapendo niente di fisica, suppone che un corpo in caduta libera, vicino alla superficie della terra, percorra spazi uguali in tempi uguali; del resto, questa era la convinzione di Aristotele; ma l’orologiaio ha solo fiducia negli esperimenti e non è disposto a riconoscere l’autorità di chicchessia e l’assume perciò come semplice ipotesi da verificare).

Si accorge subito che, con una sola pallina che cada lungo i due regoli, posti entrambi verticalmente e vicini tra loro, la sua ipotesi è sempre verificata. E così prende un’altra pallina identica alla prima e, facendo partire (da ferma) la prima pallina dalla cima dei regoli, fa partire la seconda (anch’essa da ferma) dalla metà dei regoli, all’istante in cui la prima pallina ha raggiunto tale quota.

Se la sua ipotesi fosse vera: le due palme dovrebbero percorrere la rimanente metà dei regoli nello stesso tempo, giungendo contemporaneamente (localmente e nello stesso sistema, aggiungiamo noi, ma l’orologiaio non è in grado di badare a tali sottigliezze, che nemmeno comprende) alla base dei regoli.

Ma si accorge subito che la sua ipotesi è sbagliata e, quindi, cancella la graduazione sul secondo regolo che, secondo lui, doveva fungere da orologio; proponendosi di segnare una nuova graduazione da trovare sperimentalmente.

Allora, per tentativi razionalmente eseguiti allo scopo di individuare la quota da cui deve lasciar cadere la seconda pallina per arrivare alla base contemporaneamente alla prima, può riuscire a incidere il primo segno sul secondo regolo (usando il metodo dei dimezzamenti successivi può raggiungere qualsiasi precisione migliore di un qualunque numero, diciamo p, preventivamente assegnato, con un numero finito di passi, esattamente n > — ln p / ln 2).

Ripetendo i suoi esperimenti, facendo partire la prima pallina da quote diverse, può tracciare la nuova scala dei tempi sul secondo regolo.

Riportando in un grafico le corrispondenti graduazioni dei due regoli otterrebbe una parabola (in questo caso ideale; nel caso generale otterrebbe, comunque, una ben determinata curva).

Se ripetendo successivamente l’intero esperimento troverà la stessa curva concluderà che il suo orologio va bene. Se (volendo usufruire di un orologio più pratico) si procurasse un fenomeno periodico che vada d’accordo con la sua graduazione, direbbe che anche il nuovo orologio segna un tempo uniforme. Se ogni volta che ripete l’esperimento, invece, trovasse curve diverse, allora direbbe che il suo orologio non va bene, perché le forze (o cause) in giuoco nel suo fenomeno non sono costanti nel tempo; ma non perderebbe, per questo, la sua fiducia nella convinzione che il “tempo assoluto” esiste, per cui proverà con altri fenomeni, magari con la luce; ed è possibile che, anche se non trovasse il fenomeno adatto, troverebbe il modo di superare l’ostacolo (p. es. mediando sulle varie curve ottenute in un lungo periodo) non essendoci alcuna compulsione logica ad abbandonare la sua idea di tempo assoluto, ché la compulsione, anzi, è in senso contrario, essendo il tempo assoluto, per lui, una necessità logica, derivante dall’esistenza del movimento, indipendente da qualsiasi metafisica che si voglia adottare.

Potrà il nostro orologiaio preistorico, che dopo i suoi esperimenti è diventato un fisico, passare dal suo tempo locale (o, comunque, quasi locale) al tempo esteso? Se privo di pregiudizi metafisici potrebbe fare la stessa osservazione di Einstein, naturalmente se fosse portato a credere che la velocità della luce fosse costante nel suo sistema quando misurata facendo uso di corpi rigidi e di orologi meccanici.

Sul significato effettivo delle trasformazioni di Lorentz e della teoria della relatività, cioè se le conseguenze dipendano solo da una nuova convenzione per misurare lunghezze e tempi, o se, al contrario, esse comportino una reale modificazione fisica degli orologi e dei regoli rigidi per effetto del loro movimento, i pareri sono sempre stati discordi anche per coloro che dichiarano di accettare in toto la teoria.

Senza schierarci, momentaneamente, per l’una o per l’altra tesi, esaminiamo alcune conseguenze della teoria sul piano puramente metrologico.

La relazione che lega tra loro le lunghezze di un’asta rigida, come misurate dai due classici osservatori della teoria della relatività ristretta, è data da L’ = γ L.

Poiché γ è una grandezza adimensionata la relazione può essere scritta

(avendo indicato con l ed i valori numerici e con e le rispettive unità di misura).

Noi siamo sempre liberi di includere (vedi Perucca) il coefficiente γ o tra i valori (con ) o tra le unità di misura (con) o, anche, possiamo fare altre convenzioni più convenienti a seconda dei casi e delle nostre necessità.

Nel primo caso noi siamo obbligati a misurare le due grandezze, riferentesi alla stessa asta, con la stessa unità di misura. Non sapendo se effettivamente i regoli si allunghino per effetto del movimento, se vogliamo essere sicuri che l’unità di lunghezza sia la stessa, dobbiamo effettuare le misure nello stesso riferimento e quindi con metodi diversi, l’una per confronto diretto, l’altra, necessariamente, impiegando segnali luminosi. Non potremo mai decidere, in questo caso, se il fatto che y sia diverso da 1 sia solo apparenza o una modifica effettiva delle lunghezze.

Nel secondo caso, si deve supporre, fin dal principio, che l’allungamento dell’asta in movimento sia effettivo, essendo le unità di misura vere “grandezze” e non semplici numeri; ma, in tal caso, i valori misurati dai due osservatori (cioè i “numeri” trovati) risulterebbero sempre identici nei due sistemi e, quindi, entrambi gli osservatori sono legittimati a usare la meccanica classica e a non menzionare più il fatto che hanno bisogno di segnali luminosi per comunicare, perchè il fatto risulterà assolutamente irrilevante per tutti i loro esperimenti, che ognuno di essi è “obbligato” a compiere nel suo proprio sistema, non potendo uscirne fuori, in quanto misure per confronto diretto, sia di distanze che di tempi, si possono fare “solo” nel “proprio” sistema di riferimento.

Si potrebbe, ancora, pensare che sia: .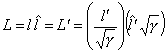

Lo stesso discorso vale per qualunque altra grandezza.

È utile approfondire la questione a partire dalle ipotesi con cui vengono derivate le trasformazioni di Lorentz.

Einstein, nel suo primo lavoro sulla relatività²⁰, comincia con l’osservare che la teoria che vuole sviluppare “si appoggia, — come ogni altra elettrodinamica — sulla cinematica del corpo rigido, poiché le dichiarazioni di una di quelle teorie riguardano i rapporti fra corpi rigidi (sistemi di coordinate), orologi e processi elettromagnetici. Le non sufficienti considerazioni di questa circostanza è la radice delle difficoltà con le quali l’elettrodinamica dei corpi in moto ha presentemente da lottare.”

Quindi, continua: “Sia dato un sistema di coordinate nel quale valgano (si intende: in prima approssimazione) le equazioni meccaniche newtoniane. Noi denominiamo questo sistema ... «sistema in quiete». Se un punto materiale è fisso relativamente a questo sistema di coordinate, la sua posizione relativa a quest’ultimo può venir determinata per mezzo di aste di misura rigide, impiegando i metodi della geometria euclidea espressa in coordinate cartesiane.” (le sottolineature sono nostre).

Avendo notato che, nel caso di sistemi in moto rispetto a un ipotetico riferimento in cui si suppone che si propaghi la luce, si devono riscontrare differenze tra le misure di distanza tra due punti, effettuate per confronto diretto con l’asta rigida di misura, rispetto a quelle effettuate misurando il tempo impiegato dalla luce a percorrere la stessa distanza e ciò a causa della difficoltà che si hanno non conoscendo il riferimento in quiete assoluta (ammesso che esista), procede ad estendere la nozione di contemporaneità a grandi distanze. Decide di “definire” la contemporaneità mediante l’istante di tempo che si può trovare divendo per due il tempo impiegato dalla luce per andare e venire da un posto assegnato in cui si suppone posto un orologio che si voglia sincronizzare.

Decide, ancora, che si può fare a meno di un riferimento in quiete assoluta ed enuncia due postulati:

“1. Le leggi, secondo le quali si modificano gli stati dei sistemi fisici, sono indipendenti dal fatto che questi cambiamenti di stato vengano riferiti all’uno o all’altro di due sistemi di coordinate che si trovano in relativa reciproca traslazione uniforme.

2. Ogni raggio di luce si muove nel sistema di coordinate «in quiete» con la determinata velocità V, indipendentemente dal fatto che quel raggio di luce sia emesso da un corpo in quiete, o da un corpo in movimento. Con ciò è

Percorso della luce

Velocità = ^{_________________________}

Durata del tempo

ove «durata del tempo» è da intendere nel senso della definizione precedentemente data”.

E conclude: “Vediamo dunque che al concetto di contemporaneità non possiamo attribuire alcun significato assoluto, ma che invece due avvenimenti che, considerati da un sistema di coordinate, sono contemporanei, considerati da un sistema mosso relativamente ad esso, non sono più da considerare come avvenimenti contemporanei.

Ciò è assolutamente vero solo se si specifica ulteriormente; e precisamente ricordando: “se conveniamo di misurare tempi e distanze nel modo convenuto”.

In altre parole: la relatività si ha rispetto ai “mezzi di osservazione” e non rispetto al “sistema di riferimento”, per usare (anche se con diversa bipartizione) il vocabolario di Fock, che era inteso a distinguere tra la relatività della meccanica quantistica da quella della teoria di Einstein.

Questo slittamento semantico (tra i due detti modi di intendere l’aggettivo “relativo”) si avverte in tutto l’articolo di Einstein e lo porta a una derivazione delle trasformazioni di Lorentz inutilmente complicata e anche sbagliata in quanto, implicitamente, si fa un’ulteriore e non giustificata ipotesi oltre alle due esplicitamente enunciate come 1. e 2. di cui sopra; e cioè quella di scambiare una precisa “ipotesi fisica”, tutta da verificare, per una “definizione” di contemporaneità, per cui ritiene naturale assumere che due osservatori, in moto relativo, che usino la luce come mezzo di comunicazione, debbano osservare gli stessi effetti sia che reciprocamente si avvicinino, sia che reciprocamente si allontanino, cosa che, invece risulta empiricamente assolutamente falsa, indipendentemente da qualunque possibile trasformazione di coordinate.

Sulla possibile diversità della nozione di contemporaneità, in relazione ai diversi metodi empirici di misura, in effetti, sembra che Einstein abbia presente, in qualche modo, il problema; ma non ci insiste più di tanto. Infatti, nel considerare il ritardo reciproco tra due orologi (sincronizzati secondo le sue regole), uno dei quali, dopo avere percorso una linea chiusa a velocità costante (in modulo), si ritrovi nuovamente a coincidere con l’altro (questo problema, in seguito all’interpretazione di Langevin, è diventato il paradosso dei gemelli), Einstein precisa: “Si conclude da ciò che un’orologio che non ha necessità di rimanere fisso [notiamo qui che secondo Einstein, sembrerebbe che, quantomeno, si debbano escludere gli orologi che, come gli orologi a pendolo, dipendano da una proprietà locale, come la gravità, per funzionare] il quale si trovi all’equatore, deve procedere più lentamente di un piccolo importo che un orologio esattamente eguale e sottoposto a eguali condizioni, che si trovi al polo”.

Queste parole ci fanno capire che per Einstein la misura dei tempi è relativa ai tipi di orologi che usiamo. Quindi, per poter parlare di tempo in astratto, l’alternativa è: o ci riferiamo al tempo “assoluto” di Newton definito logicamente e indipendentemente dal modo di come concretamente lo misuriamo; o specifichiamo esattamente le operazioni concrete con il quale lo misuriamo ed esso ora sarà “relativo” ai mezzi di osservazione, cioè se cambiamo il modo di misurarlo dobbiamo trovare la precisa relazione fisica che lo lega al precedente. Ma questo, ovviamente, vale per qualunque grandezza fisica e, in particolare, anche per lo spazio, in quanto considerato come luogo delle posizioni relative dei suoi punti, definite per mezzo di misure di lunghezza. E ciò non basta: bisognerà, se optiamo per la seconda possibile scelta, distinguere tra un “tempo locale” e un “tempo esteso”.

Notiamo, tuttavia, che nei successivi lavori Einstein semplifica la dimostrazione sulla base della formulazione di Minkovski e, anche se in modo non esplicito, tenta una giustificazione dell’ipotesi nascosta, non accorgendosi che dietro il nuovo formalismo quadridimensionale si nasconde una precisa ipotesi di ordine metafisico (che d’altronde era ben chiara al Minkovski,²¹ in un primo tempo Einstein non aveva capito la necessità della nuova veste matematica che alla sua teoria aveva dato il suo ex professore e la considerava come “un inutile sfoggio di erudizione matematica”) che sembra in contraddizione con la teoria delle grandezze; fatto questo che emerge chiaramente quando si utilizzi il calcolo sulle grandezze come descritto nei passi soprariportati di Peano e nella Fisica del Perucca già menzionata.

Vediamo di ricostruire la dimostrazione di Einstein (ma tenendo conto della teoria delle grandezze, di cui alle citazioni di Peano e di Bridgmann e come dettagliatamente sviluppata dal Perucca e come usata da ogni fisico sperimentale).

Svilupperemo una particolare interpretazione della teoria della relatività (ristretta) proposta da Synge e da questi esposta con la usuale confusione tra grandezze e numeri,²² confusione che, se potrebbe essere tollerata in fisica classica, è assolutamente pericolosa nella fisica relativistica, quando si voglia stabilire il significato fisico delle trasformazioni di Lorentz, fatto che è confermato dalle infinite proposte interpretative avanzate nel passato e che si continuano ad avanzare perennemente.

***

Saremo ora costretti ad usare un linguaggio piuttosto tecnico; quindi, il lettore a cui non siano familiari i simboli matematici può, se vuole, saltare ai successivi tre asterischi.

Converremo di usare le lettere maiuscole per indicare le grandezze, le corrispettive lettere minuscole per indicare le relative misure e le lettere minuscole con un apice ^ per indicare le rispettive unità di misura.

Useremo le lettere segnate con ′ per le quantità che si riferiscono al sistema in moto, per distinguerle dalle corrispondenti quantità nel sistema in quiete.

Supponiamo che i due osservatori O e O′, di cui parla Einstein nel lavoro sopracitato, scelgano la stessa origine delle coordinate al tempo t′ = t = 0 e decidano entrambi di usare la luce per misurare le distanze ognuno nel proprio sistema.

Per quanto si può leggere nell’articolo di Einstein, possiamo dedurre che ognuno dei due osservatori può immaginare di avere a che fare con spazi e tempi assoluti, nel preciso senso che gli attribuiva Newton, e non in quello che spesso viene attribuito a Newton (d’altronde, ipotesi necessaria se si pretende che i due osservatori possano fare misure per confronto diretto, ognuno all’interno del proprio sistema; questa assunzione verrà, nei successivi lavori, abbandonata da Einstein perché, come vedremo subito, è incompatibile con le trasformazioni di Lorentz, quando non si vogliano fare ipotesi inaccettabili e se si vuole mantenere alla teoria il suo ruolo di “teoria fisica” e non quello, puramente estetico, di riscrittura delle equazioni della meccanica).

Per l’ipotesi della relatività, come formulata nella 1., basterà considerare solo quello che può dedurre il primo osservatore, in quanto il secondo ragionerà esattamente allo stesso modo.

Come già abbiamo avvisato, useremo l’aggettivo “assoluto” nel senso newtoniano e cioè quello definito da regoli rigidi, che si possono trasportare; e di tempo uniforme e indipendente dallo spazio. Non supporremo, però, l’esistenza di uno spazio assoluto in “quiete assoluta”.

Sia P la posizione (“assoluta”) al tempo T (“assoluto”) di una particella materiale secondo il primo osservatore. Sia O l’origine delle sue coordinate ed O′ la posizione dell’origine delle coordinate del secondo osservatore, come vista dal primo osservatore.

Per il primo osservatore, dal momento che il suo spazio è euclideo e che tempi e distanze sono misurate con operazioni indipendenti, si ha:

Se poniamo:

possiamo scrivere:

(1) .

Siano ora R e T le coordinate (spaziali e temporali) di un evento dato per O.

Supponiamo che, all’istante opportuno T_p, O lanci un segnale luminoso verso R. Sarà ricevuto al tempo (avendo posto R = | R | e C = | C | ). Sarà di ritorno al tempo .

Calcolerà:

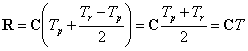
Secondo le vedute di O, perché O′ possa ricevere, propriamente, il segnale di ritorno, O′ dovrà lanciare il segnale al tempo T₁, istante in cui si troverà in una certa posizione R₁ (come misurata da O), tale che il segnale possa giungere in R al tempo

(2)

ed essere ricevuto, di ritorno da O′, al tempo

(3) ,

essendo R₂ la posizione di O′ al tempo T₂.

Ricordiamo che R₁, R₂, T₁, T₂ si intendono tutte misurate nel riferimento di O. Per trovare più semplicemente le relazioni opportune tra le varie grandezze poniamo:

(4) .

Naturalmente si ha:

(5) .

Da (2), (3), (4) si ha:

(6)

(notiamo che per O l’intervallo di tempo impiegato dal segnale per andare da O′ a R è diverso dal tempo impiegato per ritornare in O′, il primo intervallo sarà maggiore o minore del secondo a seconda che O e O′ si allontanino o si avvicinino reciprocamente).

Avendo posto:

(7) ,

per somma e sottrazione delle due equazioni in (6), si ottiene:

(8)

(9) .

Dalle definizioni di D ed S si trova:

(10)

e ancora, tenuto conto delle definizioni precedenti:

(11) .

da cui

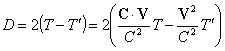
e, quindi, anche:

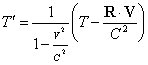
Se usiamo le stesse unità di misura per misurare V e C, si avrà: e quindi:

(12) .

Per il principio di relatività, O immagina che il secondo osservatore scriverà

(13) ,

che per la (12) può scriversi:

(14) ,

ricordando che per (1), (5), (13) si ha

.

e quindi

,

la (14) si può scrivere:

(15) .

Le formule precedenti, per il modo in cui sono state ricavate, obbediscono ai due postulati di Einstein e alla sua definizione di contemporaneità.

Vediamo se i due osservatori possono scegliere unità di misura tali da ottenere le trasformazioni di Lorentz.

Sostituendo alle grandezze le loro espressioni in termini di valori e di unità di misura e ponendo (come è necessario per non violare il principio di relatività):

e ; e ponendo, ancora, , vediamo quali ipotesi ulteriori dobbiamo fare per scrivere le trasformazioni di Lorentz relative alle quantità numeriche.

Le (15),(12) diventano:

(16) ,

(17) ,

se poniamo, per convenzione, e , (notiamo che con tale scelta i valori numerici della velocità relativa e della velocità della luce non possono coincidere per i due osservatori, — cioè e — a meno che non si abbia γ = 1) otteniamo

;

e, infine, avremo:

(18) ,

(19) .

Queste non sono esattamente le trasformazioni di Lorentz, infatti, quando si sceglie per entrambi i sistemi, l’asse x come direzione della velocità relativa si ottiene:

,

invece di

.

Ma le formule usuali (più corrette?!) si possono facilmente ottenere cambiando leggermente le convenzioni, decidendo di scegliere, nella direzione del moto, unità di misura diverse da quelle di tutte le altre direzioni, arrivando alle formule usuali:²³

(20)

(21) .

***

In linea di principio, “non abbiamo alcun modo di verificare le convenzioni che abbiamo fatto sulle unità di misura”, perché riguardano un “impossibile” confronto diretto tra due sistemi in movimento relativo. In teoria, potremmo verificare la coincidenza, anche per osservatori in moto qualsiasi, tra spazio tattile e spazio ottico (ma questo è un altro problema che non ha niente a che vedere con il primo che, come abbiamo detto, non è verificabile per sua natura). Si ritiene che l’esperimento di Michelson e Morley abbia deciso questa questione. Ma molti in passato hanno contestato il risultato dell’esperimento, alcuni contestandone l’accuratezza dal punto di vista sperimentale, altri contestandone la teoria usata per predire il risultato dell’esperimento, nel senso che alcuni (in particolare il Righi²⁴) hanno mostrato che usando correttamente il principio di Huygens si deve ottenere (classicamente) il risultato che effettivamente è stato trovato sperimentalmente. Altri ancora negando che l’esperimento possa avere qualcosa a che fare con il problema in discussione.

L’impressione che si ricava, leggendo la letteratura odierna sull’argomento, è che l’accordo tra teoria ed esperimento sembra essere diventato solo una questione di fede, come la materia del catechismo con il quale ho cominciato il mio discorso.

Ma, in ogni caso, l’esperimento di cui sopra, quando lo si voglia interpretare come una prova della coincidenza dei due spazi (ma su questo si possono avanzare serissimi dubbi), non cambierebbe niente sulle convenzioni riguardo alle unità di misura, che bisognerà sempre fare; al massimo, potrebbe solo dire che non esistono osservatori privilegiati.

Ecco perché, in seguito, Einstein (dopo la formulazione puramente “geometrica” di Minkovski) abbandona ogni riferimento alle diverse operazioni di misura nei due sistemi di riferimento e si limita a postulare l’invarianza del quadrintervallo, del quale non v’è alcun cenno nel primo articolo.²⁵

Successivamente è costretto ad asserire:²⁶ “Né il punto dello spazio, né l’istante del tempo in cui qualcosa accade, hanno una realtà fisica, ma soltanto l’evento in se stesso. Non vi è alcuna relazione spaziale assoluta, cioè indipendente dallo spazio di riferimento, né alcuna relazione temporale assoluta tra due eventi, ma vi è soltanto una relazione assoluta nello spazio e nel tempo, cioè indipendente dallo spazio di riferimento, come apparirà nel seguito.”

Sul perché Einstein volesse ritrovare ad ogni costo le trasformazioni di Lorentz non c’è dubbio alcuno, perché lo stesso Einstein dichiara che il suo scopo principale era quello di trovare le stesse trasformazioni sia per i fenomeni elettromagnetici che per quelli meccanici, dando la preferenza ai primi, essendo per lui inconcepibile, anche a livello emotivo, l’idea dell’azione a distanza. Infatti, già molto tempo prima del Lorentz, era stato dimostrato dal Voigt²⁷ che quelle trasformazioni (ora chiamate di Lorentz) rendevano invariante l’equazione del moto di una perturbazione locale, in un mezzo non dispersivo, propagantesi con velocità costante, trasformazioni valide anche per i fenomeni meccanici (a parte il valore della velocità di propagazione) e non solo per l’elettromagnetismo (ammesso che si possa trovare un modello fisico, quindi sperimentalmente verificabile, a partire da misure di grandezze fisiche e non a partire da non misurabili — senza l’intermediario delle prime — quantità numeriche); quindi, alla fin dei conti, Einstein voleva eliminare le particelle dal linguaggio della fisica; e dobbiamo dire che c’è riuscito, a costo di ulteriori complicazioni che, probabilmente, ci costringono ad abbandonare completamente la teoria delle grandezze, con buona pace dei fisici sperimentali e degli antichi scienziati.

Ma, comunque, ci restano i numeri di Dedekind e di Cantor e la geometria di Hilbert e possiamo continuare a vivere beati con la consolante filosofia platonico-aristotelica, tanto deprecata da Bacone, ingiustamente, perché non apprezzava i discorsi consolatori!

L’esportazione di tale particolare metafisica della matematica ai problemi della gravitazione universale ci ha condotto al di là di ogni ragionevole immaginazione.

Gli antichi Cinesi cui accennava Peano nella citazione che abbiamo sopra riportato, hanno scoperto il raggio del mondo mediante l’osservazione.

Ma noi moderni siamo riusciti a scoprire, addirittura, il raggio dello “spazio”, senza bisogno di osservare alcunché, con la sola potenza del pensiero.

Per poter parlare di fisica finora ci sono bastati i numeri di Dedekind; ma, per poter parlare cli economia politica, occorrerà ricorrere ai numeri transfiniti di Cantor.

Un bel giorno, un mio amico economista mi ha chiesto se, per caso, ero in grado di spiegargli quella strana matematica che si impiega nella teoria dei “beni pubblici”.

Mi ha detto che il valore di un bene pubblico era una quantità proporzionale ai benefici, che pare che siano una misura della soddisfazione che ogni cittadino prova nell’usufruire del bene pubblico; mi portava l’esempio, allora, della base missilistica di Comiso, figurarsi la mia soddisfazione! La cosa strana, e che d’altronde bisognava capire, era come mai questa quantità, la stessa per tutti i cittadini, poteva mai risultare uguale alla loro somma.

Gli ho detto che, forse, il beneficio del cittadino veniva calcolato dividendo il costo dell’opera per il numero degli abitanti. Mi ha detto che ciò era impossibile; ché egli, se fosse stato così, l’avrebbe facilmente capito.

A riprova mi ha mostrato diversi libri ed articoli di riviste dove si poteva leggere:²⁸

.

Gli ho detto che quelle strane quantità potevano solo essere i numeri transfiniti di Cantor o i numeri non standard di Robinson, e quindi per me non erano quantità, ma semplici sciocchezze.

Il mio amico se ne è andato, sicuramente pensando, e sicuramente a ragione, anche se non me l’ha detto, che io non capivo un bel niente nè di economia, nè di matematica; perché era assolutamente impossibile che a qualcuno avessero potuto dare il premio Nobel per l’economia (mi ha detto che glielo avevano davvero dato; a dire il vero, io non mi sono sorpreso del fatto) per avere inventato delle semplici sciocchezze.

Molti ripetono che la scienza moderna si occupa solo di “fatti” e che le teorie sono vere solo se spiegano i fatti.

Non è chiaro il significato di “fatto” e nemmeno quello di “spiegazione”; gli epistemologi le hanno inventate tutte!

È noto che teorie assolutamente false e contraddittorie possono spiegare i fatti, anzi “tutti” i fatti (specialmente se i fatti si inventano di sana pianta, in effetti sembra difficile oggi distinguere tra fatti e modelli; c’è chi ci ha scritto sopra libri interi). E qualcuno, invece, pensa, ed io tra questi, che quello che conta non sono i fatti ma la loro interpretazione (basta pensare ai “fatti” che oggi succedono nel Golfo Persico).

Si dice che Keplero abbia scoperto le sue famose leggi perché, in base alla sua filosofia mistico-religiosa, era convinto che i pianeti, nel loro volgere, suonassero una bellissima armonia secondo le migliori regole del contrappunto.

Newton si è valso di tali leggi per una filosofia tutta diversa.

Ma è divertente, in proposito, un aneddoto personale che, allora, mi fece venire molti pensieri sul ruolo delle teorie; a me, che ero completamente digiuno di epistemologia.

Ero fresco della mia laurea in fisica e un mio amico mi ha voluto presentare un suo conoscente che voleva investire del denaro per sfruttare l’invenzione di un contadino che si vantava di avere inventato un dispositivo che, automaticamente, suonava l’allarme in caso di fughe di gas in un luogo chiuso.

Il giovane imprenditore pretendeva che, date le competenze che egli pensava che io dovevo possedere, bisognava che lo accompagnassi per verificare se il contadino non avesse avuto, per caso, l’intenzione di imbrogliarlo; diceva, oggi non ci si può più fidare di nessuno!

Spinto anche dalla curiosità sono andato in una casa di campagna nei dintorni di un paesino etneo, insieme all’imprenditore ed al nostro amico comune.

Il dispositivo, che il contadino ci ha mostrato, funzionava veramente. Aprendo una bombola di gas faceva suonare un campanello del tipo di quelli che si usano negli ingressi di casa.

Ho cercato di capire come funzionasse il marchingegno e ho pregato il contadino di aprire la scatola che lo conteneva. Era di una semplicità estrema! Dentro la scatola metallica a forma di parallelepido, fatta con delle latte di conserva, c’era, sistemato nel mezzo, un mattoncino di un impasto terroso, che aveva l’apparenza di essere stato indurito al sole e che divedeva la scatola in due parti uguali. Una parte comunicava con la bombola di gas, mediante un tubicino di gomma. Dall’altra parte della scatola era sistemato un relè che, per effetto della pressione del gas sulla parete di latta della scatola, chiudeva un circuito elettrico che azionava la suonerìa. E questo era tutto!

Nonostante la strana teoria fisica del contadino, mi è parso di capire che l’oggetto essenziale doveva essere quello strano mattoncino terroso.

Infatti sapevo (l’avevo letto nel libro di Fisica del Perucca) che ci sono dei materiali che sono, nei processi di diffusione, selettivi per i diversi gas, a seconda del loro peso molecolare.

Per cui ho pensato che il mattoncino poteva ben essere impermeabile all’aria ma permeabile al butano della bombola. Questo faceva aumentare la pressione nello scomparto dove stava il relè, che chiudeva il circuito, così azionando la suoneria.

Ma qualunque fosse la corretta teoria fisica per la spiegazione del fenomeno, la cosa più strabiliante per me fu la teoria con la quale, invece, il contadino era riuscito nell’impresa, dopo dieci anni (così egli diceva) di innumerevoli tentativi falliti.

Secondo il suo racconto, il tutto cominciò in seguito alla morte del fratello a causa di una fuga di gas. Egli decise che bisognava inventare qualcosa per impedire tali accidenti. Da dove partire? La sua teoria era molto semplice: nel mondo ci sono due forze contrastanti, da una parte il bene, rappresentato dall’angelo e, dall’altra il male, rappresentato dal diavolo. Fin qui capivo, mi ricordavo della maestra di catechismo.

Senza alcun dubbio il fratello era morto a causa del diavolo che aveva approfittato del fatto che nei luoghi chiusi e specialmente in presenza del gas, che era “il male”, l’angelo, che rappresentava “il bene”, non poteva certamente stare.

Quindi, per prima cosa, bisognava creare una situazione in cui l’angelo potesse essere presente anche se separato dal diavolo.

Ecco l’idea della scatola divisa in due comparti nettamente separati, il tubo del gas, ovviamente, dalla parte del diavolo e il campanello d’allarme, altrettanto ovviamente, dalla parte dell’angelo.

Ma la prova non funzionò, forse perché: se i due stanno nettamente separati non possono azzuffarsi. E la lotta tra il bene e il male è essenziale per la buona riuscita dì ogni cosa (mi viene ancora da pensare alla guerra del Golfo).

Bisognava trovare il setto divisorio adatto. Dieci anni ci son voluti per trovarlo, ma ci è voluto anche l’intervento della provvidenza divina.

Un giorno si trovava alle foci dell’Alcantara. Aveva camminato a piedi nudi e sentiva il bisogno di lavarseli li, sull’argine. Era una bella giornata. Notò il colore del fango in riva al fiume; era bellissimo, bianchiccio; non aveva mai visto un fango di un colore così bello e delicato. Un fruscio di arbusti là vicino lo avvertì che finalmente aveva trovato quello che cercava. Il fruscio degli arbusti era la voce del Signore.

Svuotò la gavetta del suo mangiare e la riempì di quella poltiglia miracolosa. Lungo la strada del ritorno andò ruminando sul come fare indurire quella poltiglia. Una forma adatta e il sole sarebbero bastati.

Dopo qualche prova il marchingegno funzionò e ora egli era pronto a far fruttare la sua invenzione che aveva avuto anche la benedizione di Dio.

Ho concluso che tutte le teorie sono buone a spiegare i fatti sperimentali, anzi a produrre invenzioni in qualche modo commerciabili.

Da allora ho preteso che le teorie scientifiche, per essere tali, non dovevano limitarsi a spiegare i fatti o a produrre invenzioni.

La coerenza sintattica non mi bastava più. Pretendevo la coerenza semantica; e ... non solo!

Avrei pure preteso la coerenza totale con la mia visione del mondo; ma, sfortunamente, quest’ultima non la si può pretendere dagli altri e la scienza dovrebbe, invece, essere oggettiva, nel senso che non dovrebbe essere influenzata da quest’ultimo fattore. Non so come risolvere questa contraddizione, chissà se mi potrebbero aiutare i numeri transfiniti.

Ho capito, in seguito, che tutti vogliono escludere quest’ultimo fattore dalla scienza. Ma il guaio è che identificano l’oggettività proprio con la propria personale visione del mondo o con quella degli uomini più influenti.

Non so più se può esistere una scienza che possa fare a meno della fede, come prima ingenuamente pensavo.

Il mio diavolo mi ha messo nei guai e non sono riuscito a trovare l’angelo, come invece è capitato al fortunato contadino inventore.

Catania, 20/2/1991.

NOTE

1. A. Eddington, Space, time and gravitation, Harper, 1959. TORNA
2. A. Einstein, L. Infeld, L’evoluzione della fisica, Einaudi, 1953, p. 233 e segg. TORNA
3. Per alcune importanti critiche registratesi nel passato cfr. A. Pagano, Su di un’opera dimenticata di fisica di Boggio e Burali-Forti, Mondotre/Quaderni, Ott. 1989, Siracusa; e anche il suo articolo in questo stesso numero dei Quaderni. TORNA
4. G.Peano, Opere Scelte, vol. II, Ed. Cremonese, Roma, 1958, p. 117. TORNA
5. G.Peano, Opere Scelte, vol. III, op. cit., p. 268; M. Pieri, Opere sui Fondamenti della Matematica, Ed. Cremonese, 1980, p. 455. TORNA
6. Scriveva Bacone nel Novum Organum: “Oggi la filosofia naturale non si trova nella sua forma pura ma è infettata e corrotta: nella scuola di Aristotele per mezzo della logica, nella seconda scuola di Platone, di Proclo e consoci per mezzo della matematica, tali strumenti devono portare a compimento la filosofia naturale e non generarla o procrearla”. TORNA
7. Osserviamo che se si divide un triangolo rettangolo isoscele con un segmentoche divide in due l’angolo retto si vengono a formare due altri triangoli rettangoli isosceli uguali tra loro e, quindi, ciascuno di area metà del primo. Questo fatto, insieme alla definizione di area di un triangolo, implica che la somma degli angoli di un tale triangolo è uguale a due retti. Ma, come già il Saccheri ha dimostrato (cfr. R. Bonola, La Geometria Non-Euclidea, Zanichelli, 1906, p. 25-26), se tale proprietà vale in un caso varrà in tutti i casi e risulterà valido il postulato delle parallele. La maggior parte dei commentatori moderni nega la validità delle dimostrazioni del Saccheri e del Wallis, e di molti altri antichi commentatori dell’opera di Euclide. L’argomento col quale si nega la validità di tali dimostrazioni è oltremodo divertente: invece di partire dagli assiomi di Euclide, come facevano gli antichi commentatori, si parte, invece, dagli assiomi di Hilbert! È banale osservare che qualunque dimostrazione può risultare valida o non valida se si cambiano gli assiomi. TORNA
8. Opere Scelte, vol. III, op. cit., p. 141. TORNA
9. Cfr. N. I. Lobačevskij, Nuovi principi della geometria, Boringhieri, 1974, p. 39. TORNA
10. Ibidem, p. 61-63. TORNA
11. Oggi si chiama: geometria non-euclidea iperbolica. TORNA
12. Cfr. Hertz, Miscellanous Papers, Vol. III, Principles of Mechanics, Macmillan, 1896. TORNA

13. “Caeterum harum potestatum, nempe motus, vis, ... , quantitas duplici ratione aestimatur; utpote vel secundum intensionem earum vel extensionem” = “Inoltre queste quantità, cioé moto, forza, ... , si possono considerare in modo duplice, cioé sia secondo l’intensione, sia secondo l’estensione”. Cfr. Newton, De gravitatione et equipondio fluidorum, Unpublished scientific papers of Isaac Newton, Cambridge Univ. Press, 1962. TORNA

14. Operazioni sulle grandezze, in Opere Scelte, vol. III, op. cit., p. 435 e segg. TORNA

15. Altro nome usato da Lobačevskij per la sua geometria. TORNA

16. Per ulteriori dettagli in questioni di metrologia cfr. E. Perucca, Fisica Generale e Sperimentale, I, UTET, 1949, p. 5-90. TORNA

17. P. W. Bridgman, La logica della fisica moderna, Einaudi, 1952, p. 98-99; Bridgman ha ricevuto il premio Nobel per le importanti sue ricerche sperimentali nel campo delle fisica dei materiali alle altissime pressioni ed è stato sempre attento ai problemi epistemologici; nel libro di cui sopra, nella prefazione, leggiamo: “Questa escursione nel dominio della critica dei fondamenti, da parte di uno scienziato le cui attività si sono finore limitate quasi totalmente al campo delle esperienze, non dipende da un decadimento senile, come qualche spregiudicato potrebbe supporre. Ho sempre sentito, nel corso dei miei lavori sperimentali, l’esigenza impellente di una migliore comprensione dei fondamenti del nostro pensiero fisico, e per molto tempo ho tentato in modo più o meno sistematico di raggiungere questa comprensione. ... Nonostante i precedenti scritti sui fondamenti della scienza in genere, di Clifford, Stallo, Mach e Poincaré, per non citare altri, credo che un nuovo saggio critico non abbia bisogno di giustificazione”; perché, come dice nell’introduzione: “Una delle novità più notevoli della fisica recente è il cambiamento di atteggiamento verso quello che si può chiamare l’aspetto interpretativo della fisica. Si va riconoscendo sempre più, sia negli scritti che nelle conversazioni dei fisici, che il mondo degli esperimenti non è comprensibile senza un esame dello scopo della fisica e della natura dei suoi concetti fondamentali. ... Il fisico medio tende ad evitare di interessarsi a tali questioni ed a liquidare le speculazioni dei colleghi definendole “metafisiche”. …Tuttavia la crescente reazione in favore di una maggiore intelligenza dei fondamenti interpretativi della fisica ... rappresenta ... una nuova tendenza cominciata senza dubbio con la teoria einsteiniana della relatività ristretta.” TORNA

18. Op. cit., p. 73-84. TORNA

19. A proposito di questo argomento toccato qui dal Bridgman, scriveva Einstein nel 1922 (cfr. A. Einstein, Il significato della relatività, Einaudi, 1955, p. 37): “Si critica spesso la teoria della relatività perché attribuisce senza giustificazione un’importanza concettualmente preminente alla propagazione della luce, in quanto fonda il concetto del tempo sulla legge della propagazione della luce. La cosa sta tuttavia pressappoco in questi termini. Per attribuire un significato fisico al concetto di tempo si richiedono processi che permettano di stabilire delle relazioni fra posti differenti. Non ha importanza quali tipi di processi si scelgano per una tale definizione del tempo, ma è teoricamente vantaggioso scegliere soltanto quei processi sui quali si conosca qualcosa di sicuro. Ciò vale per la propagazione della luce nel vuoto in una misura maggiore che per qualunque altro processo che si possa considerare, grazie alle indagini di Maxwell e di H. A. Lorentz.” Ma su quest’ultimo punto, in seguito, Einstein ha cambiato opinione, infatti: “Le 12 décembre 1951, presquè à la fin de sa vie, il écrivait ce qui suit á son vieil ami Michele Besso, avec qui, jadis, au Bureau des brevets, il avait discuteé ses idées naissantes: «Cinquante ans à ruminer sans trêve, et me voici sans plus de réponse qu’au premier jour á la question de savoir ce que sont les quanta de lumiére. De nos jours, Pierre, Paul ou Jacques s’imagine qu’il a une réponse, mais il se trompe.»”, tratto da: Banesh Hoffman, Albert Einstein, créateur et rebelle, Édition du Seuil, 1975, p. 203. TORNA

20. A. Einstein, Zur Elektrodynamik bewegter Körper, Annalen der Physik, 17, 1905, p. 891; vedi la traduzione in italiano di P. Straneo riportata in: Cinquant’anni di relatività, (a cura di Pantaleo), Universitaria Editrice, Firenze, 1955. TORNA

21. In una sua lezione, tenuta nel 1908, Minkowski comincia: “Le concezioni su spazio e tempo, che vorrei sviluppare per voi, sono cresciute sul terreno fisico-sperimentale. … D’ora in avanti lo spazio in sé e il tempo in sé sono destinati a sprofondare completamente nell’ombra e solo una specie di loro commistione potrà mantenere un’esistenza autonoma.” TORNA

22. J. L. Synge, Relativity: The special theory, North Holl. Pu. Co., 1956. TORNA

23. Le equazioni vettoriali (20) e (21) si possono trovare in A. Katz, Classical Mechanics, Quantum Mechanics, Field Theory, Academic Press, 1965, p. 167. TORNA

24. A. Righi, Nuovo Cimento, XVI, p. 213, 1919. Potrebbe sembrare strano che nessuno mai abbia fatto riferimento a questo lavoro né per contestano né per approvarlo, ma secondo la teoria di Kuhn questa sarebbe giusto la norma. TORNA

25. Tale ipotesi equivale all’assunzione di Einstein, che a un certo punto è costretto a fare per ritrovare le trasformazioni di Lorentz, di equivalenza tra osservatori in moto di avvicinamento o in allontanamento reciproco. Nella formulazione in coordinate di Einstein (e di tutti i posteriori autori) questo potrebbe sembrare un semplice cambiamento di coordinate; ma, in effetti, come risulta ovvio in un linguaggio “assoluto” (cioè senza l’inutile intermediazione delle coordinate), è un fatto fisico indipendente dalla scelta del sistema di coordinate. Spesso tra i “giustificazionisti” viene confuso con le proprietà di invarianza per trasformazioni di coordinate, relative a un’operazione di “riflessione” nello spazio-tempo. Questa confusione viene favorita da un linguaggio assolutamente inadeguato, e perciò mistificante, che include le “riflessioni” nel “gruppo completo delle rotazioni”. Come al solito, da Hilbert in poi, una generalizzazione di natura assolutamente formale viene ad assumere significato fisico per effetto di un abuso di linguaggio! Ecco a che cosa serve quello che Einstein credeva essere “un inutile sfoggio di erudizione matematica”! Ed Einstein niente potrebbe mai obiettare a Minkowski, il quale gli risponderebbe: se vuoi trovare le trasformazioni di Lorentz è inutile complicare le cose con la fisica e con le grandezze; basta assumere che vogliamo trasformazioni “di coordinate” che formino “gruppo” o, equivalentemente, che sia invariante il quadrintervallo; poi, eventualmente, ci sforzeremo di appioppare un qualche significato, più o meno fisico, a quest’ultimo oggetto che è matematicamente ben definito! Fra l’altro, così facendo, daremo un gran lavoro agli inventori di giustificazioni, basterà che non parlino di grandezze fisiche omogeneee, o, se proprio ne vorranno parlare, le identifichino con i numeri di Dedekind; e si limitino a parlare di “esperimenti ideali” fatti con parole e con simboli senza significato fisico, basterà dirli definiti “operativamente”. TORNA

26. Cfr. Il significato della relatività, op. cit. TORNA

27. W. Voigt, Über das Doppler’sche Prinzip, Nachirichten der Königliche Gesellschaft der Wissenschaften zu Göttingen, 10 März 1887. TORNA

28. Gli increduli possono consultare The new Palgrave – A dictionary of economics a pag. 1061. TORNA