Riflessioni sulla didattica della fisica

Angelo Pagano

1.) Premessa

Alcuni giorni fa mi son ritrovato in una riunione di amici, quasi tutti docenti di fisica (o comunque di materie scientifiche) nei licei.

L’argomento principale di discussione era l’angustia dei programmi ministeriali per l’insegnamento delle scienze e l’inedeguatezza dei libri di testo. Giudicati entrambi assolutamente inadeguati per la società odierna.

Interpellato dissi che anche all’università, a mio giudizio, la situazione non era molto più entusiasmante.

Pensavo, infatti, che l’insegnamento e, soprattutto, la ricerca nelle discipline scientifiche, avrebbero dovuto essere indirizzati, principalmente, sulla questione ambientale, che mi pareva e mi pare il problema fondamentale e il più urgente da risolvere oggi, pena la sopravvivenza stessa del genere umano su questa terra.

Con mia grande sorpresa i miei amici mi dissero che non era affatto a questo che essi stavano pensando. Sentivano, invece, la mancanza di adeguate conoscenze sui settori moderni della fisica e citavano, come esempio, la teoria della relatività, che, a loro dire e a giudizio di tutti i più grandi fisici del presente, è la più fondamentale delle teorie fisiche, insieme, naturalmente, alla meccanica quantistica.

Come ho già detto la cosa mi ha sorpreso e mi ha fatto modificare un po’ alcune decisioni che avevo preso qualche giorno prima.

Infatti avevo già maturato l’idea di scrivere qualcosa, per i quaderni di Mondotre, sulla questione ambientale, ma questa esigenza dei miei amici, che essi ritenevano essere molto più diffusa di quanto io potessi ritenere, mi ha fatto cambiare obbiettivo. Tuttavia mi son ripromesso di tornare in un futuro, che spero non molto lontano, sul primo problema.

Io avevo già scritto qualcosa sulla relativit๠ma ho sentito il bisogno di tornare ancora sull’argomento, questa volta sotto la prospettiva didattica.

Spero sinceramente di poter dare un piccolo contributo all’esigenza che sopra ho prospettato; anche se temo di tradire le aspettative dei miei amici, dal momento che non condivido affatto il loro entusiasmo per la detta teoria.

Questo perché mi son convinto, anche e soprattutto attraverso quel po’ di ricerca storica che ho dovuto fare per preparare i due articoli di cui alla precedente nota, che il problema non è solo di inadeguatezza dei libri di testo e dei libri di divulgazione scientifica, anche se scritti da illustri scienziati, i quali, con la scusa di rendere più semplici le cose ad un più vasto pubblico di lettori, si lasciano spesso andare a banali luoghi comuni, assolutamente inaccettabili per chi volesse riflettere solo per un momento, abbandonando per un po’ il reverenziale timore nei confronti dell’autorità del grande scienziato, e volesse meditare un pochino di più sulle conseguenze e sull’utilità di quanto viene impartito a scuola o all’università, al fine di non dare ai giovani l’impressione che la scienza non giovi per capire il mondo che ci circonda, ma solo per far apparire possibili i miracoli.

Qualche giovane particolarmente sensibile potrebbe porsi la domanda: se la scienza non giova a capire, a che giova far scienza?!

Per questo penso che sia urgente ridare all’insegnamento e ad ogni libera espressione del pensiero la più grande dignità.

Forse il problema è anche di intrinseche difficoltà della teoria stessa.

Nel seguito intendo mettere a fuoco alcuni punti che, pur della massima importanza e delicatezza, vengono spesso insegnati e divulgati senza alcun riferimento alla critica intelligente e positiva, che pure vi è stata in passato e che continua a registrarsi nel presente, nei confronti di alcuni problemi connessi con la comprensione della teoria che, lungi dall’essere banali, meriterebbero ancora oggi una particolare attenzione.

La questione può essere posta in questi termini.

Nell’insegnamento della relatività (sia speciale che generale) sovente si forniscono ai discenti delle formule matematiche che vengono presentate come leggi fisiche, senza aver prima introdotto la fondamentale distinzione fra legge e modello. Si afferma, contestualmente, che tali supposte leggi sono verificate sperimentalmente e, a sostegno, si citano taluni esperimenti considerati “fondamentali”.

Non si fa nessuno sforzo per vedere se tali esperimenti non siano anche interpretabili all’interno della teoria newtoniana, che ancora oggi costituisce il primo approccio degli studenti con le teorie fisiche.

Rendendo, così, un cattivo servizio sia all’insegnamento della meccanica newtoniana, che viene spesso banalizzata, che a quello della relatività, che viene, il più delle volte, sprofondata dentro un profluvio di parole incomprensibili, e non solo per i poveri studenti!

2.1.) Un po’ dì cronaca del passato

La teoria della relatività, come in seguito è stata rielaborata, non è più quella che Albert Einstein ebbe a proporre in un famoso suo articolo del 1905.

Essa si è venuta modificando per far fronte, da un lato, alle numerose critiche che ebbe sin dal suo nascere e, dall’altro lato, per sottrarla ai salotti ed ai circoli culturali piccolo borghesi, che se ne erano ìmpadroniti, rimettendola, in qualche modo, nel “sacro tempio della scienza”, secondo i canoni della scientificità di un’epoca che sembra ormai passata.

Come tutte le teorie scientifiche, che si presentano come innovatrici sul piano filosofico, essa ebbe molti oppositori negli ambienti scientifici tradizionali. Mentre, a differenza di quanto oggi si possa pensare, la teoria trovò entusiastici consensi al di fuori del campo della scienza, cioè tra giornalisti, filosofi, circoli culturali ecc..

Il successo delle nuove e sconvolgenti idee, al di fuori degli ambienti che tradizionalmente si sogliono considerare scientifici, fu di tale intensità da provocare persino il giustificato risentimento di eminenti scienziati dell’epoca.

Sono sintomatiche le parole che si possono leggere in un intervento dell’illustre scienziato francese Bouasse sulla rivista Scientia:²

“Quando Fresnel immaginò che l’etere vibrasse come un solido e, grazie a questa ipotesi, fondò l’ottica moderna, la Gazette de France non credette opportuno di informarne il mondo intero.

E quando Faraday mostrò che i dielettrici non sono degli isolanti inerti, proposizione dalla quale scaturì la telegrafia senza fili, il Times non innalzò inni di lode.

Quando, più recentemente, J. J. Thomson propose la sua teoria degli elettroni, rimettendo in causa i fenomeni di conducibilità nei gas, il pubblico non ne fu informato.

Eppure la gloria dell’Einstein uguaglia quella del Carpentier e del Siki Battling. I periodici sono pieni dei suoi ritratti; le belle signore fanno la coda per vederlo; passa da una tourné all’altra come un’attrice e si fa la ressa per incontrarlo. Evidentemente, come si suole dire a Toulouse, ci si trova dinnanzi a un di più o a un di meno!

La ragione di questa gloria, che io credo effimera, risiede nel fatto che la teoria di Einstein non rientra nel quadro delle teorie fisiche: essa è una ipotesi metafisica che, per di più, è incomprensibile; doppia ragione per giustificarne il successo.

Che Bergson, illustre filosofo, parteggi per Einstein, è naturale ma è indifferente al dibattito. Credo che ci sia troppo buon senso in giro per ammettere che in questa materia la sua opinione possa avere il benché minimo valore: non andremo certo a chiedergli di spiegarci a cosa serve una teoria fisica e che cosa da questa ci si deve attendere.

Non siamo particolarmente turbati da quelle galanti manifestazioni di cenacoli culturali, dove un ex primo ministro funge da uscere raccogliendo i biglietti d’invito, mi riferisco all’Illustration dell’Aprile 1922. Gli applausi frenetici di una cotale enorme quantità di incompetenti non aggiungono niente all’accettabilità o meno dell’ipotesi.

Poco importa che matematici ed astronomi la tengano in cosi gran conto tanto da trattarci da beoti o da conformisti piccolo-borghesi, e che finiscano con l’insinuare che siamo buoni solo per la carrozzella e per le chiacchiere inutili.

Tutte queste gentilezze ci lasciano indifferenti perché, alla fine, noi fisici sperimentali, avremo l’ultima parola …”.

Il Bouasse, che a giudizio di Peano,³ “ha il coraggio delle proprie opinioni”, ben dipinge l’atmosfera dell’epoca: euforica accettazione della teoria da parte di quanti nulla avevano a che vedere con il quotidiano lavoro del ricercatore di fisica.

Questa testimonianza viene a confermare quanto ho già avuto modo di notare in precedenza, negli articoli sopra citati, cioè che il successo della teoria di Einstein sia dipeso, in larga misura, dal fatto che l’ambiente socio-economico, agli inizi del ventesimo secolo, era ormai dominato da un paradigma empirista e fenomenologista, che ben si sposava con l’efficientismo economico di un capitalismo sempre più aggressivo.

Ma, naturalmente, Bouasse non fu l’unico ad opporsi contro l’accettazione acritica della teoria della relatività come teoria fondamentale della fisica.

Moltissimi altri illustri fisici criticarono più o meno aspramente la teoria.

Il dibattito tra fautori e detrattori si mantenne a livelli di massima intensità e di grande polemica fino a circa la fine degli anni quaranta. Poi, poco a poco, la polemica scese di tono fino a scomparire quasi del tutto. Forse in seguito alla naturale estinzione fisica dei sostenitori del vecchio paradigma. Lo stesso Planck era dell’opinione che un nuovo paradigma scientifico può solo affermarsi solo quando siano morti i rappresentanti della filosofia precedente.

Il lettore che volesse farsi un’idea più precisa delle idee salienti che circolavano intorno alla “questione relativistica” negli anni 1920-1930 può consultare i fascicoli della rivista Scientia a partire dall’anno 1923. Vi si possono rintracciare le opinioni dei più famosi scienziati dell’epoca (quali Fabry, Somigliana, Castelnuovo, Eddington, Levi-Civita, La Rosa, Fubini e tanti altri ancora), ai quali la rivista aveva offerto esplicitamente l’occasione di esprimere liberamente le loro opinioni in merito.

2.2) La didattica della relatività

Quando per la prima volta lessi il libro dell’illustre prof. Eligio Perucca, già famoso docente dell’Università di Torino, fui colpito dalla mancanza, in quella pur ponderosa opera, di un capitolo riguardante la moderna teoria della relatività.⁴

Una tale mancanza fu giudicata gravissima, sin dalla pubblicazione della prima edizione, da parte di colleghi ed allievi del Perucca. L’autore nella prefazione alla seconda edizione scrive testualmente:

“Dei suggerimenti, dei benevoli appunti di Colleghi e Lettori ho fatto tesoro. Ma non ho potuto, ad esempio, accogliere l’amichevole consiglio, rivoltomi da un mio caro e chiaro Collega, che avrebbe voluto un posto per la Meccanica relativistica nel mio trattato. Evidentemente il mio amico e Collega volle attribuire al mio libro una portata che l’autore, pur nella sua immodestia, non osò assegnargli. Perciò il mio libro si rinnova senza Relatività.”

Queste parole mi sembrano assai significative e, a mio giudizio, forse non dicono tutto.

In effetti, il libro del Perucca, a differenza della generalità dei più moderni libri di fisica generale, finalizzati esplicitamente all’insegnamento, dedica ampio spazio alla metrologia.

In quelle pagine si può apprendere con profitto l’arte “di misurare” con accuratezza e precisione; arte che dovrebbe essere il bagaglio naturale del fisico.

La teoria delle grandezze fisiche è ivi espressa con tale chiarezza da non lasciare dubbi sul perché l’autore, a mio avviso, non può trattare la teoria della relatività.

Questa infatti fonda tutta la sua brillante forza persuasiva col lavorare con dei simboli che non possono, in alcun modo, rappresentare delle grandezze, secondo la definizione del Perucca; la quale, del resto, coincide con quella universalmente concepita dai fisici sperimentali.

In breve, credo di poter dire che la relatività non sta nel libro del Perucca semplicemente perché non ci può stare, a prescindere dal fatto che l’autore potesse considerare qualche formula della teoria come valida relazione di natura fenomenologica.

Il suo inserimento avrebbe richiesto la cancellazione automatica, ma anche paradossale, della teoria delle grandezze fisiche che, è bene ribadirlo, non è fisica “classica” o “quantistica” o “relativistica”; ma, se così mi è permesso dire, è al di sopra di qualsiasi teoria o paradigma. Essa rappresenta l’essenza stessa della fisica, strumento irrinunciabile per la conoscenza sperimentale.

Ma cosa è una grandezza fisica?

Seguiamo il Perucca:

“Grandezza fisica è ogni ente utile per la descrizione dei fenomeni fisici e suscettibile di definizione quantitativa, cioè di misurazione”.

Quando si rifletta un poco e ci si accordi sul significato da attribuire al concetto di misurazione, si può dire che un ente, diciamolo a, è una grandezza se, presa ad arbitrio una quantità numerica, diciamola q, si ha che il prodotto q ´ a (che significa: si prenda q volte a) è ancora una grandezza, che, p. es., chiameremo b.

Il numero q si dice misura o valore di b rispetto ad a.

“Grandezza fisica” è il nome di una classe.

Uno qualsiasi dei suoi membri può essere preso, ad arbitrio, per misurare un’estensione. La scelta della grandezza unità è un fatto di pura convenienza e comodità.

Questa definizione di grandezza, già nota ai pitagorici, è con chiarezza espressa da Euclide e da Archimede.

Dai postulati fondamentali della teoria delle grandezze discende che queste godono della proprietà dell’“additività”, allo stesso modo delle quantità numeriche.

Siano a, b, due grandezze omogenee tra loro (cioè tali che sia possibile determinare una quantità numerica q in modo che si abbia a = q ´ b); siano q_a , q_b , le loro rispettive misure, relativamente alla grandezza unitaria u; o, in simboli, sia a = q_a ´ u e b = q_b ´ u ; sia α una quantità numerica (numero reale), si può definire il prodotto della grandezza fisica per il detto numero ponendo: α ´ a uguale alla grandezza che si ottiene facendo α q_a ´ u (dove tra α e q_a è sottinteso il segno del normale prodotto tra numeri).

Si definisce, invece, la somma c = a + b ponendo c = (q_a + q_b) ´ u (dove la somma tra numeri si intende nota).⁵

Le grandezze dunque rappresentano un esempio di quello che i matematici definiscono astrattamente come “spazio lineare”, anzi ne è l’archetipo.

Esempi di grandezze fisiche sono: la massa, la carica, il tempo, la lunghezza, l’energia, la quantità di moto, ecc.

Ora, se si accetta l’interpretazione che oggi viene data delle formule relativistiche, sarà necessario ammettere che gli enti con cui si opera in relatività non godono della proprietà di additività, la quale caratterizza le grandezze fisiche. Esempi ne sono la massa relativistica di un corpo e la sua velocità.

Soffermiamoci un momento sul concetto di massa di un corpo.

Il Landau nel suo famosissimo e diffusissimo libro di fisica teorica⁶ afferma che:

“…mc² non è uguale alla somma Σ_a m_ac² (m_a sono le masse delle particelle) e, di conseguenza, nemmeno m è uguale a Σ_a m_a. Quindi nella meccanica relativistica la legge di conservazione della massa non sussiste: la massa di un corpo composto non è uguale alla massa dei suoi componenti…”.

Ovviamente analoghe affermazioni si ritrovano per la velocità, il tempo e così via.

Se si accetta l’interpretazione del Landau (che comunque, è bene precisarlo, è la stessa di quella che viene data dalla maggior parte dei libri di testo) si è costretti ad ammettere che o la massa relativistica non è una grandezza fisica oppure che la massa di cui si parla in relatività è solo l’“apparenza della massa”, per usare il linguaggio parmenideo.

La prima ipotesi porterebbe la relatività immediatamente fuori dal quadro delle teorie fisiche. La seconda ipotesi porterebbe a giustificare la validità empirica di certe formule della relatività, nel dominio di certi fatti sperimentali, come semplice manifestazione di particolari correlazioni tra grandezze, tra le quali, ma non necessariamente, vi possono essere le masse come intese da Newton, cioè come quantità di materia.

Tali correlazioni si manifestano in dipendenza delle particolari operazioni fisiche che facciamo per misurarle. La relatività verrebbe ridotta a pura “fenomenologia”, eventualmente in grado di riassumere una, più o meno grande, collezione di fatti. Dunque essa si risolverebbe in tassonomia, cioè semplice “classificazione” di fatti e non potrebbe pretendere di fornire una “spiegazione” del mondo fisico.

Da questo punto di vista, la teoria di Einstein si piazzerebbe più nella tradizione della fisica scaturita da Platone e da Aristotele piuttosto che in quella tradizione di filosofia naturale che scaturisce da Pitagora e Democrito.⁷

È bene avvertire che la “fenomenologia” può risultare estremamente utile, e possibilmente anche sufficiente, per le applicazioni pratiche della conoscenza scientifica (tecnologia); ma tradirebbe, presa da sola e in sostituzione, gli scopi stessi della scienza come intesa dagli antichi scienziati, cioè come “filosofia naturale”.

La quale ultima, quanto meno, ha sicuramente maggior valore euristico della pura fenomenologia e rappresenta la molla essenziale per il progresso della scienza, con lo stesso grado, ma con insostituibile ruolo, col quale la fenomenologia costituisce lo strumento essenziale per lo sfruttamento della scienza.

Parlando di relatività non si può fare a meno di citare il punto di vista del Bridgman, che viene considerato il padre dell’operazionismo moderno:⁸

“La relatività ristretta di Einstein ha dato un grande contributo nel raggruppare e coordinare i fenomeni in modo che essi possano venire abbracciati tutti da una formula matematica semplice, ma non sembra averli presentati sotto una luce tale che sia semplice o facile coglierli fisicamente. L’aspetto esplicativo manca del tutto nel lavoro di Einstein ...”.

Ma ora soffermiamoci su alcuni punti particolari, sui quali la critica è stata più sensibile nel passato.

2.3) Energia e massa

Analizziamo per prima la questione della massa relativistica un po’ più in dettaglio.

Scegliamo ancora il Landau come libro di riferimento, anche perché è ritenuto uno tra i migliori libri di testo esistenti.⁹

Partiamo dalla famosa formula della relatività speciale valida per una particella non soggetta a forze:

(2.3.1) .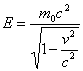

In essa c è la velocità della luce, v è la velocità della particella, m₀ viene chiamata la “massa a riposo” del corpo, E sarebbe l’energia totale della particella che, per v = 0, diventa l’energia a riposo E= m₀c².

È istruttivo vedere come gli autori sopra citati pervengono a tale risultato.

Sotto opportune ipotesi, che gli autori richiedono per il momento di accettare, viene ricavata l’espressione della “lagrangiana relativistica”, come applicazione del principio di minima azione; quindi si scrive:¹⁰

,

con il parametro α caratteristico della particella data.

La dimostrazione della formula (2.3.1) procede come di seguito qui indicato.

Poiché, in meccanica classica, la particella è caratterizzata dalla sua massa m₀ bisogna trovare il legame tra α ed m₀. Per trovarlo si imponga la condizione che al limite per c tendente all’infinito si debba ottenere la lagrangiana classica .

Sviluppando in serie la lagrangiana relativistica si ha:

.

A questo punto è bene rifarsi direttamente alle parole del libro:

“Come si sa i termini della funzione di Lagrange che rappresentano una derivata totale rispetto al tempo non sono essenziali e li si può omettere. La costante che compare nello sviluppo si può dunque omettere nell’espressione di L.” (Si faccia attenzione a quest’ultima frase perché la più importante per il nostro discorso).

Avendo trascurato la costante, per ottenere l’espressione classica, basta porre α = m₀c e si ottiene:

,

che è l’espressione cercata per la lagrangiana.

A questo punto, seguendo l’impostazione analitica che gli autori hanno dato al loro corso sin dal primo volume, si determina l’impulso, p, della particella libera a partire dalla definizione e si trova:

.

E, allo stesso modo, definendo l’energia secondo l’espressione:

,

ed eseguendo i facili calcoli si trova l’espressione (2.3.1) per l’energia della particella libera.

Se si pone v = 0 si deve ottenere l’energia a “riposo” della particella:

(2.3.2) E = m₀ c²

Ma si dimentica, ed è quanto qui volevo far notare, che la lagrangiana era stata definita a meno di una funzione arbitraria del tempo e dunque, per lo meno, a meno di una costante (cosa che, del resto, gli autori ci avevano, opportunamente, fatto notare quando avevano voluto ottenere il limite classico).

Se dunque riteniamo che la lagrangiana è determinata a meno di una costante, chiamiamola k, ponendo k = - m₀ c², possiamo ottenere E= 0; ponendo k = - 2 m₀ c² otterremo, invece, E = - m₀ c² e così via di seguito potremo ottenere tutti i valori che vogliamo.

Ma la “piccola” omissione del Landau si propone effetti sconvolgenti. Infatti, come si potrebbe altrimenti insegnare agli studenti, e futuri insegnanti, che “la massa a riposo di una particella misura la quantità totale di energia ivi contenuta”?!

Per le ipotesi fatte la sola cosa che si può asserire è:

Δ E = Δ mc²

e ci resta ancora da sapere che cosa significhi Δ m. Certamente non può essere la variazione di quantità di materia, newtonianamente intesa; ma può ben essere una variazione di massa inerziale, che è cosa ben diversa dalla prima, come il banale esempio di una sfera che rotola su di un piano inclinato mette in mostra.

Il lettore a questo punto obietterà che non bisognerebbe essere eccessivamente formalisti, poiché il “piccolo imbroglio” è giustificato dall’esigenza di rendere semplice la dimostrazione di una legge che, soprattutto nel campo della fisica nucleare, ha ottenuto numerose evidenze sperimentali. (Ma a che servono le dimostrazioni che non dimostrano?!)

Infatti la formula espressa dall’eq. (2.3.2) conduce naturalmente al teorema (detto, molto spesso, “principio”) di equivalenza massa energia, che si ritiene ampiamente provato dall’esperienza, anche tragica (penso alla bomba atomica).

Come si sa, non vi è nulla di più arduo che combattere le “evidenze di fatto”. Il lettore segua il ragionamento che di seguito espongo e poi giudichi senza pregiudizi.

Consideriamo, all’interno dello schema newtoniano, un corpo pensato come un insieme di n particelle elementari (cioè piccoli corpi idealizzati come punti massa) interagenti tra loro, e supponiamo che non vi siano forze esterne.

L’energia totale del corpo è:

E = T + U

con T l’energia cinetica e U l’energia potenziale; o, più esplicitamente:

(2.3.3) ,

con: U_{i j} = U_{j i} , ma U_{i j} = 0 per i=j .

Introducendo la velocità, V (V² =V²), del baricentro del sistema, potremo separare l’energia cinetica macrosopica del corpo dall’energia cinetica interna:

(2.3.4) ;

dove abbiamo indicato con la massa totale del corpo.

Indichiamo con E_int = T_int + U, l’energia totale interna del corpo e definiamo la grandezza , che chiameremo “massa efficace” del corpo.

L’energia totale diventa:

(2.3.5) E = T_corpo + mc² .

Ci proponiamo ora di determinare il guadagno (o perdita) di energia cinetica macroscopica che si potrebbe ottenere da un processo di scissione di un corpo A in due corpi B e C (A ® B + C).

Applicando la (2.3.5) otteniamo:

(2.3.6) T_A + m_A c² = T_B + m_B c² + T_C + m_C c² ;

e dunque:

(2.3.7) D T = (T_B +T_C) - T_A = [(m_B +m_C) - m_A] c² .

Supponendo di aver misurato le masse efficaci in gioco (o di conoscerle in base a un qualche opportuno modello), possiamo ottenere facilmente il guadagno di energia cinetica macroscopica della “reazione”.

Da questo esempio possiamo concludere che, all’interno dello schema newtoniano, sarebbe possibile spiegare un processo di fissione nucleare. Allora il problema sarebbe solo quello di verificare sperimentalmente se tali variazioni di energia cinetica macroscopica sono esattamente quelli previsti dalla relazione massa energia relativistica.

I primi esperimenti ideati per la “verifica sperimentale” dell’equivalenza massa energia, furono riportati nel 1933 da K. I. Bainbridge.¹¹

Nel suo articolo vengono discussi gli esperimenti di (a) Cockcroft - Walton e di (b) Lewis - Livingston - Lawrence.

Il primo esperimento, (a), consisteva nel bombardamento di bersagli di Litio 7 con protoni (nuclei di idrogeno) con un’energia¹² incidente di 270 K eV. Come risultato di questi bombardamenti si osservavano, in uscita, due particelle alfa che percorrevano una distanza in aria di 8.4 cm. In base al percorso delle particelle si stimava che esse dovevano possedere un’enegia cinetica di 8.6 M eV.

Si supponeva di descrivere il processo considerato con l’equazione simbolica:

¹H + ⁷Li ® α + α .

Moltiplicando per due l’energia della particella alfa e sottraendone l’energia cinetica del protone incidente, veniva stimato un guadagno di energia cinetica pari a 16.9 M eV.

Applicando la relazione di equivalenza massa energia D E = D mc² e supponendo noto il valore della costante c (che nell’articolo non viene dato) si stimava una differenza di massa di 0.0182 unità di massa (nella scala basata sull’ ossigeno 16).

Si accettavano i valori sperimentali delle masse del protone e della particella alfa come dati da Aston (che, però, non vengono indicati)¹³ e quella del litio come data dallo stesso Bainbridge (7.0146 ± 0.0006); si otteneva una differenza di massa di 0.018 che veniva giudicata in “soddisfacente accordo” con le predizioni della formula relativistica di equivalenza massa energia.

Il secondo esperimento (b) riguardava il bombardamento del Litio 6 con deutoni (nuclei di deuterio). In questo caso si osservavano due particelle alfa di “percorso” differente: 8.2 cm e 14.8 cm, rispettivamente. L’energia incidente era di 1.33 M eV.

Anche in questo caso si stimava l’energia delle particelle alfa mediante i loro percorsi. Tuttavia, in base ai dati sperimentali disponibili, veniva determinata l’energia della particella alfa di maggiore percorso, il cui valore era dato in 12.5 M eV. Assumendo il processo di disintegrazione

⁶Li+ ²H ® α + α

e, supponendo valida la legge di conservazione dell’impulso, si calcolava un guadagno in energia di 23.7 M eV. Applicando l’equivalenza massa energia anche in questo caso, si otteneva un differenza di massa di 0.025. Assumendo i valori delle masse di Aston (per le alfa) e di Bainbridge (per il Litio), si calcolava, in questo caso, una differenza di massa di 0.023, che veniva giudicata, questa volta, “in non soddisfacente accordo” con la relazione di equivalenza massa energia. Il Bainbridge, a conclusione dell’articolo sottolineava che, per verificare meglio il “disaccordo”, sarebbe stato necessario effettuare un test più stringente, ammesso che fosse stato possibile avere una più precisa relazione empirica tra energia cinetica e “percorso delle alfa”.

A parte il fatto che, come abbiamo visto sopra, la validità della relazione di equivalenza massa energia può solo essere confermata con un errore massimo stimato non minore dell’8%, notiamo che ci si trova di fronte a due esempi che dovrebbero, in teoria, corrispondere alle condizioni ideali richieste per l’applicazione della relazione di equivalenza in esame.

Tutti gli altri esempi di questo tipo che si potrebbero portare, anche i più recenti, si prestano alle stesse critiche.

In tali esperimenti si cerca la variazione di energia cinetica del moto dei baricentri dei corpi (nuclei) mediante la conoscenza delle loro masse, come determinate empiricamente, tramite un processo di misurazione, che concisamente chiameremo O_m.

Ora, se si verifica che differenti operazioni del tipo O_m danno differenti valori di m, ciò significa, dal punto di vista operativo, che la “massa” che si misura non è una grandezza fisica associata al corpo in esame ma dipende in modo essenziale dalle operazioni fisiche che bisogna compiere per determinarla. Operazioni diverse potrebbero dare valori diversi. Per esempio, per il difetto di massa del protone, ¹H, si danno i seguenti valori:¹⁴

[8.130 - Mattauch (1940)], [8.128 - Cohen et al. (1947)], [8.128 - Bainbridge (1948)], [8.169 - Roberts (1951)], [8.141 - Ewald (1951)], [8.146 - Collins et al. (1951)], [8.142 - Li et al. (1951)].

Un’analisi degli errori più probabili (che qui si omette per brevità, rimandando al libro dell’Evans) con cui i diversi autori dicono di poter determinare le tre cifre significative dopo il punto, rivela che, come dice l’Evans, “i valori più probabili sono spesso mutuamente inconsistenti, e di molte volte l’errore probabile ad essi assegnato” ed, ancora, che “queste incertezze vanno fuori l’errore probabile assegnato sulla base della riproducibilità statistica dei risultati. Esse (incertezze) sono dunque dovute ad errori sistematici sconosciuti relativi alla particolare tecnica usata”.

Analoghe osservazioni valgono per le masse del litio, deuterio, elio, e di tutti gli elementi conosciuti.

Non migliore, o addirittura peggiore, sembra essere la situazione in altri campi dove si arriva ai valori delle masse, a partire dai dati sperimentali, attraverso l’intermediazione di poco controllabili approssimazioni, sulla base della teoria quanto - relativisica dei campi.

È chiaro dunque che le verifiche sperimentali dell’equivalenza tra massa ed energia, come quella illustrataci dall’esperimento del Bainbridge, dipendono in larga misura dagli effettivi valori usati per le masse. Per lo stesso sistema si può dichiarare un “soddisfacente accordo” oppure un “non soddisfacente accordo” dal momento che non è per niente chiara l’origine di quelli che Evans chiama “errori sistematici sconosciuti”.

Dal punto di vista dell’analisi newtoniana, che sopra abbiamo schizzato, tale origine sconosciuta potrebbe risultare, invece, molto chiara. Infatti il difetto di massa Δ m verrebbe a dipendere dalle particolari configurazioni interne dei nuclei. A parte i disturbi apportati al sistema atomico nel suo complesso (nuclei ed elettroni) che sono sicuramente non trascurabili e dello stesso ordine di grandezza di Δ m.

Dalle precedenti considerazioni si può concludere che le masse, di cui si parla in fisica nucleare, non sono certamente le quantità di materia, newtonianamente intese, bensì delle masse efficaci. Questa supposizione è resa ancor più plausibile se riflettiamo sul modo con cui esse vengono determinate.

Una rilevante quantità dei valori delle masse tabulati sono stati ricavati facendo uso della formula di equivalenza massa energia (per es., il valore di 8.142, già citato e dovuto a Li et al.). Dunque devono essere considerate delle masse efficaci che non possono valere come conferma dell’equivalenza; che, tuttavia, innescano un processo a circolo chiuso, cioè tautologico, e non si verrebbe più a capire se la relazione massa energia è una legge fisica o una semplice definizione, banalmente vera per necessità logica.

Alcuni valori di massa vengono ottenuti con metodo diretto, sfruttando l’azione combinata di campi elettrici e magnetici.

Un atomo di carica q viene accelerato mediante una differenza di potenziale e si scrive l’equazione per l’energia cinetica:

(2.3.8)

successivamente, il sistema atomico viene sottoposto all’azione di un campo magnetico H e si impone l’uguaglianza fra forza di Lorentz e forza centrifuga:

(2.3.9) ,

essendo R il raggio di curvatura e B = μ H l’induzione magnetica.

Dalle misure di , B, R si ricava il rapporto, dal quale, supponendo noto il valore di q, si ottiene m. La teoria degli esperimenti è, in effetti, molto più complicata di quella qui delineata. Ma l’essenza è data dalle formule (2.3.8 e 2.3.9).

Quello che qui voglio sottolineare è il fatto che, nello sviluppo della teoria, anche in questo caso, si trascurano completamente i moti interni del sistema atomico, le sue dimensioni e la sua forma, supponendoli ininfluenti, il che equivale a trattare il sistema atomico come un punto massa.

Questo, classicamente, può essere fatto solo sotto opportune ipotesi sulle forze esterne (loro eventuale riducibilità ad un’unica forza agente nel baricentro, ecc.) e sotto opportune altre ipotesi sulla struttura dei legami interni (se corpo rigido oppure no, ecc.).

In base a quanto detto, è chiaro che le misure di massa eseguite con strumenti che usano le filosofie sopra illustrate danno una massa che non necessariamente è la somma delle masse dei costituenti; e un’analisi classica potrebbe rendere conto delle frequenti deviazioni che invece vengono attribuite a non spiegati errori sistematici.

Le prove sperimentali che si portano a favore dell’equivalenza massa energia difficilmente possono essere considerate come necessariamente a favore della teoria relativistica e, in ogni caso, non possono contraddire la teoria newtoniana.

2.4) La luce ed il campo elettromagnetico

Come oggi è dai più riconosciuto, la relatività di Einstein non nacque da esigenze di carattere sperimentale, ovvero da fallimenti della teoria newtoniana, presunti o reali che essi siano. Ma, piuttosto, essa ripone le sue origini nell’esigenza di conciliare le nozioni di spazio e di tempo che sembrano essere diverse quando si passa dalla meccanica newtoniana alla teoria elettromagnetica di Maxwell - Lorentz.

Einstein crede di individuare nella teoria elettromagnetica, piuttosto che nella teoria newtoniana dei corpi, il cardine fisico e filosofico per l’interpretazione del mondo fisico.

Leggiamo ancora uno stralcio tratto dal libro di Bridgman:¹⁵ “Praticamente tutto il nostro pensiero intorno ai fenomeni ottici si impernia su un’invenzione, mediante la quale questi fenomeni vengono assimilati a quelli dell’esperienza meccanica ordinaria e così resi più accessibili all’intelligenza…

…Dal punto di vista operativo è privo di senso l’attribuire una realtà fisica alla luce nello spazio intermedio (cioè tra sorgente e rivelatore) e bisogna riconoscere che la luce come cosa che viaggia è soltanto un’invenzione…

…Questa idea della luce è fondamentale in tutto lo svolgimento della relatività ristretta”.

In effetti se si analizza l’opera dell’Einstein, indipendentemente dalle possibili deviazioni interpretative, si deve concordare con il Bridgman che Einstein ha in mente l’idea di un campo come substrato reale a cui ricondurre persino il significato di corpo o di massa.¹⁶

Per Einstein la luce è qualcosa che viaggia e non è un semplice modello. Egli crede che le equazioni del campo elettromagnetico di Maxwell siano “Le Leggi” per antonomasia. Ciò è confermato dallo stesso¹⁷ quando, rispondendo alle critiche ricevute sul ruolo preminente che la velocità della luce assume nella sua teoria, asserisce che la luce è il fenomeno che meglio conosciamo, grazie alle indagini di Maxwell e Lorentz.

Questo punto di vista, certamente “metafisico”, intorno al significato da attribuire alle equazioni di campo, lo condurrà naturalmente ad assegnare alle trasformazioni di Lorentz un’importanza fondamentale, molto al di là di quella che, molto più modestamente, tali trasformazioni sembrano indicare.

Per capire meglio la questione è bene ricordare, brevemente, il significato delle cosiddette equazioni di Maxwell - Lorentz.

Maxwell propose le sue equazioni come riassunto delle leggi empiriche, e quindi macroscopiche, dell’elettromagnetismo. Per ragioni di pura simmetria formale e assumendo la conservazione locale della carica elettrica, introdusse una nuova grandezza fisica, che si usa chiamare corrente di spostamento. Tale ipotesi fisica apre il campo alle radioonde (brillantemente confermate dagli esperimenti di Hertz); ma, cosa più importante dal punto di vista teorico, unifica i fenomeni ottici con quelli elettromagnetici; per cui la velocità della luce, usualmente misurata “cinematicamente”, viene ad essere legata in modo univoco alle costanti dell’elettricità e del magnetismo. Questo permette una misura “statica” di c. (In effetti, l’accordo tra i due tipi di misurazioni non è così buono rispetto a quello che si potrebbe pretendere data la precisione con la quale tali misure possono essere eseguite. Anche su questo punto ci sono state e ci sono contestazioni).

Tali equazioni fenomenologiche non sono invarianti per le cosiddette trasformazioni di Galileo, a differenza delle equazioni di Newton, come si scrivono in un riferimento assoluto.

Ma, finché le equazioni di Maxwell si interpretano come leggi macroscopiche, non si vede nessun problema in questo fatto; nessuno può pretendere che le medie statistiche si debbano comportare come le grandezze microscopiche.

L’idea di interpretare microscopicamente le equazioni di Maxwell si deve a Lorentz, il quale fra l’altro nella sua teoria dell’elettrone è il primo a ricavare le equazioni macroscopiche da quelle microscopiche.

Per far questo deve fare parecchie approssimazioni. Oggi la critica che viene fatta a tale derivazione è che: si parte da equazioni che sono invarianti per trasformazioni di Lorentz, e quindi sono “relativistiche”, si procede poi “non relativisticamente” e quindi si deve imporre “per postulato” che quelle macroscopiche siano in accordo con le trasformazioni di Lorentz.¹⁸

A questo punto le equazioni di Maxwell, interpretate microscopicamente, non sono più delle leggi fenomenologiche, ma diventano “principi fondamentali” della fisica e si pone il problema della loro compatibilità con i “principi altrettanto fondamentali” della meccanica.

Si è creduto e si crede che l’esperimento di Michelson - Morley neghi la possibilità di “spazi” diversi per i fenomeni elettromagnetici e per i fenomeni meccanici. Per cui le ipotesi relativistiche di Einstein sono la sola ancora di salvezza.

Indipendentemente dalla validità e dal significato dell’esperimento di Michelson-Morley, che discuteremo in seguito, c’è, primariamente a nostro giudizio, da chiedersi: è vero che le equazioni che descrivono i fenomeni meccanici debbano sempre essere invarianti per trasformazioni di Galileo?

Su questo punto ci possono essere parecchi dubbi! Daremo ora un esempio, che qualche volta viene riportato sui libri di testo, ma senza menomamente accennare alla sua connessione con il problema che stiamo esaminando.

L’equazioni di Maxwell-Lorentz modernamente si scrivono (nel sistema di Gauss razionalizzato) così:¹⁹

(2.4.1)

(2.4.2) div B = 0

(2.4.3)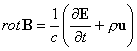

(2.4.4) div E = ρ

dove c è una costante avente le dimensioni di una velocità, nota come “velocità della luce nel vuoto”, e ρu è il vettore densità di corrente definito come il prodotto tra la densità di carica e la sua velocità (in effetti, in uno schema microscopico, è una somma di singolarità).

Si postula l’equazione di continuità:

(2.4.5) .

Le relazioni (1-4) viste come equazioni nelle incognite E e B, con le assegnate funzioni ρ e u, e sotto opportune condizioni, sono risolvibili univocamente.

Noto il campo elettromagnetico E, B in tutto lo spazio, l’equazione del moto di una particella di massa m e carica q sufficientemente piccola, tale da non alterare il campo già dato, si scrive mediante la consueta forza di Lorentz:

(2.4.6)

essendo p,v, rispettivamente, impulso e velocità della particella soggetta al campo di forze.

Si può far vedere che le relazioni formali di cui sopra si possono scrivere anche nell’ambito della teoria classica delle particelle.

Si consideri un sistema di riferimento S rispetto al quale valgano le tre leggi della dinamica di Galileo-Newton.

Supponiamo data una distribuzione di cariche di densità ρ funzione di punto e supponiamo che questa distribuzione sia fissa nel riferimento S; sia il potenziale newtoniano associato. L’equazione del moto di una particella di massa m e carica q si scrive allora:

(2.4.7) ;

si ha (teorema di Gauss):

(2.4.8) div grad = ρ .

Se in luogo del sistema S consideriamo il sistema di riferimento S ′ , che si trovi in moto rotatorio rispetto ad S, l’equazione del moto acquista la forma:

(2.4.9) ,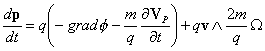

dove V_P e Ω hanno i ben noti significati di velocità di trascinamento e di velocità angolare, per le quali si ha:

(2.4.10) V_P = Ω Ù r

(2.4.11) rot V_P = 2Ω ,

dove r = P — O è il raggio vettore di P rispetto ad un punto fisso in S sull’asse di istantanea rotazione.

Definiamo:

(2.4.12)

(2.4.13)

(2.4.14)

(2.4.15) B = rot A ,

la costante arbitraria c ha le dimensioni di una velocità; ed A si possono chiamare, in analogia alla teoria dei campi, potenziali, rispettivamente, scalare e vettore.

Queste posizioni ci permettono di scrivere in forma più concisa l’equazione

(2.4.9):

(2.4.6′) ,

che possiamo chiamare forma di Lorentz delle equazioni del moto della particella, in un campo di forze come visto dal sistema S ′. Inoltre, dalle definizioni (2.4.13) e (2.4.14), tenendo conto delle proprietà degli operatori rot e div si ottiene:

(2.4.1′)

(2.4.2′) div B = 0.

Applicando l’operatore div alla (2.4.14) si ottiene:

;

e notando che:

(2.4.16) div V_P = div (Ω Ù r) = r × rot Ω - Ω × rot r ,

con

(2.4.17) rot Ω = 0 ,

supponendo Ω indipendente da P. D’altra parte:

rot r = 0 ;

e, infine, si ottiene:

(2.4.4′) div E = ρ .

Derivando l’espressione (2.4.4′) rispetto al tempo si ha:

.

Ammettiamo che l’osservatore solidale con S ′ scriva 1’equazione di continuità (2.4.5) per il moto apparente della distribuzione di cariche che egli giudica in moto.

Con questa ipotesi di carattere fisico l’ultima equazione si scrive:

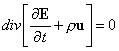
Questa relazione ci dice che si può porre:

(2.4.3′) .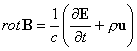

Si è così mostrato che equazioni della stessa forma di quelle Maxwell si possono scrivere all’interno dell’usuale meccanica classica delle particelle interagenti. Esse, in questa luce, rappresentano espressioni formali a cui devono obbedire i campi delle forze d’inerzia che si originano nei sistemi ruotanti rispetto ad un sistema considerato come inerziale.

Notiamo che le definizioni introdotte si prestano bene per altre interessanti estensioni. Per esempio, si può vedere che, ridefinendo i potenziali scalare e vettore nella forma:

con f funzione arbitraria, si perviene alla cosiddetta “invarianza di gauge” per i potenziali.

Si potrebbe, ancora, rimuovere l’ipotesi che Ω dipenda solo dal tempo introducendo una funzione di campo (basterebbe introdurre un operatore lineare, simile a quello che si introduce nel trattare le “deformazioni rigide” di un mezzo continuo), ma questo ci porterebbe lontano dagli scopi che mi sono prefisso, che consistevano nel mostrare semplicemente che l’invarianza galileiana non è obbligatoria neanche nella teoria classica delle particelle. D’altra parte, nessuno ci assicura che il sistema delle stelle fisse sia inerziale, anche se si fa usualmente tale ipotesi; e, in ogni caso, non è detto che lo sia rispetto al baricentro delle cariche elettriche dell’universo.

2.5) Le trasformazioni di Voigt - Lorentz

Come è noto dalle equazioni di Maxwell si deduce facilmente l’equazione delle onde, valida anche in tutti i fenomeni lineari della meccanica classica dei mezzi continui, come in acustica, in idrodinamica, ecc.

Essa per tre coordinate arbitrarie x, y e z si scrive:

(2.5.1)

dove ‘P può rappresentare una vibrazione in un mezzo elastico.

L’eq. (2.5.1) è la rappresentazione matematica di un modello del continuo che riesce a descrivere molti fatti osservati. Per esempio, in meccanica classica (newtoniana) la si stabilisce agevolmente per descrivere la propagazione delle onde sonore nell’aria e, nel caso unidimensionale, l’onda che si propaga su di una corda di violino, ecc..

In tal caso, è l’ascissa lungo la direzione di propagazione, e ct è il tempo misurato in unità di lunghezza, ottenuto moltiplicando il tempo per la velocità (di fase) di propagazione delle vibrazioni sulla corda.

Ma l’eq. (2.5.1), come è noto, descrive anche il fenomeno di propagazione di onde elettromagnetiche nel vuoto o in mezzi isotropi.

Ci troviamo dunque di fronte ad un modello matematico che descrive situazioni fisiche differenti tra loro come, p. es., le “oscillazioni meccaniche” di un mezzo e le “oscillazioni elettriche”.

L’equazione (2.5.1) ammette come soluzione generale:

(2.5.2) Ψ (x, y, z, t) = f (r + ct)+g (r - ct) ,

dove f, g sono funzioni arbitrarie degli argomenti (r+ct) e (r - ct) ed . Se introduciamo le nuove variabili x′, y′, z′, t′ legate alle precedenti da una trasformazione, tale che si abbia:

(r + ct) = h₁(r′ + ct′)

r - ct = h₂(r′ - ct′)

con h₁, h₂ funzioni arbitrarie dei nuovi argomenti e sostituiamo nella soluzione generale si ha:

Ψ (r′ , ct′) = f (h₁(r′ + ct′)) - g (h₂(r′ - ct′))

che, ovviamente, è ancora una soluzione della nostra equazione. Un caso particolare di tali trasformazioni è quello lineare:

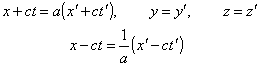
con a costante diversa da zero.

È facile verificare che si ha, in questo caso:

r² - c² t² = r′ ² - c² t′ ² .

Riconosciamo subito che la trasformazione indicata ha tutte le caratteristiche di una trasformazione di Lorentz, basta porre e :

x = γ(x′ + βt′) y′ =y z′ = z

c t= γ (β x′ + c t′).

Questo risultato era già da tempo noto, prima dell’avvento della relatività e prima ancora dei classici lavori di Lorentz sulla dinamica dell’elettrone, per cui tali trasformazioni, da alcuni, sono giustamente chiamate “trasformazioni di Voigt-Lorentz”.²⁰

Infatti, questi risultati e molti altri, che ormai vengono considerati come semplici “curiosità storiche”, fanno parte di un vasto e competente lavoro, condotto dal Voigt intorno al 1880.²¹

Il Voigt dedusse tali trasformazioni come le uniche che permettono ad un’onda sferica, che si propaghi in un mezzo, di essere vista ancora come sferica, con lo stesso raggio, da un osservatore in moto rettilineo uniforme rispetto al mezzo, con velocità . Ma, probabilmente, erano solo una curiosità matematica, non realizzabile fisicamente.

Infatti, di tutti i modi equivalenti conosciuti, per giungere a tali trasformazioni, nessuna può essere compatibile con la teoria delle grandezze.²²

Elenchiamo tali modi di derivazione (vedi il riferimento citato a nota 20):

1) Le trasformazioni che lasciano invariata l’equazione dell’onda in uno spazio tridimensionale (von Laue).

2) Le trasformazioni che lasciano invariato il quadrintervallo r² — c²t² (Minkowski).

3) Le trasformazioni che lasciano invariata una rotazione immaginaria, ponendo x₀ = ict (Marcolongo).

4) Le trasformazioni che lasciano invariata (in forma e in volume) un’onda sferica propagantesi in un mezzo, per una traslazione uniforme di velocità assegnata (Le Roux).

5) Le trasformazioni lineari che formano gruppo, avendo già accettato i due postulati di Einstein (Pauli).

Poi ci sono le derivazioni che non sono derivazioni, come nella maggior parte dei libri di testo.²³ Qui si parte dall’unica affermazione che si può fare assumendo il principio detto della costanza della velocità della luce (vedi appresso) e cioè:

r² - c² t² = r′ ² - c² t′ ² = 0 ;

e poi si prosegue dimenticandosi dell’ = 0 assumendo implicitamente che se un’uguaglianza funzionale vale per un particolare valore delle funzioni deve valere per tutti i valori!

Spetta al Somigliana aver posto la questione del significato fisico delle trasformazioni, anche se tale fatto viene spesso dimenticato.²⁴

2.6) Le ipotesi di Einstein

Il tentativo di dare significato fisico alle trasformazioni di Voigt, effettuato dal Lorentz, col supporre un reale accorciamento delle dimensioni dei corpi fisici in dipendenza della loro velocità, era così incredibile che nessuno volle prenderlo sul serio, quindi le ipotesi fisiche, molto più generali, di Eistein furono considerate come l’unico possibile rimedio alle gravi questioni che poneva la più usuale interpretazione dell’esperimento di Michelson - Morley.

I due postulati su cui si fonda la relatività speciale di Einstein sono:

a) Il postulato della costanza della velocità della luce.

b) Il principio di relatività.

Quest’ultimo può essere illustrato nel modo seguente. All’interno di un sistema inerziale (ovvero, per usare la formulazione originaria di Einstein, un sistema in cui valgano in prima approssimazione le equazioni cli Newton) nessun esperimento può informarci circa la velocità del sistema stesso, rispetto al puramente ipotetico sistema di riferimento in quiete assoluta.

Il postulato a), invece, asserisce che un raggio di luce si muove nello spazio con una velocità costante in modulo, c, indipendentemente dal fatto che il raggio sia emesso da una sorgente in quiete o in moto uniforme rispetto ad un osservatore inerziale (non è chiaro che cosa inerziale ora possa significare, dal momento che il concetto è stato relativizzato; solo nella relatività generale Einstein crede di poter ovviare all’inconveniente).

Einstein assegna a questo postulato un’importanza capitale, anzi, più volte afferma che la teoria della relatività si differenzia dalla teoria di Newton solo a causa del postulato sopra indicato; infatti il postulato b) è valido anche nella fisica di Galileo e Newton.

Con tali ipotesi, Einstein, giustamente dal mio punto di vista, elimina totalmente ogni riferimento all’etere, ente misterioso che occupava, anzi ossessionava, allora le menti dei fisici. E con esso, anche ogni riferimento a moti assoluti, intesi come moti riferiti a un altrettanto ipotetico spazio in quiete assoluta. (Notiamo qui che lo spazio assoluto di Newton non è assoluto perché in “quiete assoluta”, ma lo è, semplicemente, perché non fa riferimento alle “misure sensibili”).

Per Einstein ciò che conta, dal punto di vista della fisica, sarebbe solo il moto relativo come rivelato dalle misure sensibili rispetto a un dato riferimento fisico.

A partire dalle sopraddette ipotesi, il ragionamento di Einstein si può riassumere come segue.

Consideriamo un osservatore O che si consideri in quiete. Esso lanci segnali luminosi ad intervalli di tempo r verso un osservatore O ′, in moto rispetto ad esso, munito di uno specchietto riflettente. Supponiamo di considerare, per semplicità, il moto lungo una retta.

È facile mostrare che se si calcola l’intervallo di tempo di ricezione dei segnali da parte di O ′ (calcolo eseguito da O) si ottiene:

.

L’osservatore O ′ rimandi indietro i segnali ricevuti, tramite riflessione sullo specchietto; ammettendo che in questo processo non si registri alcun ritardo, O riceverà il segnale di ritorno dopo un intervallo di tempo:

.

Qui si è sfruttata l’ipotesi, tutta da verificare, che la velocità del raggio, dopo la riflessione, non dipende dal moto dello specchietto.

Supponiamo ora che il tempo sia universale e che dunque le misure degli intervalli di tempo di O coincidano con quelle di O ′.

Il rapporto tra i tempi di trasmissione di O e quelli di ricezione di O ′ vale:

mentre il rapporto tra i tempi di trasmissione di O ′ (la riflessione si può considerare una trasmissione da O ′ verso O ) e quelli di ricezione di O vale:

Ora, se non si ammette nessuno spazio assoluto privilegiato, il principio di relatività einsteniano richiede che operazioni fisiche simmetriche eseguite da osservatori che si allontanino relativamente l’uno dall’altro diano risultati uguali per R ed R′, ma se il tempo è considerato universale, ciò non potrebbe avvenire, come si vede dalle formule precedenti.

In altri termini, l’ipotesi di indipendenza della velocità della luce dal moto, è incompatibile con una misura dei tempi di ricezione se si assume il tempo assoluto.

Se si cerca la simmetria e si vuole mantenere il postulato di indipendenza bisogna modificare il ritmo di uno dei due orologi, per esempio, quello in moto.

Si può, intanto, imporre l’uguaglianza:

.

Purtroppo i due postulati esplicitamente enunciati da Einstein non sono sufficienti per arrivare alle trasformazioni cercate (vedi la più completa dimostrazione di Notarrigo in questo quaderno); a questo punto Einstein introduce un nuovo postulato (senza la benché minima giustificazione) e precisamente:

(2.6.1) .

Solo con questa ulteriore assunzione si può avere:

che pretendono le trasformazioni di Lorentz.

Il fatto, importante da notare, è che i due postulati di Einstein non sono sufficienti per scrivere il fattore di Lorentz; né, allo scopo, serve la nuova definizione di contemporaneità, come da lui definita (cioè la media aritmetica dei tempi di trasmissione e di ricezione del segnale, come li misurerebbe un osservatore in moto rispetto alla quiete assoluta), che porterebbe a ben altre trasformazioni (vedi l’articolo di Notarrigo), ma bisognerà ammettere la nuova ipotesi, derivante dalla relazione (2.6.1), che corrisponde a una ridefinizione della contemporaneità tale che pretenda la media geometrica tra i due intervalli di tempo sopraddetti, invece, della media aritmetica; ma sarebbe impossibile spiegare il significato fisico di tale operazione matematica, forse bisognerebbe usare orologi logaritmici!

Quindi, questo secondo modo di enunciare l’ipotesi aggiuntiva non trova alcuna giustificazione razionale. Il primo modo equivale a supporre che è indifferente (per ogni fenomeno fisico che utilizzi la luce come mezzo di comunicazione) il fatto che i due osservatori “relativamente” si allontanino o “relativamente” si avvicinino; cosa che, come dice Notarrigo, è assolutamente falsa; a sostegno basta citare l’effetto Doppler che, secondo le stesse deduzioni relativistiche, ci permetterebbe di scoprire il segno della velocità relativa, una volta fissata convenzionalmente l’orientazione relativa dei due sistemi di riferimento. Questo fatto condurrebbe all’assurda conclusione che non sia la stessa cosa l’enunciare il principio di relatività asserendo che i due osservatori vedono le stesse cose se compiono le stesse operazioni, oppure asserendo che non si può rivelare il moto assoluto con operazioni fisiche fatte nello stesso sistema; ciò per la semplice ragione che si sta confondendo un fenomeno “relativo” (come il reciproco allontanamento o avvicinamento) con l’esistenza della quiete “assoluta”, che è quella che si vuole negare.

Fra l’altro, nella fisica dell’effetto Doppler classico (come nel caso delle onde sonore), risulta rilevante financo la condizione che sia l’osservatore piuttosto che la sorgente a muoversi, rispetto all’aria; anche se la differenza è marginale dal punto di vista delle misure effettuabili con i comuni valori ottenibili per le velocità (vedi Perucca).

L’ipotesi che la luce non debba risentire del moto della sorgente è giustificabile solo se si ammette un riferimento assoluto in cui essa viaggi (anche se costante e indipendente dalla sorgente — il riferimento non è detto che sia costituito da un mezzo come il fantomatico etere, ma può anche essere il centro delle cariche elettriche dell’universo) e si assuma una rapida redistribuzione dell’impulso per effetto delle interazioni con il resto dell’universo, come nel caso delle onde acustiche o delle onde prodotte nell’acqua da uno scafo mobile (in questi casi, le interazioni con il resto dell’universo si possono approssimare con gli urti intermolecolari).

Tuttavia, in assenza di un preciso modello fisico che spieghi il significato da attribuire alla parola luce, che Einstein non dà, nonostante asserisca che è la cosa che meglio conosciamo, in assenza di ipotesi fisiche su come avvenga il processo di emissione ed assorbimento di essa da parte della materia, non è affatto banale scartare l’ipotesi che per la luce stessa, in determinate condizioni, si possa ammettere un qualche modo di composizione della sua velocità con quella dell’assorbitore o dell’emettitore (o, nel caso della riflessione, dell’assorbitore - emettitore, infatti dovrà pure interagire la luce con lo specchio per riflettersi!).

L’ipotesi che la luce possa, in certe condizioni, comporsi con il moto della sorgente emittente fu avanzata dal Ritz e ripresa successivamnte dal palermitano La Rosa che la sostenne efficacemente.

L’ipotesi va sotto il nome di “ipotesi balistica”. In base a questa ipotesi la velocità della luce, come osservata da un osservatore, si comporrebbe secondo lo schema “classico”: c + v o c — v, a seconda che la luce venga emessa nel verso del moto o in verso contrario.

L’ipotesi del Ritz fu ritenuta errata dal De Sitter che, secondo il La Rosa, credette di liquidare l’ipotesi balistica senza alcuna giustificazione quantitativa. La giustificazione del De Sitter si basava su una particolare interpretazione dei dati ricavati dalle misure sugli effetti ottici prodotti dal moto delle stelle doppie.

In breve, il De Sitter ragionava così: Se la velocità della luce non fosse costante e indipendente dal moto della sorgente, allora dalla terra non potrebbe nemmeno osservarsi il “fenomeno di stella doppia”, come viene chiamato, perché la luce che ci giunge, inviata in istanti diversi dalle due stelle della coppia, si mescolerebbe lungo il suo cammino impedendoci una ricostruzione razionale degli effetti regolari che invece si osservano e che permettono, invece, una misura della velocità della luce, anche se non troppo precisa.

L’analisi del La Rosa,²⁵ invece, mostrerebbe l’assurdità della pretesa del De Sitter e, anzi, la sua impostazione quantitativa proverebbe che gli osservati fenomeni di intensità variabile, connessi con l’osservazione delle stelle doppie, si spiegano facilmente assumendo l’ipotesi balistica. Non mi risulta che i calcoli del La Rosa, che parte dall’ipotesi del Ritz, abbiano avuto smentite.

C’è, al contrario, una considerazione del Bridgman che, citando il lavoro di La Rosa, lo cosidera come una valida prova di come la luce, in certe situazioni, possa presentare alcuni aspetti tipici di particella.²⁶

Non è il caso, in questa sede, di soffermarci su questa intricata faccenda dell’ipotesi balistica. Ma è sintomatico che, come nel caso del Righi (come vedremo essere accaduto nel caso dell’esperimento di Michelson - Morley), non si citi il lavoro del La Rosa, nemmeno per criticarne i contenuti.

Se si accetta l’ipotesi balistica si può verificare banalmente che nessuna contraddizione può esistere tra il risultato delle misure di ricezione fatte da O e da O ′ nell’esempio prima considerato, nell’ipotesi di un tempo universale, perché si avrebbe sempre R = R ′.

2.7) L’esperimento di Michelson e Morley

L’esperimento di Michelson e Morley (MM) fu congegnato in modo da poter mettere in evidenza il moto della terra rispetto all’etere (supposto esistente) attraverso misure interferometriche.

Descriviamo schematicamente lo strumento essenziale, detto interferometro di Michelson. Immaginiamo di connettere tra loro, rigidamente e “a squadra” (cioè perpendicolarmente tra loro) due aste MA e MB, entrambe di lunghezza l.

Inclinata di 45°, rispetto ad entranbe le aste, si ponga in M una lamina di vetro, L; in modo tale che un fascio di raggi paralleli proveniente da una sorgente di luce, posta in un punto S, venga diviso in due parti (S sta sulla linea che comprende il segmento MB e sta dalla parte opposta a B rispetto ad M).

Una parte del raggio incidente su L si diriga verso A, dopo riflessione in M; l’altra parte del raggio si diriga verso B, dopo rifrazione in M.

Supponiamo che in A e B siano stati posti due specchietti, orientati normalmente alle due aste, che riflettano, di nuovo verso M, i raggi su di essi incidenti.

Qui, il raggio proveniente da A attraversi la lamina L, per rifrazione, e si diriga verso un punto O (O sta sulla linea che comprende il segmento MA e sta dalla parte opposta ad A rispetto ad M), mentre quello proveniente da B, per riflessione, si diriga, anch’esso, verso O. Quindi, a partire dal secondo incontro con la lamina L, i due raggi seguono entrambi lo stesso percorso MO. Supponiamo posto in O un oculare mediante il quale un osservatore possa vedere le frange di interferenza prodotte dalla sovrapposizione dei due raggi.

Si ragionava cosi:

Se lo strumento è in quiete rispetto all’etere (mezzo rispetto al quale si supponeva avvenisse la propagazione delle vibrazioni luminose) i tempi, che i raggi impiegano a percorrere i cammini MAM e MBM, sarebbero uguali.

Al contrario, se lo strumento è in moto rettilineo uniforme rispetto all’etere, p.es., lungo MA, e si suppone che “anche in questo caso” valga la legge di riflessione, secondo la quale l’angolo di incidenza è uguale all’angolo di riflessione, si avrebbe una differenza tra i percorsi dei due raggi, che dovrebbe provocare uno sfasamento nella figura di interferenza.

La sensibilità dell’interferometro di Michelson era tale da permettere di rivelare una velocità (di un moto di traslazione dell’apparato relativamente all’etere) di circa 10 Km/sec.

Se si suppone l’etere fermo rispetto al sole, muovendosi la terra con una velocità di circa 30 Km/sec intorno al sole, risultava possibile rivelare tale velocità mediante lo spostamento delle frange di interferenza previsto.

Risultava più conveniente misurare il rapporto tra le fasi in due direzioni mutuamente ortogonali in quanto tale rapporto risulta essere indipendente, per le ipotesi fatte, dall’effettiva velocità dell’apparato rispetto all’etere, dipendendo solo dall’angolo tra la direzione dell’asta MA e la direzione del moto rispetto all’etere, angolo che doveva variare nel tempo per effetto del moto della terra.

Questo presupponeva delicati aggiustamenti empirici, sia per orientare la lamina L, sia per orientare gli specchi posti in A e B. Operazioni queste, che non erano facilmente controllabili teoricamente.

Non è qui possibile discutere dettagliatamente la teoria dell’etere, in base alla quale venivano fatte le predizioni empiriche. Questo lavoro meriterebbe un riesame critico sia storico che scientifico e ciò andrebbe molto al di là degli scopi che qui ci siamo prefissi. Per cui ne daremo solo un rapido cenno.

Michelson e Morley terminarono i loro esperimenti nel 1887 a Cleveland,²⁷ dando come risultato, entro i limiti di accuratezza del loro apparato sperimentale, l’assenza dello spostamento delle frange di interferenza che ci si aspettava.

Si suole indicare questo risultato come “nullo”.

In base alle loro predizioni teoriche gli autori si aspettavano, invece, un risultato “non nullo”, dal quale si sarebbe potuto ricavare la velocità della terra rispetto all’ipotetico etere.

Dal punto di vista dell’analisi sperimentale, tuttavia, l’esperimento di MM non poteva considerarsi conclusivo. E gli stessi autori mostravano delle perplessità.

Restavano parecchi dubbi.

In che modo la velocità del sistema solare influisce nell’esperimento? Infatti il moto del sistema solare poteva, sottraendosi o aggiungendosi al moto della terra, influire sugli effetti di interferenza.

Qual è l’influenza della temperatura sulle varie parti dell’apparato nei diversi periodi in cui le misure erano state effettuate (p. es., effetto giorno - notte, ecc.)?

In che modo la struttura, solo in prima approssimazione rigida, dell’apparato, può influire sui fenomeni ottici?

In che modo altre condizioni esterne (come, p. es., gli eventi atmosferici) agivano sull’accuratezza delle misure?

I problemi sperimentali erano tali e tanti che altri esperimenti dello stesso tipo furono tentati da altri autori in varie parti del mondo, ma molto tempo dopo il 1887.

Tali altre misure vanno, grosso modo, dal 1920 al 1930, cioè, una trentina d’anni dopo il primo e ben più famoso esperimento. Nell’intervallo si registra un solo esperimento condotto da Morley e Miller tra il 1904 e il 1905.

Un’ampia ed esauriente rassegna di tali esperimenti si può trovare in un articolo dello stesso Miller.²⁸

Tale articolo consente una più chiara idea su quello che ha rappresentato l’esperimento di Michelson e sul suo significato fisico.

I risultati del Miller del 1904 - 1905 indicavano, secondo gli autori, un risultato “non nullo”. Tuttavia, in base alla stessa teoria proposta da Michelson, la valutazione del moto della terra risultava di circa 8 km/sec contro i 30 km/sec che si ricavano dalle misurazioni astronomiche.

Miller ripetè gli esperimenti più volte trovando sempre risultato “non nullo”, salvo qualche rarissima eccezione, oggi, nessuno più parla di tali esperimenti.

Se si fa eccezione per il Miller, che vi dedicò la sua vita,²⁹ in tutti questi delicatissimi esperimenti (circa una decina), si trovarono risultati “nulli”.

Nel 1955 apparve un riesame critico degli esperimenti del Miller, da parte di Shankland e collaboratori.³⁰

In base a questo riesame risulterebbe che anche gli esperimenti del Miller possono considerarsi come “nulli”. La mia impressione, alla lettura di tale articolo, fu che tale riesame era molto più artificioso di quanto non fosse l’analisi originale del Miller.

Il risultato “nullo” fu confermato anche dagli esperimenti più recenti di Kennedy -Thorndike (1932) e di Ives - Stilwell (1938).

Se si accetta il fatto che esperimenti del tipo MM debbano dare sempre risultato “nullo” e si accetta la teoria dell’etere, come allora veniva intesa, si perviene alla supposizione che, lungo la direzione del moto, debba prodursi una contrazione delle lunghezze; tale ipotesi fu suggerita da Fitzgerald e da Lorentz.

In base a tale ipotesi la lunghezza in moto dovrebbe valere 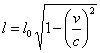, essendo l₀ il valore della lunghezza dell’asta a riposo.

Ma, benché questa ipotesi può essere accettata dal punto di vista della teoria dell’etere, essa non è necessaria. Infatti gli esperimenti “nulli” possono venire coerentemente interpretati anche all’interno della teoria dell’etere come fu mostrato all’epoca.

Diamo un breve cenno su queste interpretazioni che furono avanzate da personalità scientifiche di chiara fama internazionale.

Tra i più autorevoli citiamo Hicks, Sutherland e Righi. Le loro analisi portano a concludere:

a) Le stesse osservazioni sperimentali di Michelson, se interpretate in modo leggermente diverso da come fecero Michelson e Morley, autorizzano la conclusione che il risultato non è “nullo”.

b) Anche ammesso che l’esperimento di Michelson possa essere interpretato come risultato “nullo”, ciò sarebbe ancora in perfetta armonia con le predizioni della teoria ondulatoria dell’etere e del principio di Huygens.

Scrive Hicks:³¹

“Nelle pagine seguenti mi propongo di riconsiderare in dettaglio la teoria generale degli esperimenti con la quale i signori Michelson e Morley cercarono di decidere la questione della quiete o del moto dell’etere, quando un corpo materiale si muova attraverso di esso.

La teoria non è semplice, come potrebbe apparire, essendo essa collegata direttamente all’effettiva riflessione del raggio luminoso su di una superficie in moto.

La correzione dovuta all’alterazione dell’angolo di riflessione è stata introdotta da Lorentz ed è stata tenuta in conto nel lavoro di Michelson e Morley (1887).

Ma la riflessione produce anche un cambiamento nelle lunghezze d’onda dell’onda riflessa…

…Il presente lavoro intende presentare in modo corretto tutte queste correzioni…

Il principale risultato delle correzioni è che nell’esperimento di Michelson e Morley l’effetto da attendersi è esattamente contrario a quello predetto dagli autori …in base a ciò voglio ora mostrare che, invece di un risultato nullo, i dati numerici pubblicati nel loro articolo mostrano una chiara evidenza di un effetto che ci si dovrebbe apettare in base alle analisi che abbiamo condotto”.

Scrive, a sua volta, Sutherland:³²

“L’eperimento di Michelson e Morley, descritto in Phylosophical Magazine (1887), ha posto un dilemma nella fisica dell’etere; a causa del quale la tendenza generale è quella di pensare ad una completa indipendenza dell’etere nelle immediate vicinanze della terra dal moto della stessa.

Si è supposto che questo celebrato esperimento provi definitivamente che la superficie della terra e l’etere adiacente non siano in moto relativo.

Io mi propongo di mostrare come un piccolo cambiamento nel punto di vista della teoria dell’esperimento rende manifesto che, tenendo in conto i particolari aggiustamenti che sono stati fatti all’apparato ottico utilizzato da Michelson e Morley, esso in effetti è stato reso inadatto a decidere sulla questione posta…

In definitiva, se l’osservazione che qui abbiamo fatto è corretta, appare chiaro che il fallimento dell’esperimento di Michelson e Morley è dovuto all’assenza di una particolare precauzione che si rende necessaria per dare allo strumento la sensibilità che da esso si pretende e non mai ad un presunto fallimento della teoria dell’etere”.

Michelson e Morley criticarono le analisi di Hicks.³³ Ma non risulta che siano state opposte obiezioni all’analisi di Sutherland, che a me è sembrata inattaccabile.

Le obiezioni del Sutherland furono riprese dall’italiano Augusto Righi. ³⁴

L’analisi del Righi, tanto profonda quanto sconosciuta, (vedasi, nei già citati articoli, la polemica che il Righi conduce nei confronti di qualche autore che si serve della sua teoria stravolgendone i risultati) mostra chiaramente come una corretta applicazione del principio di Huygens, agli specchi in movimento, dimostra che l’esperienza di Michelson non è in grado di decidere intorno alla questione posta.

Scrive Righi: “Mentre dunque la previsione, formulata da Michelson e fino al dì d’oggi ammessa da tutti, che: si deve osservare uno spostamento di frange passando dal caso in cui la traslazione terrestre si compie parallelemente alla direzione della luce incidente, a quello in cui detta traslazione ha luogo in direzione trasversale, il risultato da me ottenuto è invece questo: che non deve affatto mutare il fenomeno di interferenza passando dall’una all’altra di quelle due orientazioni…

Evidentemente, se questo si fosse saputo prima del 1887 non si sarebbe forse ideata l’esperienza di Michelson, per cui sarebbe probabilmente mancata l’occasione di pensare alla relatività e alla contrazione.”

Si vede dunque come, dal punto di vista dell’interpretazione del risultato relativo all’esperimento di Michelson e Morley, non si avesse unanime consenso. Anzi, molte obiezioni fondamentali, alle quali non fu data un’adeguata risposta, lasciano sospettare che il risultato nullo di Michelson non fosse poi così strano come lo si vuol fare apparire.

Benché oggi, da più parti, si ritiene che la teoria della relatività non si fonda sul risultato di Michelson e Morley, appare paradossale come poi, nel campo della didattica si porti, a conferma del principio di relatività einsteniano, proprio quell’esperimento la cui dubbia interpretazione oggi viene ammessa apertamente dagli specialisti.

In ogni caso, è bene ribadirlo, l’esperimento di Michelson, insieme con la sua interpretazione, riguardava l’ipotesi dell’etere. Questo strano ente, benché di grande utilità pratica nello studio dei molti fenomeni dell’ottica classica, era giustamente considerato all’epoca come un semplice utile modello.

Mediante tale modello si interpretavano facilmente i fenomeni di interferenza, diffrazione e polarizzazione della luce.

Ma era noto che esso non riusciva altrettanto bene, senza l’aggiunta di ipotesi supplementari riguardanti l’interazione dell’etere con i corpi in moto, a spiegare i fenomeni di assorbimento selettivo, ed altri fenomeni più complessi.

Penso che sia necessario dare agli studenti anche una pur minima informazione storica sulla nascita e lo sviluppo delle teorie fisiche e sulle fondamentali questioni filosofiche che esse hanno sollevato, se non si vuole che la scienza appaia come una questione di fede verso le autorità costituite. È semplicemente a tale scopo che ho redatto la presente nota.

Ringrazio i signori collaboratori della Biblioteca Zelantea di Acireale per l’aiuto che mi hanno dato nel consentirmi la consultazione di alcune importanti riviste scientifiche del passato. Desidero anche esprimere la mia gratitudine al caro amico e collega Prof. Notarrigo, che con grande pazienza ha letto attentamente questo scritto. Delle sue positive critiche e dei suoi suggerimenti ho tratto grande vantaggio nella stesura definitiva dell’articolo.

Acireale, 27/2/1991.

NOTE

1. A.Pagano, Fisica e Metafisica nella teoria di Einstein, Mondotre, n. 6/7, anno III, 1989 e Su di un’opera dimenticata di fisica di Boggio e Burali-Forti, Quaderni di Mondotre, Suppl. N. 4/5, anno Il, 1989. TORNA
2. H.Bouasse, La question prealable contre la théorie d’Einstein, Scientia, 1923, p. 13. Bouasse insegnò fisica presso la facoltà si scienze di Toulouse in Francia ed era un fisico sperimentale molto considerato. TORNA
3. G. Peano, Operazioni sulle grandezze, Atti Reale Acc. delle Sc. di Torino, Vol. LVII, 1921-22. TORNA
4. E. Perucca, Fisica Generale e Sperimentale, in due volumi; l’ottava edizione, l’ultima che potè essere curata dall’autore stesso, è del 1963; qualche volta viene citato Einstein in relazione a qualche ipotesi per la spiegazione di qualche fatto sperimentale. TORNA
5. Naturalmente si può procedere anche all’incontrario, dando per nota la somma tra grandezze e definire, mediante questa, la somma tra numeri; come propone Notarrigo nel suo articolo in questo stesso numero dei quaderni. Come sosteneva il Peano, è semanticamente irrilevante la scelta dei termini primitivi in un sistema assiomatico, se tale sistema deve formalizzare un insieme di “verità operative”. TORNA
6. L. D. Landau, E. M. Lifsits, Teoria dei campi, Vol. 2, Edizioni Mir, p. 46, 1976. TORNA
7. Questa idea, che ho già avuto modo di esprimere in altre occasioni (vedi op. cit. a nota 1), verrebbe confermata anche dalle analisi del Christidis. Vedi T. M. Christidis, Annales de la Foundation Louis de Broglie, vol. 14, n. 1, 1989, p. 99. L’autore accosta Einstein ad Eradito, il quale, secondo Diogene Laerzio appartiene alla scuola Ionica, dalla quale scaturisce l’opera di Platone e del suo scolaro Aristotele, e che Diogene contrappone alla scuola Italica, iniziata da Pitagora e che ha prodotto, tra gli altri, anche Democrito. TORNA
8. Vedi: P. W. Bridgman, La logica della fisica moderna, Boringhieri, 1977, p. 163. Bridgman è uno di quei pochi scienziati moderni che pensano e riflettono sui fondamenti del nostro pensiero fisico senza la paura di “sconfinare” negli aspetti filosofici o metafisici della scienza stessa. Del resto, che la relatività nasce da esigenze filosofiche, che potremo definire di stampo empirista, ci è confermato con chiarezza dallo stesso Einstein: (Vedi A. Einstein, Il significato della relatività, Ed. scientifiche Einaudi, 1955, p. 1.): “L’oggetto di ogni scienza, sia delle scienze naturali che della psicologia, è di coordinare le nostre esperienze e dar loro una sistemazione logica …” TORNA
9. L’argomento, che segue nel testo, si trova nel già citato Libro di fisica teorica, (vedi nota 6) a pag. 43 e seguenti. TORNA
10. È invalso l’uso tra i fisici teorici moderni di avvalersi continuamente del “principio di minima azione”. Si ottengono così risultati formali che vengono successivamente rivestiti di significato fisico. La fisica viene così ad essere generata dalla matematica come per miracolo, pressappoco come il coniglio che esce dal cappello del prestigiatore. I più antichi usavano con molta cautela tale procedimento. Già Laplace, che di matematica se ne intendeva, metteva in guardia da abusi del genere: “Molti filosofi colpiti dall’ordine che regna nella natura, e dalla fecondità di mezzi nella riproduzione dei fenomeni, hanno pensato che la natura pervenga sempre al raggiungimento dei suoi obiettivi per vie le più semplici. Applicando questo modo di vedere le cose alla meccanica essi hanno cercato l’economia come strumento di indagine fisica. Tolomeo avrebbe compreso che la luce riflessa va da un punto ad un’altro per il cammino più corto e dunque nel tempo più piccolo possibile supponendo la velocità del raggio luminoso sempre la stessa. Fermat, uno tra i più grandi geni di cui la Francia si onora, ha generalizzato questo principio …” Laplace continua con il notare i contributi di Maupentius e di Newton, e poi aggiunge: “Eulero estende queste supposizioni ai moti variabili istante per istante; e prova, con diversi esempi, che tra tutte le curve che un corpo può descrivere andando da un punto ad un altro dello spazio, esso sceglie sempre quello in cui l’integrale del prodotto della sua massa per la sua velocità e per l’elemento di curva, è un minimo. Così, essendo costante la velocità di un punto materiale che si muove su di una superficie in assenza di forze, esso si sposta da un punto ad un altro per la linea più corta su questa superficie. Si è chiamato l’integrale precedente, “azione di un corpo”; e la riunione di questi integrali simili, relativi ad ogni corpo del sistema, è stata chiamata “azione del sistema”. Eulerò stabili dunque che questa azione è sempre mimima, in modo che l’economia della natura consisterebbe a risparmiare: è in questo che consiste il “principio di minima azione”, del quale bisogna considerare Eulero, come il vero inventore, e che Lagrange in seguito ha derivato dalle leggi primordiali del moto. Questo principio non è in fondo che un risultato curioso di queste leggi, che come abbiamo visto, sono le più naturali e le più semplici che si possa immaginare, e che inoltre sembrano scaturire dall’essenza stessa della materia. Esso si presta bene a descrivere tutte le relazioni matematiche possibili tra forza e velocità, perché basta sostituire in questo principio, in luogo della velocità, la funzione della velocità, per mezzo della quale si vuole esprimere la forza. Il principio di minima azione non deve dunque essere eretto a causa finale; esso è lontano dall’aver dato nascita alle leggi del moto, non ha nemmeno contribuito alla loro scoperta, senza la quale si disputerebbe ancora su cosa bisogna intendere per minima azione nella natura.” TORNA
11. K. T. Bainbridge, Physical Review, Vol. 44 (1933), p. 123. TORNA
12. Le unità di energia cinetica sono date in multipli di e V (elettronVolt), che rappresenta l’energia cinetica che competerebbe ad un elettrone dopo essere stato accelerato da un potenziale elettrostatico di un Volt; 1KeV=1000 eV; 1 MeV=1 milione di eV. TORNA
13. Si indica solo la fonte: Aston, Proc. Roy. Acc., 487 (1927) TORNA
14. Vedasi il manuale di fisica nucleare dell’Evans, The atomic nucleus, McGraw - Hill Company INC (1955), cap. 3. I valori sono dati in termini di difetto di massa, definito come m — A, essendo A il numero di massa del nucleo e m la sua massa. Le unità adottate si riferiscono alla scala dell’ossigeno 16, cioè, 16 uma = massa dell’ossigeno 16; i valori sono dati in unità di 10^-3 uma. Per esempio, per ottenere la massa del protone nell’esperimento di Mattauch (1940) bisognerà porre: m = (1 urna + 8.130 × 10^-3 uma) = 1,008130 uma e così via. TORNA
15. Vedi op. cit. in nota 7 pag.152. TORNA
16. Già il Larmor aveva tentato di ridurre i corpi a singolarità dell’etere : Aether and Matter, Cambridge University Press, 1900. TORNA
17. Vedi A. Einstein, Il significato della relatività, Ed. Einaudi, p. 37, 1955. TORNA
18. Per maggiori dettagli sulla questione e per una derivazione “covariante” si veda S. R. De Groot, The Maxwell Equations, North - Holland, 1969. TORNA
19. Al posto dei vettori E e B, Lorentz usava i vettori D e H, molti altri autori usano i vettori E e H. Nel vuoto non c’è sostanziale differenza tra le varie scelte; la differenza è fondamentale nei mezzi ponderabili. Ma la confusione simbolica sta ad indicare la confusione sui significati fisici che sempre si è avuta in materia, vedi a p. 12 - 13 del riferimento citato nella precedente nota. TORNA
20. Come fa il Dugas (vedi R. Dugas, Histoire de la Mécanique, Éd. du Griffon, 1950), lo stesso Lorentz in una nota del suo fondamentale lavoro sulla dinamica dell’elettrone, del 1905, conferma tale paternità. TORNA
21. Voigt stabilisce molte delle proprietà a cui obbedisce l’equazione d’onda classica nel lavoro Ueber das Doppler’sche Prmcip, Nachrichen der K. Gesder Wiss. zur Gottingen, 10 Mar 1887. TORNA
22. Vedi l’articolo di Notarrigo in questo quaderno. TORNA
23. Come esempi si vedano il Landau (già citato); R. B. Leighton, Principles of Modern Physics, McGraw - Hill, 1959; ecc., ecc. TORNA
24. Vedi M. C. Somigliana, Rendiconti R. Acc. dei Lincei, Vol. 31, 1922 TORNA
25. Si veda: M. La Rosa, Le concept de temps dans la theorie d’Einstein, Scientia, Vol. XXXIV (1923). TORNA
26. P.W. Bridgman, op. cit., nota 7 a p. 163. TORNA
27. A. A. Michelson and E. Morley, Am. J. Sci., 34, 333 (1887). TORNA
28. D. C. Miller, The Ether drift experiment and the determination of the absolute motion of the earth, Rev. Modern Physics, vol. 5,1933. TORNA
29. Sembra che il Miller godesse di alta considerazione come autorevole ed espertissimo sperimentatore, tant’è vero che lo stesso Einstein, più volte, lo sollecitò a proseguire nei suoi esperimenti. TORNA
30. R. S. Shankland et al., Rev. Modern Phy., Vol. 27, n.2 (1955), p. 167. TORNA
31. W. M. Hicks, On the Michelson - Morley Experiment and the Drift of the Ether, Phil. Magazine, Vol. 3, p. 9 (1902). TORNA
32. W. Sutherland, Relative Motion of Earth and Ether, Phy. Mag., Vol. 45, p. 23 (1898). TORNA
33. In Phy. Mag., T. IX, p .680. TORNA
34. Vedi la I e la II memoria della R. Acc. Dell’Ist. di Bologna, Tomo 6, 57. (1916), ripublicate nel Nuovo Cimento, rispettivamente negli anni 1919 e 1921. TORNA