REALE O FORMALE?

Salvatore Notarrigo

Il mio amico Boscarino mi ha chiesto di contribuire con un mio articolo sull’argomento che dà il titolo a questo numero dei Quaderni di Mondotre, dal punto di vista di un fisico.

Ho avuto qualche remora per le seguenti considerazioni:

1) Ho già letto l’articolo di Boscarino qui pubblicato e gli estratti di Peano assieme pubblicati e non mi sembra che ci sia nulla da aggiungere da qualsiasi punto di vista.

2) Ho già pubblicato su questi Quaderni¹ qualcosa sull’argomento per parlare della concezione della scienza degli antichi filosofi Italici e non mi piace scrivere sempre le stesse cose.

3) Interamente d’accordo con la filosofia di tali antichi filosofi, per me la scienza è una e indivisibile e deriva semplicemente dall’accordo tra le regole del nostro linguaggio e la nostra esperienza. Mi riesce difficile distinguere il concetto che io ho della fisica dal concetto che io ho della matematica, o quest’ultimo da quello che io ho della logica, o il mio concetto di algebra dal mio concetto di grammatica.

In un mio intervento ad un covegno su Archimede notavo che nei discorsi dei fisici, Archirnede risultava un fisico, in quelli dei matematici, risultava un matematico, e così via. Negli atti del convegno² scrivevo:

“Spesso gli elogiatori di Archimede gli rendono un ben misero servizio riducendolo chi a ‘sommo matematico’, chi a ‘grande ingegnere’, chi a ‘padre della fisica matematica’.

Credo che Archimede avrebbe rifiutato cotali appellativi che non avrebbe nemmeno compreso, perché per lui ‘filosofia’, ‘matematica’, ‘fisica’, ‘ingegneria’ erano tutti sinonimi, come nella tradizione di tutti i cosiddetti presocratici e sarebbe sicuramente andato fuori dai gangheri nel sentirsi assimilare, per qualche verso, a Platone o ad Aristotele, le cui dottrine erano la negazione stessa della sua filosofia.”

Tuttavia la storia del pensiero ci insegna che con il linguaggio si può parlare coerentemente anche del sesso degli angeli e non ci sono scienze in cui sia facile distinguere il reale dal formale o il formale dall’ideale.

Basta per questo consultare un qualsiasi dizionario filosofico per accorgersi che nella storia della filosofia quelli che in una certa epoca venivano classificati come “idealisti” in un’epoca successiva venivano ad essere qualificati come “realisti” e viceversa.

Lo stesso è successo sui discorsi sulla filosofia della matematica a proposito dell’alternativa “formalisti - costruttivisti” ecc.

Potrebbe sembrare una questione puramente nominalistica, riferentesi solo alla definizione dei termini. Ma si scopre che è una questione molto più profonda che ha a che fare con la concezione del mondo, con la metafisica e, in particolare, con l’ontologia dei vari filosofi o di una particolare epoca o di una categoria sociologica di persone.

Così ho deciso di rimaneggiare in qualche modo gli appunti che avevo preparato come preambolo per gli studenti del mio corso di Fisica Superiore.

***

Nel leggere un qualsiasi testo di fisica noi incontriamo delle proposizioni espresse con l’uso del linguaggio comune e delle proposizioni espresse nella forma simbolica del linguaggio matematico.

Spesso i simboli possono essere tradotti con dei termini che, se pur espressi con vocaboli della lingua comune, assumono dei significati molto particolari che non vengono generalmente indicati nei comuni dizionari della lingua corrente.

Per comprendere il significato preciso di alcuni termini della fisica spesso occorre leggere e comprendere diversi libri di fisica. Anzi, sul significato di alcuni termini, spesso, non si riesce a trovare un accordo nemmeno tra gli stessi specialisti del particolare ramo a cui il termine stesso si riferisce.

Alcune volte i simboli che compaiono nelle formule della fisica non hanno un significato reale univocamente definito, perché semplicemente stanno al posto di un qualsiasi individuo che obbedisca a determinate relazioni formali, che interamente lo definiscono. E queste restano sempre vere indipendentemente dal preciso significato reale del simbolo.

Un antico ideale di molti scienziati è sempre stato quello di poter costruire un linguaggio scientifico tale che ogni termine o proposizione potesse avere un unico significato, sempre definito in modo non ambiguo, sia che si tratti di un “significato reale” che di un “significato formale”.

Un tale linguaggio secondo Leibniz dovrebbe avere la forma di

“un calcolo nuovo e mirabile, col quale sia possibile esprimere ogni nostro ragionamento e che possa procedere come quello dell’aritmetica e dell’algebra. Con tale calcolo si potrebbe sempre chiudere ogni controversia, a partire dai dati iniziali. Di modo che, prendendo in mano una penna e bandendo ogni verbalismo, i due disputanti possano dirsi l’un l’altro: calcoliamo, allo stesso modo di come due aritmetici decidono di un errore di calcolo.”

In tale spirito chiediamoci qual è il significato di “significato reale” e di “significato formale”, concetti che abbiamo sopra menzionato.

Ci accorgiamo subito che, intanto, dovremmo conoscere preventivamente il significato di ‘significato’. Tuttavia per saperlo occorrerebbe conoscere il significato del ‘significato’ di “significato”!

Constatiamo banalmente che, continuando per questa via, otterremmo semplicemente un regresso all’infinito e non potremmo mai venirne a capo. Infatti interi libri sono stati dedicati a tale problema, senza alcun sensibile risultato.

Per risolvere un problema logicamente irresolubile, come in particolare è il precedente, siamo costretti a fare, in qualche punto, un’asserzione di ordine metafisico, cioè non verificabile empiricamente, nè dimostrabile logicamente e che tuttavia abbia un significato il quale, comunque, sia in grado di interrompere la catena infinita.

Ma, per il semplice fatto che tale asserzione deve necessariamente essere di ordine metafisico, risulta chiaro che ognuno potrà ritenersi libero di fare una sua particolare scelta. Si può dire, infatti, che tutta la storia del pensiero è contrassegnata dalle varie risposte che sono state date al nostro problema.

Dovremmo perciò concludere che il sogno di Leibniz è veramente un ‘‘sogno’’?

In ogni caso, però, abbiamo capito una cosa molto importante: per sapere il significato di un qualunque termine dobbiamo necessariamente uscire fuori dai puri giochi di parole e appellarci alla realtà. Ma che cos’è la “realtà”?

Anche qui i filosofi e gli scienziati, in tutte le epoche della storia del pensiero, si sono sbizzarriti a darne le più svariate definizioni.

Tuttavia dal passato ci è pervenuto un modello mirabile di linguaggio scientifico, al quale tutti i grandi scienziati del passato si sono sempre ispirati, e che certamente ha prodotto il sogno leibniziano. Esso è rappresentato dagli “Elementi” di Euclide.

In tale libro si trova raccolta, in forma lucida e coerente, la maggior parte di quelle conquiste del pensiero che in gran parte erano già state ottenute nei secoli precedenti all’interno della tradizione pitagorica. Il risveglio della scienza, dopo la lunga parentesi medievale, si deve proprio alla riscoperta del testo di Euclide e dei testi di Archimede, che è stato il suo più grande continuatore.

Sia Euclide che Archimede non ci hanno dato risposte teoretiche ai problemi che prima abbiamo posto, in quanto sembra che essi si siano limitati solo a dare degli “assiomi” e a dedurre dei “teoremi” in determinate situazioni particolari.

Quindi, se vogliamo sapere quale risposta essi abbiano potuto dare ai pregiudiziali problemi che abbiamo prima posto, non ci resta che esaminare le operazioni che concretamente essi hanno compiuto.

Intanto osserviamo che essi usavano la lingua comune dei loro tempi ma si nota, in modo inequivocabile, che essi la usavano in un senso molto più preciso e molto più “formale” di quanto non facessero i filosofi, gli storici, ecc., del loro tempo.

Qui, ancora una volta, ci siamo imbattuti di nuovo nell’aggettivo “formale” ed è bene darne ora il suo significato. Ma, non potendone dare una “definizione nominale”, ci limiteremo a darne una “descrizione”.

Col termine “descrizione”, spesso detta anche “definizione reale” intendererno un insieme di parole, corredate da specifici esempi concreti, le quali abbiano un significato comunemente accettato, il più possibile privo di ambiguità. Come esempio diamo qui di seguito la “descrizione” del termine “definizione nominale”.

“Col termine “definizione nominale” intenderemo una proposizione in cui compaia il segno =, dove a sinistra di = compaia un termine, del quale se ne vuole conoscere il significato, e, a destra di = compaiano una serie di termini, di cui se ne suppone noto il significato”.

Esempio:

pentagono = poligono con cinque lati.

Con la precedente “descrizione” abbiamo dato il significato di = e anche quello di “definizione nominale”, cioè: una “definizione nominale” ha la “forma”

(1) a=b ,

dove a, in modo generico, indica un qualunque termine che si vuole definire; b, in modo generico, indica il complesso di termini di significato noto che definiscono il generico termine a, ed il segno = è stato messo al posto del termine “significa”, cioè “a e b sono nomi diversi dello stesso oggetto”, ovvero, equivalentemente, “a e b hanno lo stesso significato”.

A questo punto non è più necessario sapere il significato di significato. Il significato di una parola è quell’oggetto della nostra mente, cioè quell’“idea”, che intendiamo evocare esprimendo quella parola.

All’“idea” noi possiamo associare degli oggetti che noi pensiamo come esistenti concretamente nello spazio e nel tempo o, anche, oggetti astrattamente esistenti solo nella nostra mente.

Con la (1) abbiamo dato un particolare esempio di una relazione “formale”, dove compaiono due lettere a e b di significato indeterminato, comunemente ma impropriamente chiamate “variabili” ma dove anche compare il segno al quale, invece, abbiamo dato un ben preciso significato “reale” (per tale ragione spesso esso si dice una “costante” e, nel caso particolare, una “costante logica”) che esprime la relazione di “identità logica”.

Anche noi, nel seguito, useremo il termine “variabile”, anche se esso e improprio per il fatto che non esprime alcuna variabilità ma la semplice convenzione che ai simboli a e b possiamo sempre sostituire due termini qualunque, purché dotati di un unico significato. Essi servono solo per individuare le relazioni “formali” esistenti fra generici termini, che, pur avendo significati individuali diversi, condividono le stesse relazioni formali.

Facciamo ora altri esempi di relazioni puramente “formali”, ma in un campo diverso da quello della “logica”. Li prenderemo dal campo della “grammatica” .³

Consideriamo le due proposizioni seguenti:

(a) “l’uomo è animale razionale”,

(b) “uomo consta di quattro lettere”,

esse esprimono, rispettivamente, una proprietà reale ed una proprietà formale di uomo.

L’una si riferisce all’ente, o se si vuole all’idea che noi abbiamo di esso, l’altra alla parola, che semplicemente lo denomina.

Anche la proposizione

(c) “uomo è sostantivo”

esprime una proprietà formale.

Un criterio per decidere sulla questione se la proprietà sia reale o formale è quello di sostituire alla data parola una parola equivalente, anche di altra lingua. Se al posto di uomo metto l’equivalente inglese man, la (a) resta vera, mentre la (b) risulta falsa. Concludiamo che la prima è una proprietà reale e la seconda è formale.

Tuttavia, con un tale criterio, la (c) non può essere decisa, ciò per il fatto che nelle lingue europee si ha la stessa classificazione grammaticale del latino.

Ma è noto che vi sono lingue che non distinguono le varie forme grammaticali (cioè: sostantivo, aggettivo, verbo, ecc.).

Ma anche in latino e nelle altre lingue neolatine vi sono diversi esempi in cui la distinzione, in quanto puramente formale, si perde. P. es.:

Homo homini lupus. (“lupus” usualmente qualificato come sostantivo assume qui la funzione grammaticale di verbo).

Ars longa, vita brevis (gli aggettivi “longa” e “brevis” diventano verbi).

Pietro è buono, Pietro è poeta (l’aggettivo “buono” ed il sostantivo “poeta” funzionano entrambi da aggettivi).

Si potrebbe costruire una lingua, ed il Peano ne ha dato un esempio, in cui possono venire completamente eliminate le forme grammaticali e che va nella direzione del sogno leibniziano.

Anche i simboli della matematica costituiscono un esempio di lingua senza grammatica: la proposizione 2 + 3 = 5 si potrebbe tradurre in lingua italiana con “la somma dei numeri due e tre fa il numero cinque”. Le parole della traduzione hanno ora una grammatica, la quale tuttavia non aggiunge niente alla più chiara e più breve forma simbolica.

Anche in matematica si hanno proprietà reali e proprietà formali:

“ è frazione minore di 1”

“è frazione irriducibile”.

Ponendo nella prima al posto di la proposizione resta vera. Facendo la stessa sostituzione nella seconda, essa diventa falsa. Quindi, la prima esprime una proprietà reale e la seconda una proprietà formale.

I precedenti esempi sono sufficienti per comprendere il significato dei termini “reale” e “formale”, e i diversi sensi contestuali di “formale”. Nel seguito, quando useremo il termine “formale”, lo intenderemo sempre in senso “logico” e non “grammaticale”, ma è necessario avvertire che nella maggior parte dei libri di logica moderni, pur usandosi i simboli introdotti dal Peano, non si distingue più tra logico e grammaticale, tornando a fare riferimento alla logica grammaticale di Aristotele, che il Peano intendeva superare.

Nella lingua comune noi usiamo spesso delle proposizioni della forma:

“Socrate è filosofo”

“Due è numero”.

Con esse vogliamo dire che gli “individui” Socrate e due appartengono, rispettivamente, alle “classi” filosofo e numero.

Secondo la forma grammaticale ‘Socrate’ e ‘due’, sono “soggetti”, ‘è’ è “copula”, ‘filosofo’ e ‘numero’ sono “predicati”.

Tale classificazione grammaticale vale anche per le seguenti proposizioni:

“Etna è Mongibello”

“mais è granturco”

“numero pari è multiplo di due”.

Ma, dal punto di vista della logica, esse non esprimono la relazione tra un individuo e una classe ma, piuttosto, la relazione di identità logica tra soggetto e predicato, quindi in questo caso dovremmo scrivere

“Etna = Mongibello”

“mais = granturco”

“numero pari = multiplo di due”.

Ne viene che la forma grammaticale non solo non ci dice niente sulle relazioni logiche ma addirittura le confonde. In un linguaggio scientifico bisogna eliminare tali ambiguità e, allora, al posto dell’unico termine ‘è’ ne dobbiamo introdurre più di uno per poter esprimere, in modo non ambiguo, le diverse “relazioni logiche”.

Peano ha introdotto il simbolo Î per indicare la relazione logica tra individuo e classe, ed il simbolo = per indicare l’identità logica.⁴

Nella lingua comune il significato della copula non si limita a questi due che abbiamo sopra menzionato. Infatti nella proposizione:

“filosofo è uomo”,

si vuole dire che la “classe” ‘filosofo’ è una parte della “classe” ‘uomo’.

Peano introduce il simbolo É per quest’altra relazione.⁵

E, ancora:

“qualcuno è filosofo”.

Qui si vuole dire che esistono individui che appartengono alla classe “filosofo”, o, come spesso anche si dice, la classe “filosofo” non è vuota.

Per quest’altro significato della copula nessuna delle tre relazioni precedentemente introdotte si adatta. Useremo il simbolo di Peano $, e la precedente relazione si scriverà nel caso specifico

$ filosofo ,

o genericamente

$a ,

dove a è una classe.⁶

Vediamo alcune altre ambiguità della lingua comune che è necessario togliere in un linguaggio scientifico.

Generalmente in italiano, si usa la congiunzione ‘e’ per dire che per un determinato individuo si pretende che abbia nello stesso tempo due proprietà, come nella proposizione “In Italia i soldati sono di sesso maschile e di età superiore ai 21 anni”. Se tale proposizione è vera ne segue che se qualcuno ha 15 anni o è di sesso femminile non può essere un soldato.

Ma Supponiamo che salendo su di un autobus incontriamo la scritta “Riduzione per militari e per minori di anni 6”, noi sicuramente interpreteremmo la ‘e’ nel significato usuale della disgiunzione ‘o’, dal momento che è impossibile trovare un minore di anni 6 che sia anche un soldato. Al posto della congiunzione ‘e’, nel primo dei due significati, Peano usa il simbolo ∩, e, per il secondo significato, cioè nel più comune significato di ‘o’, usa il simbolo U. Ma ancora si hanno delle ambiguità nell’uso della disgiunzione ‘o’. P.es., nella proposizione “è necessario che venga uno studente o un professore”, non è affatto chiaro se basti che venga uno qualsiasi dei due o, eventualmente anche tutti e due, oppure se sia da pensare che con la precedente affermazione si pretenda invece che la venuta dell’uno debba escludere categoricamente la venuta dell’altro. Il primo significato si suole dire “disgiunzione inclusiva” ed il secondo, “disgiunzione esclusiva”.

Nel seguito converremo che il segno U debba intendersi solo nel primo significato; non sarà necessario introdurre un segno speciale per il secondo significato, perché, come vedremo, lo si potrà esprimere mediante la combinazione di altri segni.

Un’altra comunissima ambiguità della lingua italiana ha a che fare con la negazione; infatti, alle due proposizioni, “non e venuto nessuno studente” e “non è venuto alcuno studente”, si suole dare lo stesso significato, tuttavia si dice che “nessuno = non alcuno” e anche si dice che due negazioni affermano! Peraltro, in molte frasi il “non” ha solo valore pleonastico, per cui la sua presenza o assenza non altera per niente il significato della frase.

Nel seguito per la negazione useremo il segno ~ .

Finora abbiamo introdotto sette segni speciali per altrettante costanti logiche:

=, Î, É, $, ∩, U, ~ .

Tuttavia tutte queste costanti non sono “logicamente indipendenti”, nel senso che alcune di esse possono essere legate alle altre per mezzo di opportune definizioni nominali. In altre parole, possiamo, se vogliamo o se lo riteniamo utile, sceglierne solo alcune per fungere da “termini primitivi” e considerare le altre come “termini derivati”, cioè definiti a partire dai termini primitivi, mediante appropriate asserzioni della forma (1).

Risulta irrilevante la scelta dei termini che si vogliano assumere come primitivi, scelta che dipende dagli scopi. Spesso si sceglie la via di minimizzare il numero dei termini primitivi, ma anche questo si può fare in più modi.

Facciamo alcuni esempi:

Supponiamo di introdurre la definizione

(2)

Per il momento converremo che il segno ∩ debba stare sempre tra due classi e che il risultato dell’operazione sia ancora una classe e converremo, anche, che il segno ~ si applichi sempre ad una classe e produca la classe complementare.

Quindi, la (2) significa che dobbiamo prima trovare l’“intersezione” delle classi a e b e dopo trovarne il “complemento”.

Possiamo compiere delle “operazioni fisiche elementari”, con carta e penna, che modellizzino le precedenti operazioni logiche. Tali modelli si sogliono chiamare “diagrammi di Venn”. Tali diagrammi consistono nel disegnare, nel piano, opportune figure geometriche chiuse, p. es., cerchi e intersezioni tra cerchi.

Con tali figure possiamo rappresentare le varie classi. Ogni punto entro il perimetro di una delle figure rappresenta un individuo della corrispondente classe. P. es.. la classe a∩b è rappresentata dall’area in grigio nel seguente diagramma.

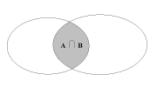
La classe sarà rappresentata da tutto il resto del piano, quando ne venga esclusa la porzione in grigio.

Assumendo l’operatore “^~” (detto spesso “operatore di Sheffer”) come termine primitivo si possono definire nominalmente, come si verifica facilmente aiutandosi con i rispettivi diagrammi di Venn, le costanti logiche ~, ∩, U con le seguenti definizioni nominali:

(3) .

Con la (3) si definisce il “complemento” di una classe; per brevità possiamo porre:

(4) .

Asseriamo come assioma la:

(5) .

Successivamente possiamo definire nominalmente l’“unione” tra due classi con la:

(6) ,

e, ancora, l’“intersezione” tra due classi con la:

(7) .

Questo risultato ci invita a sottintendere il segno ∩ con la seguente definizione nominale:

(8) .

Con le precedenti definizioni abbiamo eliminato tre simboli mediante l’introduzione di un unico simbolo che funge da termine primitivo. Tuttavia è utile mantenere tutti e quattro i simboli, per rendere più brevi e più perspicue le formule, fermo restando che, quando si vuole, è sempre possibile sostituire, usando le definizioni nominali precedenti, tutti i termini derivati con l’unico termine primitivo ^~, come già abbiamo fatto nella (7).

Possiamo anche eliminare dal novero dei termini primitivi la costante logica É ponendo per definizione:

(9) (a É b) = (ab = a).

Notiamo che l’operatore ^~ (e conseguentemente anche ~, ∩, U) opera su due classi e produce una classe. Mentre la relazione É opera tra due classi e produce una proposizione, tuttavia anche la (9) è verificabile con operazioni fisiche elementari costruendo l’opportuno diagramma di Venn.

Finora abbiamo incontrato quattro tipi di proposizioni:

(10) x Î a ,

(11) x = y ,

(12) a É b ,

(13) $a ,

la (10) lega un individuo ad una classe; la (11) lega tra loro due termini ed è irrilevante che essi siano individui, classi, proposizioni, o qualsiasi altro oggetto, anche al di fuori dei termini propri della logica, purchè abbiano un significato; la (12) lega tra loro due classi; la (13) afferma una particolare proprietà di una determinata classe.

Tuttavia notiamo che i termini della logica: “individuo”, “classe”, “proposizione”, hanno significato puramente “formale” e nessun significato “reale”. P. es.:

Socrate Î filosofo,

filosofo Î classe,

(Socrate Î filosofo) Î proposizione.

Nella prima “filosofo” compare come classe, nella seconda come individuo, nella terza: la proposizione “Socrate Î filosofo” compare come individuo e “proposizione” compare come classe.

Da questi esempi viene l’idea di abolire i termini “individuo, classe, proposizione”, con l’adottare la convenzione che i termini che figurano a sinistra di Î si debbano sempre intendere come “individui”, i termini che figurano alla sua destra si debbano intendere come “classi” e gli oggetti della forma “x Î a” siano le “proposizioni elementari”. Tuttavia per far questo dobbiamo prima poter ridurre le proposizioni (11), (12), (13) alla forma elementare (10).

Allo scopo conviene introdurre alcune altre costanti logiche.

Introduciamo l’operatore ι che, operando su di un termine qualsiasi y, lo trasformi in una classe a= ιy, tale che “solo” per l’oggetto al quale abbiamo dato il nome y abbia senso scrivere y Î a.

Avremo:

(14) (y Î ιy) = (y = y)

ovvero

(15) (Î ι) = (=) .

Possiamo leggere ι come “identico” e ιy come la “la classe degli identici all’individuo y” o anche, “il nome dell’individuo y” o “l’idea di y”.

Una classe con un solo individuo della forma a = ιx la chiameremo un “elemento” (viene chiamata anche “idea”, “atomo”, “singleton”).

Possiamo, se vogliamo, eliminare formalmente il segno =, mediante la (15), dal novero dei termini primitivi, introducendo ι come termine primitivo, scrivendo:

(16) (=)Î ι (Î ι) .

Ma, qualunque scelta vogliamo fare, anche la (11) si potrà sempre scrivere nella forma (10) con la:

(17) (x = y) = (x Î ιy) .

Allo stesso modo possiamo introdurre l’operatore á , il quale operando su di una classe b produce un’altra classe áb , i cui individui sono tutte le parti di b, cioè le sottoclassi a di b e per le quali, perciò, si ha sempre a É b.

Potremo scrivere:

(18) (a É b) = (a Î áb) ,

cioe: a è parte di b = a Î (parte di b).

Ovvero:

(19) ( É ) = ( Î á ) .

E, quindi, anche la (12) si può scrivere nella forma (10).

Per scrivere anche la (13) nella forma (10), si può introdurre una nuova costante logica che “formalmente” si comporti come una classe e che però e definita da una proprietà “assurda”, cioè autocontraddittoria, cioè tale che di nessun individuo si possa asserire che abbia una tale proprietà, o classe che dir si voglia, che possiamo chiamare il “nulla”, potremmo indicarla con la lettera A, abbreviazione di Assurdo, ma conviene risparmiare le lettere dell’alfabeto, da impiegare per le variabili o per le costanti extralogiche, introducendo in sua vece il simbolo Ù.

Allora possiamo scrivere:

(20) ($a) = ~ (a = Ù) .

Nella (20) il segno ~ nega tutta la proposizione a secondo membro della prima identità, ma si può convenire di porlo a negare la relazione che vi compare con significato identico:

(21) (a ~ = Ù) = ~ (a = Ù) ;

per la (15) possiamo anche scrivere:

(22) (a ~ = Ù) = (a ~Î ιÙ) .

È ovvio che i segni ~ e Î godono della proprietà commutativa:

(23) (~Î) = (Î~) ,

e quindi

(24) (a ~Î ιÙ) = (a Î~ ιÙ) ,

che per la (4) si può scrivere:

(25) (a Î~ ιÙ) = (a Î ) .

Infine, per le identità da (20) a (25), anche la (13) si può scrivere nella forma (10) con la:

(26) ($a) = (a Î )

E così, se abbreviamo con I il termine “individuo”, con C il termine “classe”, con P il termine “proposizione”, consentendo che i segni É e ∩ possano operare anche tra proposizioni, col rispettivo significato di “implica” e della congiunzione “e” possiamo allora porre la convenzione:

(27) ((x Î a) Î P) É ((x Î I) ∩ (a Î C )) ,

che possiamo leggere

“se la scrittura ‘x Î a’ é una proposizione allora ‘x’ é un individuo ed ‘a’ è una classe.”

La (27) ci permette di non nominare più i termini I, C, P, perchè la forma x Î a ci dice tutto sulla natura formale dei termini che vi compaiono.

Allo stesso modo possiamo porre:

(28)

che ci permette di formare classi a partire da altre classi, senza bisogno di asserire esplicitamente che un dato simbolo rappresenti una classe.

Per la convenzione (27), in base alla (17), possiamo asserire che qualunque cosa sia y, ιy è una classe:

(29) ιy Î C ;

e, in base alla (18), anche:

(30) ( a Î C ) É ( áa Î C ) .

Dalla (10) si vede che il simbolo “x Δ si può considerare come un operatore, con parametro x, che indichiamo con Î_x , che ad ogni classe a fa corrispondere la proposizione elementare a_x = x Î a. Possiamo scrivere quindi:

(31) Î_x = x Î ,

(32) a_x = Î_x a = x Î a .

Si può definire l’operatore inverso '_x , che ad ogni proposizione riguardante x faccia corrispondere la classe relativa, con la definizione nominale:

(33) '_x a_x = a .

Ovviamente si ha:

(34) Î_x '_x a_x = a_x ,

(35) '_x Î_x a = a .

Allo stesso modo, se

a = ι x

si può definire l’operatore inverso di ι con la:

(36) לּ a = לּ ι x = x

Si ha, ovviamente,

(37) ι לּ a = ι לּ ι x = ι x = a .

L’operatore '_x , si può interpretare come il segno per la formazione di classi e la (33) si può leggere “la classe degli individui x per cui vale la proposizione a_x”.

L’operatore ι fa passare da un individuo al suo elemento, l’operatore inverso לּ fa passare da un elemento al suo individuo. Notiamo che il dominio dell’operatore לּ è limitato agli elementi, cioè a classi con un solo individuo, mentre il dominio di ι non ha limitazioni, essendo che qualunque cosa può fungere da individuo di una determinata proposizione.

Le costanti ~, ∩, U, ̃ si possono usare anche tra proposizioni con il significato, rispettivamente, di “negazione, congiunzione, disgiunzione inclusiva, esclusione della congiunzione” e, analogamente alle relazioni da (2) a (9), si possono scrivere le:

(38) .

(39) .

(40) .

(41) .

(42) .

(43) .

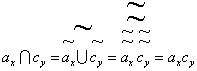(44) .

(45) (a_x É b_y) = (a_xb_y = a_x) .

Analogamente alla (28) si può convenire che:

(46) ,

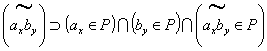la quale permette di formare “proposizioni composte” a partire da “proposizioni elementari” o da altre “proposizioni composte”.

Se si vuole si può eliminare anche il segno Ù dai termini primitivi, per cui i termini primitivi della logica si possono ridurre solamente a tre (p. es. =, Î, ̃, ma, ovviamente, è possibile scegliere, opportunamente, una terna diversa). Per far questo basta porre:

(47) .

La sua classe complementare sarà:

(48) .

che è la classe “banale”, della quale ogni cosa pensabile si può considerare un suo individuo; essa si può chiamare anche il “tutto” o l’“essere”. Per cui le affermazioni x Î Ù e x Î Ú si possono semplicemente leggere “x non è” e “x è”, rispettivamente.

Diceva Parmenide:

“Bisogna che il dire e il pensare sia l’essere: è dato infatti essere, mentre nulla non è”.

Senza pericolo di ambiguità, possiamo usare i due simboli precedenti anche per le proposizioni, ponendo:

(49) Ù = $Ù ,

(50) ,

che possiamo chiamare, rispettivamente, la “contraddizione” e la “tautologia”, quando riferite a proposizioni.

Quindi se p è una qualunque proposizione, “p = Ù” si potrà leggere “p è una contraddizione” o “p è assurda” o “p è necessariamente falsa”, ecc. e l’asserzione “p = Ú” si potrà leggere “p è una tautologia” o “p è banale” o “p è necessariamente vera”.

Se a è una classe, le seguenti asserzioni:

(51) $ a = ( a ¹ Ù) ,

(52) ,

(53) ,

(54) ,

si possono leggere rispettivamente:

è possibile che vi siano degli individui che hanno la proprietà a,

è possibile che vi siano degli individui che non hanno la proprietà a,

è necessario che non vi siano individui che abbiano la proprietà a,

è necessario che ogni individuo abbia la proprietà a.

È noto che i logici medievali attribuivano tali affermazioni ad una particolare estensione della logica che chiamavano “logica modale”, ma come si vede non è per niente necessario instaurare alcuna logica speciale, anche se oggi vi sono i moderni continuatori della logica scolastica.⁷

***

Così come alcuni termini (cioè i “termini derivati”) si possono definire a partire dai “termini primitivi”, allo stesso modo, alcune proposizioni (cioè i “teoremi”) si possono asserire a partire dalle “proposizioni primitive”, le quali ultime vengono divise in “assiomi” e “definizioni”.

Anche in questo caso è spesso possibile scambiare il ruolo di assiomi, definizioni e teoremi, la scelta è irrilevante purché si arrivi, alla fine, alle stesse proposizioni, mediante l’uso di appropriate “regole deduttive”. Quindi anche questi termini hanno solo valore “formale”. Un insieme di “assiomi, definizioni, teoremi e regole deduttive” si dice un “sistema deduttivo”. Due sistemi deduttivi che abbiano lo stesso insieme di proposizioni asserite, anche se con diversa scelta degli assiomi e delle definizioni, si dicono “equipollenti”.

Per il sistema deduttivo della “logica”, le regole deduttive possono essere molto semplici. Noi useremo le tre seguenti:

I) In ogni proposizione asserita si può sostituire qualsiasi simbolo che rappresenti una “variabile” con un qualsiasi altro simbolo di variabile, con la “condizione” che la stessa sostituzione debba effettuarsi in tutti gli altri posti in cui la detta “variabile” compaia col medesimo significato reale.

II) In ogni proposizione asserita se ‘a’ è un simbolo o un qualsiasi gruppo di simboli, esso si può sostituire (anche senza la “condizione” posta in I) con un qualsiasi altro simbolo o gruppo di simboli, per esempio ‘b’, ma solo nel caso che nel sistema sia stata asserita la proposizione ‘a . = . b’ (con . = . indicheremo le identità logiche esplicitamente asserite nel sistema, per distinguerle dalle identità interne ai due membri dell’identità asserita).

III) Se nel sistema compare l’asserzione ‘a = b’, dove ‘a’ e ‘b’ sono simboli o gruppi di simboli, se ‘O’ è un operatore che ha senso applicare ad ‘a’ o a ‘b’, allora anche la proposizione ‘Oa = Ob’ è un’asserzione del sistema.

Con le tre regole precedenti, a partire dalle “proposizioni primitive” del sistema (“definizioni” o “assiomi”), si possono “dedurre” tutte le altre proposizioni del sistema (“teoremi”).

In questo sistema è proibito formare proposizioni della forma a Î a. Tali proposizioni porterebbero a delle contraddizioni, infatti, se sostituiamo Ù al posto della generica classe a otterremmo Ù Î Ù che sarebbe una contraddizione dal momento che per definizione Ù non ha alcun individuo, nemmeno se stesso. Se si esclude tale proposizione per il Ù allora resterebbe la possibilità di definire delle classi che non contengono la classe stessa come individuo (“classi aperte”) e quelle complementari che la contengono (“classi chiuse”) e si arriverebbe al cosiddetto paradosso di Russell:⁸ formiamo la classe degli “aperti”: A . = . '_a (a Ï a) e quella dei “chiusi”: Ã . = . '_a (a Î a). Si ottiene: A Î A . = . A Î Ã, sia che asseriamo che A è aperta, sia che asseriamo che A è chiusa. Il paradosso riposa sulla confusione tra proprietà formali e proprietà reali, cioè non riconoscendo che il termine “classe” esprime solo una proprietà formale e nessuna proprietà reale. È come affermare che “predicato è un predicato” o che “soggetto è un soggetto”!

Quindi nel metalinguaggio si dovrebbe asserire:

( a Î C ) É ((a Î a ) ÏP) ∩ ((a Î ã ) ÏP)

Ma in effetti bisognerebbe asserire una limitazione più forte in modo da escludere la possibilità di formare classi in cui compaiano insieme sia individui che classi formate con tali individui, tutti considerati come individui dello stesso livello.

Non è per niente facile formulare in astratto una tale condizione, tuttavia nei casi concreti della fisica, o di qualunque altra scienza empirica, la cosa risulta sempre banale.

Tale ultima soluzione viene scartata dai metamatematici moderni che vogliono fondare la teoria dei numeri senza fare alcun riferimento alle concrete operazioni fisiche, come proposto da Dedekind e da Cantor e come caldeggiato da Hilbert.

Modernamente, per superare le contraddizioni di tali autori, dovute al fatto che trascuravano la distinzione, introdotta dal Peano, tra le due relazioni Î e É, si accetta di escludere proposizioni della forma x Î x, ma si postula la legittimità di classi della forma a′ = a U ι a , che definisce il successore di un “numero”, avendo identificato un singolo “numero” con un “insieme”. Per cui si ha che per due numeri qualsiasi si può tranquillamente scrivere a Î b e a É b, cosicché, alla fine, la classe dei numeri viene generata tutta intera dall’insieme vuoto e si può ripetere la creazione dal nulla, cosa che prima era riservata solo a Dio e, per di più, si ha che, contemporaneamente, si può avere x Î y e y Î x. È impossibile dare un qualche significato reale a tali asserzioni.

***

Nelle notazioni precedenti abbiamo descritto sinteticamente la “grammatica della logica” o, come equivalentemente si dice l’“algebra della logica”, nel precedente articolo di Boscarino e nell’Appendice di scritti di Peano è sintetizzata la “logica della grammatica” che potremmo anche chiamare l’“algebra della grammatica”, in entrambi i casi si tratta della “forma della forma”.

Tuttavia senza “forma” e senza l’analisi formale di essa non si può parlare del reale.

Si scopre che, con l’uso di tale linguaggio simbolico, si può ricostruire la fisica di quegli antichi scienziati, dei quali ci è pervenuto qualche frammento del loro pensiero o, comunque, qualche testimonianza riportata da scrittori posteriori.

È noto che sumeri ed egizi, fin da secoli molto remoti (XVIII a. C.), possedevano notevoli cognizioni di aritmetica, di geometria e di astronomia, ma le informazioni che si hanno sulla loro fisica sono troppo scarne per poter concludere alcunché, anche se molti scrittori posteriori ad Aristotele fanno risalire ad essi i principi della scienza degli antichi popoli di lingua greca che abitavano la Ionia, la Sicilia e l’Italia meridionale intorno al secolo VI a. C., laddove sono state gettate le basi della nostra scienza.

Le informazioni che abbiamo su questi ultimi sono anch’esse molto scarne e tuttavia ci permettono di formarci un quadro abbastanza coerente del loro modo di intendere la scienza fisica.

Due tradizioni diverse si sono scontrate nel passato, e continuano a confrontarsi insino ad oggi, in relazione ai postulati metafisici, che bisogna pregiudizialmente assumere prima di iniziare lo studio della natura.

Nella prima tradizione, che per brevità chiameremo “empirista”, nata e sviluppatasi prevalentemente tra gli “ionici”,⁹ la realtà fisica viene identificata con il dato dei sensi e tuttavia viene postulato un principio materiale unico che pervade l’intero cosmo. Secondo tale concezione gli oggetti del mondo fisico non sono altro che aggregazioni, più o meno dense, di un tale unico sostrato, che per Talete era l’acqua, per Anassimene l’aria e per Anassimandro una sostanza indefinita. Il movimento era spiegato come una serie di successive condensazioni e rarefazioni di tale sostrato. Oggi chiameremmo tale concezione una “teoria di campo”.

Nella seconda tradizione, che per brevità chiameremo “razionalista”, nata e sviluppatasi prevalentemente tra gli italici, la realtà sensibile è solo apparenza. La vera realtà coincide con la nostra ricostruzione razionale del dato dei sensi, il quale è solo un caos sensoriale da cui nessun principio si può trarre. Gli oggetti del mondo fisico non sono “complessi di sensazioni” (questo termine si deve a Mach che era un ardente sostenitore della concezione empirista della scienza fisica) ma sono definiti solo da determinate proprietà, che prima d’ogni cosa devono soddisfare il principio di non contraddizione. Se di un qualche individuo x noi affermiamo che ha una data proprietà, diciamo a, allora è proibito dire che esso non ce l’ha. Con i nostri simboli: se x Î a allora è impossibile affermare che x Î ã.

Questo porta i pitagorici a formulare la teoria dei contrari e il conseguente principio di dicotomizzazione, il quale, tuttavia, se applicato agli oggetti sensibili, come faceva Platone, porta a conseguenze assurde.

Ma vediamo come si può formulare la teoria degli “italici”, che porta necessariamente a quella che oggi chiameremmo una “teoria di particelle”.

Dal momento che la vera realtà è una pura ricostruzione razionale ne deriva che i termini primitivi del discorso scientifico, li creiamo noi. Questo ci permette e, in un certo senso, ci obbliga ad inventarli in modo che ogni termine possa avere un significato univoco, per cui nel linguaggio scientifico non devono permettersi degli slittamenti semantici e bisogna perciò evitare, finché possibile, i sinonimi e gli omonimi, a meno che, allo scopo di non moltiplicare inutilmente i termini, non ci sia alcun pericolo di provocare ambiguità.

In qualunque nostra proposizione noi, esplicitamente o implicitamente, usiamo il termine “è”, voce del verbo “essere”, allora primariamente dobbiamo chiarire il significato di questo termine e se scopriamo che, nella lingua comune, esso sta per diversi significati bisognerà aggiustare convenientemente il linguaggio scientifico per evitare i paradossi e le contraddizioni.

E così Parmenide pretende che l’“essere” abbia il solo significato di essere pensato astrattamente come logicamente necessario, indipendentemente da qualunque particolare proprietà, e quindi può solo essere “limitato”, in quanto concluso in se, “immobile”, in quanto fisso nella sua identità con se stesso, “omogeneo, isotropo, e senza tempo” in quanto, non avendo altre qualità in nessun modo i suoi elementi possono differire tra loro; in una parola, esso è il “tutto” o, nella terminologia da noi prima introdotta, la “proprietà banale”, il Ú.

La proprietà complementare, il “non-essere”, sarà, per conseguenza, l’“essere contraddittorio”, il “nulla” e, perciò stesso, “impossibile ed inesprimibile” e cioè la “proprietà assurda”, il Ù.¹⁰

Ne possiamo dedurre che, senza introdurre altre proprietà, che siano diverse dall’essere e dal non-essere, il diagramma delle inclusioni, che rappresenta il reticolo delle proprietà, deve essere costituito solo dagli estremi di un segmento, agli estremi del quale possiamo porre i punti Ú e Ù.

Per descrivere il mondo delle apparenze bisognerà allora concepire altre proprietà, e quando ne avremo concepita una, automaticamente con lo stesso atto di pensiero, ne avremo concepito anche quella complementare. Infatti per i pitagorici sono le coppie di contrari che generano tutta la realtà razionale (il logos) e ordinata (il cosmos).

Quando diciamo “spazio fisico” o “materia”, tali nomi non rappresentano enti sensibili, i quali ultimi non sono altro che sensazioni informi e mutevoli, in dipendenza dalle nostre condizioni, anche psichiche ed emotive, di osservazione; essi sono, piuttosto, dei principi logici ordinatori, mediante i quali noi separiamo logicamente la realtà per successive dicotomizzazioni.

Quindi, se introduciamo il termine “natura”, con esso intendiamo parlare di una proprietà che vogliamo contrapporre a tutto il resto; come, p. es., il mondo dei nostri pensieri o dei nostri sogni. E se diciamo che qualcosa esiste in natura, intendiamo semplicemente dire che esiste nello spazio-tempo. E i punti dello spazio-tempo possono essere “materia” o “non materia = spazio vuoto”. Per cui, i punti dello spazio vuoto esistono allo stesso modo dei punti materiali; poiché se dicessimo che non esistono ci ridurremmo di nuovo ad un diagramma delle inclusioni con la sola diade {Ú , Ù}.

Finché non introduciamo altre proprietà la materia resterà indistinta e incapace di rendere la varietà e la complessità delle nostre sensazioni. La prima proprietà che bisogna introdurre è la proprietà dell’estensione, mediante il concetto di distanza tra due punti, di area di una superficie, di volume di un corpo. Queste “grandezze”, indicizzate dai loro rapporti, cioè i “numeri”, sono la vera essenza del mondo.

E, tuttavia, queste proprietà, noi non le traiamo dai nostri sogni o dalle nostre fantasie, ma dalle concrete “operazioni fisiche” che compiamo. Ecco una discriminante importantissima, il mondo reale è sì una nostra ricostruzione logica ma essa viene astratta dalle operazioni concrete fisiche elementari.

Gli elementi sono “operazioni logiche” che rispecchiano (cioè stanno in corrispondenza biunivoca con) le “operazioni fisiche” e quindi non sono fantasmi. È vero che noi possiamo parlare con coerenza formale del mondo iperuraneo o del sesso degli angeli, ma non è di questo che si occupa la fisica, anche se noi, per poter fare riferimento all’empirico, dobbiamo ipostatizzare le particolari proprietà e attribuire ad esse un’“essenza” , fermo restando che il dato dei sensi è mera “apparenza”.

Per cui, gli “enti”, siano essi sensibili o immaginari, non possono costituire gli “elementi”; gli “enti”, al contrario, non sono altro che il risultato ultimo di “relazioni logiche”, e di “rapporti” tra grandezze (λόγος) che sono simboleggiati dai “numeri”.

La natura, cioè il mondo fisico, è caratterizzato dalla proprietà dell’estensione che dicotomizza l’“essere parmenideo” in due classi non nulle: idee di oggetti che hanno estensione e idee di oggetti che non hanno estensione, “essere fisico” ed “essere mentale”. A sua volta l’essere fisico si dicotomizza in “materia” e “vuoto”.¹¹

La fisica di Archimede è un chiaro esempio di tale paradigma.

Secondo i filologi sembra che le prime opere di Archimede fossero state quelle che riguardavano la fisica; da esse sono nate, successivamente, quelle matematiche, ma sempre rivolte alla soluzione di determinati problemi concreti, anche se di natura squisitamente teorica. I due ordini di problemi non erano mai scissi nella sua mente come, chiaramente, emerge dal suo “Metodo Meccanico” per la soluzione di problemi di calcolo di superfici e di volumi di determinate figure; metodo che prelude, in modo di già maturo e consapevole, al calcolo integro-differenziale, anzi, secondo il Peano, la differenza con il calcolo moderno, è solo una questione puramente linguistica e non concettuale.

Si può dire che, per quanto riguarda la statica e la cinematica, niente è stato aggiunto, nei tempi moderni, alle grandi scoperte di Archimede, se non un linguaggio simbolico più funzionale; che, per altro, non è molto recepito nei libri di testo della nostra scuola, se non in una forma parziale e alquanto distorta.

Ad Archimede si rifaranno i fondatori della fisica moderna, con in testa Galilei e Newton, dopo la lunga parentesi della pseudoscienza platonico-aristotelica.

Esaminiamo ora l’evoluzione del paradigma opposto, cioè quello degli ionici; paradigma che, alla fine, sfocerà in due paradigmi diversi che, pur avendo qualcosa in comune, che li distingue dal paradigma che da Pitagora va a Democrito e ai sofisti, hanno, d’altra parte, elementi fortemente divergenti tra loro.

L’elemento in comune è rappresentato dalla netta separazione tra scienza teorica, o “scienza” tout court (essa viene oggi qualificata, invece, come “metafisica”) e arti meccaniche, che oggi si tende a qualificare come “scienze” (al plurale). Il punto di contrasto, tra i due paradigmi, sta nell’oggetto principale di indagine. Contrasto che porta ad una netta divergenza sul ruolo che bisogna assegnare alla matematica.

Così, per Platone, la scienza consiste nell’indagine dell’animo umano dove, scimmiottando i pitagorici, dei quali Platone si dichiarava il vero continuatore, in contrapposto a Democrito e ai sofisti (i quali, d’altra parte, anch’essi sostenevano di essere pitagorici), si illudeva di astrarre un mondo ideale “realmente” esistente ma di assoluta perfezione; solo a questo mondo poteva essere applicata la matematica, scienza pura e incontaminata per eccellenza, e sarebbe stato delittuoso applicarla ad argomenti di meccanica, come si permettevano di fare alcuni suoi amici pitagorici, che pure ammirava e che ricercava, allo scopo di apprendere la matematica (ma sembra che il risultato non sia stato molto proficuo¹²).

Giustamente Aristotele criticava questo presunto pitagorismo, e anche se per costui i pitagorici erano criticabilissimi, tra la teoria platonica e quella pitagorica, mostrava che avrebbe preferito quest’ultima, naturalmente se fosse stato costretto a scegliere.

Quindi il problema della relazione tra mondo del pensiero e mondo dei sensi veniva risolto da Platone negando il problema: si lasci il secondo ai meccanici e occupiamoci del mondo iperuraneo dove solamente possono esistere i numeri ideali e perfetti, le figure geometriche perfette, gli animi perfetti e le repubbliche perfette; e se volete una repubblica terrena, quasi perfetta, affidatela ai filosofi. Mi pare di poter dire che questo genere di platonismo è molto influente nella nostra cultura scientifica, particolarmente nei settori della matematica e anche della fisica teorica, dove, però, si divide il campo con il paradigma aristotelico e tali due atteggiamenti, spesso, convivono nella stessa persona.

Nel paradigma aristotelico, pur convenendosi con Platone che la scienza è cosa ben diversa dalla meccanica, pur convenendosi che la matematica non è utile allo studio della fisica, in quanto gli oggetti della matematica sono perfetti e quelli della fisica non lo sono, anche perché sono in movimento (qui, Aristotele fa eccezione per l’astronomia, per il semplice fatto che in essa predomina, a suo parere, la perfezione che è rappresentata dal moto circolare, proprio delle sfere celesti), tuttavia la fisica in quanto scienza, al pari delle altre scienze empiriche, si deve occupare solo di classificare i fenomeni; gli strumenti per tale tassonomia vengono forniti dalla metafisica con l’ausilio della sua logica, che altro non è che l’analisi grammaticale, alla quale viene aggiunta la chiave universale del sillogismo.¹³

Sbagliano quindi, per Aristotele, i pitagorici a usare numeri e grandezze per ricostruire il mondo, anche se numeri e grandezze, a differenza di quanto pensava Platone, sono molto utili per le arti applicate, da lui poste in un gradino intermedio tra gli interessi del filosofo e quelli del manovale. Un pò di questa metafisica sembra emergere dalle moderne logiche quantistiche, da certe interpretazioni “operazionaliste” della fisica moderna e dalle reinterpretazioni moderne della “fisica classica”.

Da queste brevi considerazioni sulla scienza degli antichi ricaviamo alcune importanti conclusioni:

1) La cosiddetta ‘realtà sensibile’ non è la “Realtà” ma pura “Apparenza”, illusione creata dai nostri sensi, come ben diceva Parmenide.

2) La “Realtà” è la ricostruzione razionale della realtà sensibile mediante le regole “formali” della logica, costruite mediante una coerente “Astrazione” dalle nostre operazioni fisiche elementari ricostruibili sulla carta con strumenti elementari come riga e compasso, ecc.

3) Dal momento che la realtà sensibile è troppo complessa e mutevole da istante a istante, come riconosceva Eraclito, la sua ricostruzione razionale può avvenire solo mediante un processo di “Idealizzazione” mediante l’invenzione di opportune “idee” o “elementi” o “atomi” cuciti insieme in un “Reticolo” matematico di inclusioni logiche. Solo tale ricostruzione soddisfa la nostra “Ragione”, ma naturalmente non ci dà nessuna emozione.

4) Per ricostruire nella nostra “Memoria” le emozioni della nostra esperienza passata (oggi bisogna includere le “esperienze virtuali” create con mezzi informatici!) bisogna ricorrere alla “Poesia” che, in quanto tale, si affranca dalle regole della grammatica e anche della logica ma anch’essa ha la sua algebra che opera sugli “elementi” della fantasia e del sentimento.

5) Chi confonde la Forma con la Realtà non può fare né scienza né poesia, ma solamente chiacchiere inutili.

NOTE

1. S. Notarrigo, Il linquaggio scientifico dei Presocratici analizzato con l’ideografia di Peano, in Ripensando Peano e la sua scuola, Quaderni di Mondotre, suppl. ai N. 4 – 5, ottobre 1989. TORNA

2. S. Notarrigo, Archimede e la fisica, Atti del convegno Archimede-Mito, Tradizione, Scienza, Siracusa – Catania, 9 - 12 ottobre 1989, a cura di C. Dollo, Ed. Olschki, Firenze, 1992, pag. 381. TORNA

3. Le precedenti e seguenti distinzioni ed esempi si devono al grande matematico italiano Giuseppe Peano, che in modo insuperabile ha condotto a termine il sogno di Leibniz al quale prima abbiamo accennato. TORNA

4. Oggi per quest’ultima relazione vengono impiegati diversi simboli, come =, º, «, Û, ciò si fa allo scopo di distinguere l’identità logica da altre forme di equivalenza; ma spesso molti autori usano scambiare il significato dei simboli, nel senso che alcuni usano = per l’identità logica e º per un’equivalenza generica e altri fanno il viceversa e così via. Naturalmente non c’è niente di male nel far questo, dal momento che i vari segni non significano niente per se stessi, ma significano solo per le nostre convenzioni linguistiche. Tuttavia sarebbe estremamente utile una convenzione internazionale. Noi, seguendo Peano, useremo lo stesso simbolo per i due significati. Il significato appropriato emergerà sempre chiaramente dal contesto. TORNA

5. Notiamo che oggi quasi tutti usano, invece, i simboli Ì o Í . Noi seguiremo la scelta di Peano, per le ragioni che emergeranno in seguito. TORNA

6. Notiamo, tuttavia, che i logici moderni, seguendo Russell, operano con il simbolo $ sull’individuo invece che sulla classe e scrivono $ x a(x) che leggono “esiste un individuo x e x ha il predicato a”. Ma noi preferiamo seguire Peano perché, in realtà, in questo caso, non si fa nessuna affermazione su di un individuo, ma soltanto su di una classe: infatti, proviamo a porre x = Socrate e a = filosofo, ne verrebbe che: “esiste un individuo Socrate e Socrate ha il predicato filosofo”. La proposizione si trasforma in due asserzioni, di cui una esistenziale, al di fuori della portata della logica, e l’altra qualificativa, che è lontana dall’affermazione puramente logica con la quale si voleva semplicemente dire che non è assurdo il pensare che vi siano individui che possano essere filosofi. Questo semplice cambio di scrittura, apparentemente banale, ha provocato infinite discussioni accademiche sul significato di “esistenza” e ha fatto nascere altri rami della logica (?!), chiamate “logiche libere”, cioè prive di quello che viene chiamato “quantificatore esistenziale”, $ x, riferito all’“individuo” x: nei fatti si tratta solo di vacui formalismi pseudogrammaticali. TORNA

7. Anche il simbolo si fa operare, dai seguaci di Russell, sugli individui invece che sulle classi: essi introducono il “quantificatore universale”, ", e scrivono ~ $ x ã (x)= " x a(x) , che leggono “per ogni individuo x, x ha il predicato a”. TORNA

8. Russell fu condatto a tale paradosso nel fallito tentativo di conciliare la dimostrazione di Cantor circa l’impossibilità che esista un numero cardinale massimo con la sua personale ipotesi, successivamente abbandonata, che la classe di tutti i termini debba necessariamente avere il massimo numero possibile di individui. TORNA

9. Con il termine “ionici” intenderemo quella scuola di pensiero che si fa nascere con Talete e nella quale Diogene Laerzio, indipendentemente dalla provenienza geografica dei singoli pensatori, pone anche Platone ed Aristotele. Allo stesso modo, con il temine “italici” intenderemo sia i pitagorici che la scuola di Elea: fra gli italici Diogene Laerzio pone anche i pensatori della scuola degli atomisti, compresi Democrito ed Epicuro. TORNA

10. Dai frammenti di Parmenide: “…bisogna che il dire e il pensare sia l’essere: è dato infatti essere mentre nulla non è…allontanati da coloro che nulla sanno e vanno errando, gente dalla doppia testa: perché è l’incapacità che nel loro petto dirige l’errante mente: ed essi vengono trascinati insieme sordi e ciechi, istupiditi, gente che non sa decidersi, da cui l’essere e il non essere sono ritenuti identici, per cui di tutte le cose reversibile è il cammino.”. TORNA

11. Simplicio riporta una citazione di Aristotele in cui si legge: “Democrito ritiene che la materia di ciò che è eterno consiste in piccole sostanze infinite di numero; e suppone che queste siano contenute in altro spazio (cioè diverso da quello occupato dalla materia stessa), infinito per grandezza; e chiama lo spazio coi nomi di “vuoto” e di “niente”(=non-ente) e di “infinito”, mentre dà a ciascuna delle sostanze il nome di “ente” e di “solido” e di “essere”. Egli reputa che le sostanze siano così piccole da sfuggire ai nostri sensi: esse si muovono nel vuoto …e si incontrano legandosi nel contatto reciproco per un certo tempo, egli dà la causa ai collegamenti e alle capacità di adesione degli atomi.. ed essi si tengono attaccati gli uni agli altri e rimangono in contatto solo fino a quando, col sopraggiungere di qualche azione esterna, una necessità più forte non li scuota violentemente e li disperda in varie direzioni”. TORNA

12. “Alcuni autori attribuiscono a Platone degli studi sugli irrazionali (Baltzer, Elem. d. Mathem. a. 1885 p. 100; Encyclop. P. 49). Invero nei dialoghi di questo filosofo trovansi qua e là dei termini matematici, ma riuniti in modo così incerto da farli ritenere come parole difficili con cui un interlocutore cerca confondere l’avversario: all’incirca come nei giornali politici del giorno d’oggi sta scritto incommensurabile invece di grandissimo. Il passo più volte citato, nella Πολιτεία VIII 546 è considerato dai commentatori Jowett and Campbell, Oxford a. 1894, come un riddle. Al più da un passo del Θ ε α ìτ ή τ ο ς 143 E, si può dedurre , e ciò parmi la cosa più importante contenuta in quelle opere su questo soggetto”, tratto da: G. Peano, Opere scelte, vol. III, Ed. Cremonese, Roma, 1958, p. 249. TORNA

13. “È noto che la Logica scolastica non è di sensibile utilità nelle dimostrazioni matematiche: poiché in queste mai si menzionano le classificazioni e le regole del sillogismo…”, ibidem, II, p. 80 e nel Dizionario di Matematica: “Logica matematica è la scienza che tratta delle forme di ragionamento che si incontrano nelle varie teorie matematiche riducendole a formule simili alle algebriche. Essa ha a comune alla logica d’Aristotele il solo sillogismo. Le classificazioni dei vari modi di sillogismi, quando sono esatte, hanno in matematica poca importanza. Nelle scienze matematiche si incontrano numerose forme di ragionamento irreduttibili a sillogismi.”, tratto da: ibidem, II, p. 379. TORNA