GEOMETRIA
E FISICA
G. Boscarino, S. Notarrigo, A. Pagano
Gruppo
Nazionale di Storia della Fisica Ś UnitÓ di Catania
Comunicazione presentata al Convegno Nazionale su
Peano e i
fondamenti della Matematica, Modena. 22-24 Ott. 1991.
Organizzato dallÆAccademia Naz.le di Scienze,
Lettere ed Arti di Modena
La filosofia di Peano
╚ noto come Peano, con la sua ōideografiaö , abbia portato a
compimento i1 sogno di Leibniz, relativo ad un linguaggio scientifico, privo di
ambiguitÓ, capace di arrivare alle conclusioni per mezzo di un semplice calcolo
simbolico.
Ma Ķ anche noto come lo stesso Peano sia
stato tagliato fuori dalle innumerevoli, e a nostro giudizio poco fruttuose,
discussioni sulla cosiddeta crisi dei fondamenti della matematica.
Alcuni pensano che sia stato lo stesso Peano
ad estraniarsi dalla battaglia in corso, ma noi propendiamo verso
unÆinterpretazione che assegna agli altri il merito o il demerito (a seconda
dei punti di vista, noi siamo per il demerito!) di averlo escluso.
A leggere gli interventi di Peano, cosņ come
raccolti nelle sue ōOpere Scelteö,1 non cÆĶ argomento rilevante ai fini di
una discussione, che necessariamente pu“ solo essere filosofica, sui fondamenti
della matematica, che non sia stato da lui affrontato e, a nostro parere, anche
risolto!2
╚ da riconoscere, per“, che raramente si pu“
trovare in tali scritti un qualche riferimento agli argomenti che, almeno cosņ
a noi sembra, pi∙ appasŁsionavano partecipanti alla disputa. Argomenti che,
tuttavia, sono ancora i principali ingredienti dellÆodierna metamatematica.
Nasce, allora, il problema di capire
lÆessenza della filosofia di Peano che, necessariamente, doveva essere cosņ
dissimile dalle altre che si contendevano il campo, in apparente aperto
contrasto tra loro.
Parliamo di contrasto solo apparente perchķ
una particolaritÓ le accoŁmunava e che drasticamente le differenziava dalla
filosofia di Peano.
La particolaritÓ in comune, tanto per darle un
nome, la chiamiamo ōmodernismoö,
in quanto opponentesi al ōclassicismoö
difeso dal Peano.
Il paradigma del modernismo si era
manifestato, giÓ molto tempo prima, come del resto Ķ ovvio che doveva essere,
nella letteratura, nella filosofia senza altri aggettivi, e successivamente
nelle scienze, prima fra tutte nellÆeconomia politica, ed ha poi investito
tutte le altre scienze, logica, matematica e fisica comprese.3
Ma non vogliamo qui toccare questi punti atti
a far degenerare ogni discussione, caricandola di emozioni di non facile
controllo. Del resto, lÆanaŁlisi di questi rivolgimenti Ķ stata fatta da molti,
a partire da Marx, ed Ķ oggi opinione quasi generale che le cause sono da
ricercare fuori dal contesto puramente scientifico, essendo rilevanti ed
essenziali i fattori socio-economici.
Quindi ci limiteremo a fare un discorso un
poÆ pi∙ neutrale e pi∙ adatto allÆAccademia di cui, peraltro, siamo parte.
CÆĶ un punto sul quale tutti si dichiarano
dÆaccordo: cÆĶ il mondo dei sensi e cÆĶ il mondo della ragione. Ma lÆaccordo
cessa immediatamente quanŁdo si tratti di stabilire in che misura il discorso
scientifico debba fare appello allÆuno o allÆaltro dei due mondi. La
discussione su questo dilemma diventa, parafrasando Popper, un terzo mondo.
Le risposte a tale problema sono sempre state
le pi∙ varie fin dai tempi pi∙ antichi;4
e sempre hanno oscillato fortemente tra due posizioni estreme, lÆuna che
identifica la realtÓ con il mondo delle sensazioni informi (il caos), lÆaltra
con il mondo ordinato per mezzo della ragione (il cosmos).
Le posizioni di compromesso sono sempre
apparse difettose e non coerenŁti, specialmente nella fisica e nelle altre
scienze che devono fare riferimento ai fatti empirici; ma, anche, nella logica
e nella matematica.
Esaminiamo, p. es., le posizioni
epistemologiche di Einstein. Da un lato egli fa appello ad una particolare
interpretazione del cosiddetto metoŁdo ōipotetico-deduttivoö,
che secondo lo stesso Einstein dovrebbe ricevere la sua validitÓ, solamente
a posteriori, dalla verifica empirica delle conseguenze matematiche delle
ipotesi; ma, dallÆaltro lato, per giustificare le sue ipotesi fa appello, a
priori, a dei fatti empirici complessi, difficilmente analizzabiŁli in termini
di ōelementiö, intesi come quei
mattoni, i pi∙ adatti, per la costruzione dellÆedificio teorico.5
Un altro tipo incoerente di compromesso fa
appello ad unÆerrata inŁterpretazione del cosiddetto ōoperativismoö di Bridgmann, nella falsa idea che, a partire dalle
grandezze operativamente definite e dalle relazioni tra di esse empiricamente
trovate, si possa costruire una teoria matematica onŁnicomprensiva, come, p.
es., capita nella pi∙ popolare interpretazione della meccanica quantistica.
Lo stesso problema si ripresenta, anzi si era
giÓ prima presentato, nella matematica e nella logica. Il problema dei
fondamenti della matematica e degli assiomi della logica, a nostro avviso, non
consiste, e non Ķ mai consistito, nel cercare i mattoni pi∙ adatti, ma quello
di decidere preventivamente lÆuso che se ne voleva fare.
Se la matematica dovesse solo servire ad
organizzare il discorso delle altre scienze, allora il problema dei fondamenti
non si porrebbe affatto. Basterebbe usare la medicina giÓ proposta da Peano6:
ōģLÆanalisi
del concetto di moto e la determinazione
dei postulati fonŁdamentali, si pu“ fare seguendo la solita via. Si scrivano
tutte le proprietÓ che risultano dallÆosservazione del moto fisico.
Si scindano queste proposizioni in tante affermazioni semplici; e poi
si esamini quali di queste affermazioni sono giÓ implicitamente contenute nelle
rimanenti. Procedendo avanti in questo esame, finchķ sarÓ possibile, troveremo
un gruppo di affermazioni esprimenti veritÓ irriduttibili tra loro, e che
costituiscono i postulati del motoģö.
Qui Peano si riferisce al moto fisico ma la
stessa ricetta, lÆaveva suggerita con parole solo leggermente diverse, e,
soprattutto, lÆaveva concretamente usata, per determinare i postulati della
geometria, dei numeri e, persino, della logica:7
ōģNel
Formulario, la logica matematica viene adoperata esclusivamente come strumento
per esprimere e trattare le
proposizioni della matematica usuale; e non Ķ fine a
se stessa; essa viene spiegata in 16 pagine; unÆora di studio Ķ sufficiente per
sapere tutto quello che Ķ necessario
per applicare la nuova scienza della logica alla matematicaģö.
Per cui gli stessi assiomi dei numeri interi8 vengono ōas trattiö con lo stesso metodo sopradescritto (Peano, dice, pi∙
precisamente che se ne defiŁniscono le proprietÓ per mezzo di una ōdefinizione per astrazioneö)
a partire dalle operazioni elementari che compiamo nel misurare le
grandezze fisiche per confronto diretto.
Ma, per chi volesse ōliberareö la matematica dalla schiavit∙ verso la fisica, come
hanno voluto fare Cantor e Dedekind,9
abbandonando definiŁtivamente il supporto delle grandezze fisiche,
bisognerÓ pur che trovi una soluzione al problema della coerenza degli assiomi!
Specialmente quando si volesse continuare a parlare dellÆōinfinitoö e
degli ōinfinitesimiö10.
Ma al programma hilbertiano, come tutti
dicono, Ķ stata sbarrata la via dal G÷del, ed allora si ricorre a sotterfugi
formali che, sul piano dei signiŁficati, ammontano semplicemente a ripristinare
lÆambiguitÓ tra due ōideeö ben diverse che Peano aveva
nettamente distinto introducendo due diversi simboli, ╔ e ╬ .
Vediamo, invece, come Peano risolve il
problema dei fondamenti della logica, della matematica e della fisica, tutte
insieme.
La sua soluzione pu“ essere riassunta col
dire: non cÆĶ niente da camŁbiare o da inventare sulle grandiose conquiste di
Democrito, Eudosso, EucliŁde, Archimede, Galilei, Newton. Resterebbe solo da
inventare un linguaggio (o meglio, unÆōideografiaö) adeguato per poterle
esprimere senza alcuna ambiguitÓ. Il suo calcolo simbolico Ķ perfettamente
adeguato e sufficiente.
Ma qual e la comune filosofia di questi
illustri scienziati che abbiamo nominato?
1) Logica,
matematica e fisica non sono separabili e sono la ōscienzaö.
2) Il
linguaggio della scienza non puo essere il linguaggio comune, nĶ una sua
semplice estensione, in quanto, il primo fa riferimento al ōcosmosö, creato dalla ragione ed il secondo al ōcaosö, prodotto dalle sensazioni.
3) Il
contatto tra i due linguaggi Ķ necessario allÆinizio del processo di costruzione
della teoria, allo scopo di poter determinare gli assiomi, ma sempre a partire
dalle pi∙ semplici ed elementari operazioni fisiche; ed Ķ ancora necessario
alla fine, per la spiegazione dei fatti empirici, siano questi il prodotto di
semplici osservazioni o di raffinati esperimenti. Per determinare gli assiomi
non si pu“ partire, da fenomeni complessi, la spiegazione dei quali, invece,
deve essere proprio il risultato finale della teoria.
4) La coerenza della teoria, sia essa logica,
matematica o fisica, Ķ assicuŁarata dalla adeguatezza degli assiomi alle
fattibili operazioni fisiche elementari. LÆindipendenza di ogni singolo assioma
si pu“ solo accertare se vi sono moŁdelli fisici concreti e funzionanti che
obbediscano a tutti gli altri assiomi della teoria ma falsificano quello di cui
se ne vuole provare lÆindipendenza. Per quŁanto riguarda la completezza,
nessuno potra mai sapere nemmeno cosa mai significhi, se non in relazione ad un
determinato campo fenomenico.
Con tali ricette, gli antichi non potevano
mai inventare la metamatemaŁ tica, dal momento che non ne sentivano il bisogno.
Si pu“ concludere, anche, che gli antichi, e
Peano con essi, non sentivano il bisogno della ōfisica matematicaö, intesa come la matematizzazione della
fisica; dal momento che, in modo del tutto naturale, andavano sviluppando una ōmatematica fisicaö,
cioĶ quella matematica modellata sulle operazioni fisiche, e non riuscivano
a concepire nessun altro tipo di matematica, specialmente di quella che si fa
discendere dagli imperativi deontologici che nascono dalle filosofie platoniche
o aristoteliche.
Il calcolo geometrico di Peano
Come illustrazione delle tesi qui sostenute,
mostriamo ora alcune conseŁguenze che si possono tirare dallÆimpostazione del ōCalcolo Geometricoö di Peano.
Peano fa risalire a Leibniz il primo
tentativo nella direzione di unÆalŁgebrizzazione degli enti geometrici, che non
facesse uso della intermediazione delle coordinate, e nota che,
successivamente, sono state sviluppate diverse specie di calcolo geometrico.
I pi∙ interessanti, a suo giudizio, sono il Calcolo baricentrico di M÷bius (1827),
quello delle Equipollenze di
Bellavitis (1832), quello dei Quaternioni
di Hamilton (1853) e, infine, il calcolo geometrico del Grassmann (1844),
questÆultimo basato sul concetto di ōforma
esternaö e di ōprodotto esternoö tra
forme.
Tuttavia tali opere, la cui importanza solo
recentemente comincia ad esŁsere riconosciuta in alcuni settori della fisica
matematica, non hanno trovato, fino ai nostri tempi, molto favore, nķ tra i
fisici, nĶ tra i matematici.
Maxwell si permise di usare il calcolo
quaternionico di Hamilton nel suo famoso trattato sulla teoria
dellÆelettromagnetismo; ma, da un lato, si Ķ limitato ai quaternioni retti (che
oggi si usa, impropriamente, chiamare vettori) e, dallÆaltro, li ha usati nel
linguaggio delle coordinate, sminuendone, cosņ, la portata innovativa.
Come Ķ noto, intorno al 1888, tutta la
materia Ķ stata ripresa dal PeŁano,11
semplificata nella forma e nei simboli e unificata sulla base del pi∙
comprensivo calcolo del Grassmann; ma, soprattutto, riscritta in forma ōasŁsolutaö, cioĶ in modo
indipendente da qualunque sistema di coordinate e da qualunque sistema di unitÓ
di misura.
Ma nemmeno tale importantissima opera ebbe
successo, se non in miniŁma parte e ad opera di alcuni collaboratori del Peano
che hanno estratto, dal sistema completo di calcolo, quello che essi chiamavano
ōil sistema minimoö,
che oggi Ķ universalmente conosciuto come calcolo vettoriale.
Tuttavia tale calcolo, impostosi in passato
soprattutto tra i meccanici raŁzionali, veniva accettato solo nella sua forma
simbolica, ma, sostanzialmente, tradito nei suoi intendimenti, quali venivano
ōpropugnatiö dai suoi principaŁli sostenitori, come Burali-Forti, Boggio,
Burgatti, Marcolongo, Bottasso, Pensa, ecc. che condussero una lunga battaglia
con scritti fortemente poleŁmici.
Il succo di tale polemica ha una notevole
rilevanza per i metodi e il ruolo della fisica teorica.
NellÆidea di Peano e dei suoi collaboratori,
il calcolo aveva valore in quanto si poteva con esso parlare della realtÓ cosņ
come ce la rappresentiamo nella nostra mente. Gli enti di cui parliamo (punto,
retta, segmento, massa, forza, ... ), noi li pensiamo indipendentemente dal
sistema di coordinate; e i numeri che esprimono il risultato delle nostre
misure sono solo lÆultimo atto; tali misure vengono effettuate sempre in
relazione a ben determinati sistemi di riferimento che sono i pi∙ vari, a
seconda del caso concreto, e spesso non i pi∙ semplici dal punto di vista della
matematica.
Se una relazione vale per gli enti, essa deve
valere in tutti i possibili sistemi di coordinate e per tutti i possibili
sistemi di unitÓ di misura, e quindi la notazione deve essere tale da non avere
bisogno di una tale esplicita simbolizzazione, la quale, invece, risulta
assolutamente necessaria quando la relazione viene espressa mediante le
coordinate.
La maggior parte degli utenti, invece,
accettava le relazioni tra simŁboli (rappresentanti gli enti) come semplici ōtachigrafiö delle coordinate, e
riconosceva come reali solo le ōmisureö, almeno a parole, ma nei fatti solo
i ōnumeriö, confondendo le ōmisureö con le ōmisurazioniö; cose tra le quali esiste una differenza
concettuale incolmabile, in quanto le prime sono semplici numeri e le seconde,
invece, ben determinate operazioni fisiche. Alcuni effetti di tale confusione
si registrano nella attuale (ma nello stesso tempo antichisŁsima) problematica
relativa ai concetti di spazio, tempo e movimento.
Negli ultimi tempi, alcuni fisici matematici,
ognuno per conto suo e fuori dal paradigma dominante, sono andati riscoprendo
chi il calcolo quŁaternionico di Hamilton, chi, e sono i pi∙, il calcolo delle ōforme esterneö del Grassmann; ma, ancora
una volta, nel linguaggio delle coordinate (quando non Ķ possibile farlo
globalmente si ricorre a ōcarteö e ōatlantiö) e lÆaggettivo ōassolutoö (sempre lui!), che dai
peaniani (chiamiamoli cosņ) veniva inteso coŁme ōindipendente dal sistema di coordinate presceltoö (che comprende
anche lÆassegnazione delle unitÓ di misura prescelte) ora viene inteso come ōindipenŁdente dallo spazio euclideo in cui
pu“ sempre essere immersoö che, automaŁticamente (e senza ragione), si
traduce con ōeventualmente non-euclideoö,
dal momento che non si fa pi∙ il benchķ minimo riferimento alle unitÓ
diĀ misura12.
Va notato, tuttavia, che questi approcci moderni (ma, piuttosto, biŁsognerebbe dirli antichi anche se sconosciuti) allo studio della meccanica hamiltoniana rappresentano un notevole progresso metodologico rispetto ai metodi che ancora si ritrovano su quasi tutti i libri di testo di meccanica classica, dove lo spazio delle fasi viene assimilato ad uno spazio euclideo; quando che, invece, non Ķ assolutamente possibile definirvi alcun concetto di distanza.
Nei nuovi approcci, si dice che un sistema
hamiltoniano viene descritto nello spazio delle fasi, il quale ha struttura di ōvarietÓ simpletticaö, la quale ultima viene contrapposta
alle ōvarietÓ riemannianeö. Ma poi si
continuano tranquillamente a sommare impulsi con coordinate o anche vettori con
mulŁtivettori di qualunque grado, come si pu“ vedere, p. es., nei libri citati
nella nota successiva.
Strana situazione questa: si chiamano non
euclidei degli spazi (?), che si possono sempre immergere nello spazio fisico
(sempre euclideo per le deŁfinizioni di distanza, di area e di volume) e si
fanno diventare euclidei degli spazi (?) che non lo possono mai essere se il
termine ōgrandezza fisicaö deve continuare
ad avere un qualche senso!
Data lÆartificiositÓ e lÆastrattezza di
questi approcci moderni alla meccanica13,
pensiamo che, almeno nella didattica, sia preferibile riprendere lÆarŁgomento a
partire direttamente dal livello, giÓ abbastanza alto, raggiunto dal Peano.
Peano cerc“ di fare un poÆ di propaganda in
favore del suo calcolo geŁometrico per gli usi della fisica; ma, come Ķ ben
noto, fu bruscamente fermato, anche a causa della ben nota polemica col
Volterra.
Nella sua prima esposizione, giÓ citata nella
nota 11, Peano vi fa preceŁdere un capitolo sui simboli della
logica, che, a quella data, non hanno ancora raggiunto la maturitÓ che si
ritroverÓ poi nel ōFormularioö;
e, per gli enti geometrici, usa dei termini che saranno successivamente
modificati nel ōForŁmularioö,
probabilmente per evitare di confonderli con i diversi significati che,
agli stessi termini, venivano usualmente attribuiti.
Per tale ragione, noi useremo i termini del ōFormularioö e, dato il nostro scopo, ci
permetteremo di modificare lÆordine della presentazione ed alcuni simboli, e
anche di estenderne le conseguenze dal punto di vista della fisica, ma sempre
nello spirito della filosofia di Peano, come sopra lÆabbiamo deliŁneata; ma,
naturalmente, senza dare dimostrazioni, per le quali rimandiamo alle opere di
Peano e dei suoi collaboratori.
Ma, prima di tutto, faremo uso delle ōideeö (cioĶ dellÆōideografiaö,
ma senza la ōgrafiaö!)
di Peano per ricostruire lÆidea della meccanica che, a nostro giudizio, si
era andata sviluppando negli ambienti pitagorici, per arrivare alla sintesi
archimedea, alla quale fa esplicito riferimento il Galilei, per poi culminare
nella grandiosa opera di Newton, il quale sembra, addirittura, che attribuisse
ai pitagorici la stessa idea della legge dellÆinverso del quadrato delle
distanze.14
Partiamo dalla teoria dei contrari o, in
linguaggio moderno, delle proprietÓ complementari, come professata dai
pitagorici, che esporremo alla luce delle precisazioni parmenidee e con lÆaiuto
dellÆideografia peaniana.
Per i pitagorici la realtÓ Ķ niente altro che
la ricostruzione razionale delle impressioni sensoriali che sono solo
apparenza. Noi, certamente, inventiamo le proprietÓ a partire dal dato dei
sensi ma poi, nella ricostruzione razionale, sono le proprietÓ che devono
costituire lÆōelementoö primario,
il ōprincipioö. Gli individui possono
solo essere definiti per mezzo di esse, e non viceversa, come in seguito hanno
potuto pensare Aristotele e Russell (per citare solo i capiscuola pi∙
influenti).
Se di qualche individuo asseriamo
semplicemente che Ķ, abbiamo sempliŁcemente enunciato la banalitÓ, che lÆunica
proprietÓ che lo caratterizza Ķ quella di ōessereö,
nel senso parmenideo del termine. Ma questa Ķ propro lÆunica proprietÓ il
cui complemento non pu“ avere individui. In altre paŁrole la proprietÓ
complementare dellÆōessereö Ķ niente altro che la proprietÓ assurda, il ōnullaö di Parmenide.
Quindi, ogni altra proprietÓ, se non Ķ quella
banale di ōessereö o quella assurda
di ōnon essereö,
deve essere non vuota e anche la sua complementare deve essere non vuota.
Per brevitÓ, nel seguito, indicheremo
lÆessere con il simbolo ┌, e il non essere con ![]() .
.
Se inventiamo la proprietÓ di ōessere fisicoö ed asseriamo che essa
non coincide nķ con ┌, nķ con ┘, devono necessariamente esistere individui
non fisici. Per caratterizzare gli individui fisici, assegnamo ad essi la
proprietÓ delŁlÆestensione, che possiamo definire geometricamente mediante una
relazione tra gli individui dellÆessere fisico.
Per caratterizzare ulteriormente lÆessere
fisico, facciamo unÆaltra dicoŁtomizzazione inventando la ōmateria=ente=atomoö e la ōnon
materia=non ente=niente=vuotoö; attribuendo alla materia il movimento.
Gli individui dellÆessere fisico li chiameremo ōpuntiö, quelli
della materia ōpunti materialiö. Un ōcorpoö Ķ un sistema di punti materiali.
Consideriamo un corpo di N ōpunti materialiö dello spazio fisico, che indichiamo con ![]() Ā(i=
1,2...,N).
Ā(i=
1,2...,N).
Porremo ![]() Ā,
essendo miĀ la
ōmassaö di
Ā,
essendo miĀ la
ōmassaö di ![]() Āe PiĀ
il ōpunto geŁometricoö in cui immaginiamo localizzata la
massa.
Āe PiĀ
il ōpunto geŁometricoö in cui immaginiamo localizzata la
massa.
Chiamiamo ōsistema meccanicoö lÆinsieme
di tali punti materiali.
Indicheremo tale sistema con la scrittura:
(*)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀ ![]() ĀĀĀ.
ĀĀĀ.
Il sistema costituito da due soli punti
materiali ![]() ,
, ![]() , sara:
, sara:
![]() Ā .
Ā .
Il significato del segno + e del segno di
sommatoria nella (*), Ķ conŁvenzionale,
tuttavia supporremo che tale operazione goda della proprietÓ ōcommutativaö
e della proprietÓ ōassociativaö:
![]() Ā ,
Ā ,
![]() Ā ,
Ā ,
Faremo pure lÆipotesi:
mi Pi = Pi miĀ .
Permetteremo, naturalmente, che un sistema
meccanico possa anche esŁsere costituito da un solo punto materiale.
Se ![]() Ķ un sistema meccanico di N
punti materiali,
Ķ un sistema meccanico di N
punti materiali, ![]() , scrivereŁmo, per esso, anche:
, scrivereŁmo, per esso, anche:
![]() Ā.
Ā.
Chiameremo ![]() , la
ōmassa del sistemaö e
, la
ōmassa del sistemaö e
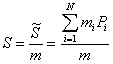 Ā ,
Ā ,
il ōbaricentro del sistemaö.
Daremo significato al prodotto di due punti
geometrici A, B,
e lo scriveremo semplicemente AB,
sottintendendo il segno dellÆoperazione prodotto.
IlĀ significato
di AB sarÓ per noi:
ōAB ķ un
segmento di retta limitato dai punti A e B e orientato da A verso Bö.
Lo chiameremo semplicemente ōbipuntoö.
La lunghezza di AB la indicheremo con | AB | = | BA |.
Da questa definizione ne viene che il nostro
prodotto deve essere ōanti-commutativoö, cioĶ:
AB
= ¢ BAĀ ,
ma assumeremo che sia anche ōassociativoö:
A(BC) = (AB)C = ABCĀ ;
per cui daremo significato anche al prodotto di tre punti:
ōABC Ķ il
triangolo di vertici A, B, C e di area | ABC | che pensereŁmo orientata, immaginando che tale area venga descritta da
AP con P che descrive BC da B verso Cö.
Lo chiameremo ōtripuntoö.
Questa regola di orientazione viene ad essere
dÆaccordo con lÆanticommutativitÓ del prodotto tra punti:
ABC = ¢ BAC
= BCA.
Analogamente, possiamo dare significato anche
al prodotto di quattro punti:
ōABCD ķ il
tetraedro di vertici A, B, C, D e di volume | ABCD |, che penseremo orientato, immaginando che tale volume venga descritto
da ABP con P che descrive CD da C verso Dö.
Lo chiameremo ōquadripuntoö.
Se il nostro spazio Ķ lo spazio fisico, esso
avrÓ solo tre dimensioni e quindi converremo che il prodotto di cinque o pi∙
punti sia sempre nullo.
Converremo, anche, che il rapporto tra due
quadripunto sia un numero reale che rappresenti, in valore e segno, il rapporto
tra i volumi dei due tetraedri corrispondenti.
Allora, ōfissato un volume unitarioö,
secondo le convenzioni sui sistemi di misurazione coerenti, ABCD pu“ rappresentare, a seconda dei
casi, sia il volume orientato che il numero che ne costituisce il valore.
ABCD
= 0 significherÓ, allora, che i
quattro punti sono ōcomplanariö.
E quindi, significherÓ anche: A giace nello stesso piano di BCD; le rette su cui
giacciono, rispettivamente, AB e CD si incontrano in un punto o sono
parallele, e cosņ via di seguito.
Diremo che due quadripunto sono uguali se i
loro volumi orientati sono uguali, cioĶ, quando, essendo u il volume
unitario, si ha, per definizione:
![]() Ā .
Ā .
Quindi, il segno =, posto tra i due quadripunto, non si deve intendere come unÆidentitÓ logica, ma come unÆequivalenza che fa riferimento solo ai volumi orientati e non alla posizione effettiva dei tetraedri nello spazio fisico.
Perci“, ha senso sommare due quadripunto per
ottenere un terzo quadri punto, che pu“ essere nullo, nel caso che i due
quadripunto abbiano volumi eguali ma siano di segno opposto.
In altre parole, ponendo lÆunitÓ di volume =
1, i quadripunto si comporŁtano come dei numeri reali.
Ed ha senso una loro qualsiasi combinazione
lineare:
(**)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀ ![]() ĀĀĀ,
ĀĀĀ,
dove v e
i vi Āsono quadripunto e gli ai Āsono dei numeri reali.
Dalle precedenti convenzioni deduciamo che se
A Ķ un tripunto e A e
B sono punti, allora
lÆuguaglianza:
AA Ā= BA
significherÓ che AB Ķ
parallelo adA . Cosņ,
AA ĀĀĀ> 0
ĀĀĀĀĀĀĀĀĀĀ BAĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ .
significherÓ che A e B
stanno dalla stessa parte rispetto al piano su cui giace A ; e,
se il rapporto precedente Ķ invece negativo, allora A starÓ da una parte e B dallÆaltra
rispetto al detto piano.
Se α e β sono
bipunti, ovviamente sarÓ:
αβ = βαĀĀ ;
cioĶ, il prodotto tra bipunti Ķ commutativo.
Per definizione,ĀĀ diremo che un tripunto,Ā A ,Ā ĀĶ
nullo (A = O),Ā se qualunque sia il punto P, si ha
A P=0ĀĀ .
Il che significa che lÆarea del triangolo
corrispondente Ķ nulla; se A = ABC =
0 i tre punti A, B, C, sono ōcollineariö, cioĶ,
stanno sulla stessa retta; se α e un bipunto, Aa = 0 , significa che il punto A giace sulla retta su cui giace α.
Per definizione, diremo che due tripunti sono
uguali (A = B Ā) se per qualunque punto P si ha:
A P= B ĀP .
Dal che si deduce che condizione necessaria e
sufficiente affinchķ due tripunti siano uguali Ķ che giacciano sullo stesso
piano e che abbiano la stessa area orientata, indipendentemente dalla loro
posizione relativa nel loro piano.
Se A e
B sono punti e α Ķ un
bipunto, lÆuguaglianza
α A = α BĀ ,
significherÓ che α e AB
sono paralleli.
Un bipunto α si dice nullo (α
= 0) se, qualunque sia il bipunto ξ si ha: α ξ = 0.
Se ne deduce che la lunghezza del segmento Ķ
nulla; o, anche, che AB = 0 significa che i due punti A e B
sono ōcoincidentiö, cioĶ in pratica sono lo stesso punto.
Per definizione, due bipunti si dicono uguali
(α = β) se per qualunque bipunto ξ si ha: α
ξ = β ξ .
Se ne deduce che condizione necessaria e
sufficiente perchķ due bipunti siano uguali Ķ che giacciano sulla stessa retta
e che le loro lunghezze orientate siano uguali.
Quindi AB
= AC significherÓ che B e C sono coincidenti.
Due punti sono uguali solo se essi
coincidono.
Ne segue che, per due punti materiali ![]() e
e ![]() , scrivere
, scrivere ![]() Ā, significherÓ che essi sono nello stesso
punto geometrico ed hanno la stessa massa. Mentre, se con gli stessi due
simboli indichiamo due sistemi meccanici con pi∙ punti materiali, lÆuguaglianza
tra i simboli significherÓ che i due sistemi hanno lo stesso baricentro e la
stessa massa totale; in particolare, se il sistema si muove (il movimento si
deve intendere solo come movimento relativo tra i punti del sistema, non avendo
alcun significato il movimento rispetto ad uno spazio assoluto in quiete
assoluta, chķ non abbiamo alcun modo di verificare),15 allora il ōsistema meccanicoö, per come formalmente
definito, resta uguale a se stesso, indipendentemente dalla posizione relativa
dei singoli punti durante il moto.
Ā, significherÓ che essi sono nello stesso
punto geometrico ed hanno la stessa massa. Mentre, se con gli stessi due
simboli indichiamo due sistemi meccanici con pi∙ punti materiali, lÆuguaglianza
tra i simboli significherÓ che i due sistemi hanno lo stesso baricentro e la
stessa massa totale; in particolare, se il sistema si muove (il movimento si
deve intendere solo come movimento relativo tra i punti del sistema, non avendo
alcun significato il movimento rispetto ad uno spazio assoluto in quiete
assoluta, chķ non abbiamo alcun modo di verificare),15 allora il ōsistema meccanicoö, per come formalmente
definito, resta uguale a se stesso, indipendentemente dalla posizione relativa
dei singoli punti durante il moto.
Da quanto detto risulta che si pu“ sempre
dare un significato ad unÆespressione simbolica come la (**) della pagina
precedente:
1) Se i vi
sono punti geometrici e gli ai , sono i valori delle
masse che si immaginano in essi concentrate, allora v rappresenta il punto materiale corrispondente al baricentro del
sistema meccanico in cui si immagina conŁcentrata la massa totale del sistema.
Ma possiamo, anche, pensare che gli ai siano i valori delle
cariche elettriche che si immaginano concentrate nei punti vi ,
allora v pu“ rappresentare il
centro delle cariche. Ma notiamo che, in questo caso, la somma delle cariche
pu“ risultare nulla, in quanto le cariche possono essere sia positive che
negative; in tal caso, il centro delle cariche non pu“ essere individuato, e
tuttavia si pu“ dare un significato allÆente v anche in questo caso degenere. Quindi consideremo, in astratto,
lÆespressione (**) e, se i vi
sono dei punti geometrici, allora diremo che v Ķ una ōformazione geometrica
di primo gradoö.
2) Se i vi
sono dei bipunti, dal punto di vista geometrico (cioĶ, se si considerano solo
le grandezze geometriche: angoli, lunghezze, aree e voluŁmi), v rappresenterÓ la somma di N segmenti
orientati che, generalmente, Ķ un segmento orientato. Ma, anche qui, si pu“
avere una degenerazione, noŁnostante la quale, si riesce tuttavia a dare un
significato geometrico (o anche fisico a seconda del significato degli ai)
allÆente v. In astratto: se i vi sono dei bipunti, allora
diremo che v Ķ una ōformazione
geometrica di secondo gradoö.
3) Se i vi
sono dei tripunti, a meno della solita possibile degenerazione, allora v rappresenterÓ unÆarea orientata (o, a
seconda del significato degli ai , qualche altra grandezza
fisica dipendente linearmente dallÆarea) e, poŁichķ anche in questo caso si pu“
dare significato alla situazione degenere, in astratto, parleremo di ōformazione
geometrica di terzo gradoö.
4) Se i vi
sono dei quadripunto, v sarÓ
sempre un volume, il caso degenere non ha alcun interesse, perchķ viene ad
essere semplicemente un volume nullo (ci“ dipende dal fatto che abbiamo assunto
che lo spazio fisico ha solo tre dimensioni, il risultato sarebbe diverso in
spazi astratti con pi∙ di tre dimensioni; spazi che spesso vengono considerati
in fisica). In astratto: se i vi
sono quadripunto diremo che v Ķ una ōformazione geometrica di quarto gradoö.
Riassumendo:
Due formazioni della stessa specie si possono
sommare per dare origine ad unÆaltra formazione della stessa specie (la specie
Ķ decisa dal significaŁto degli ai , la quale pu“ solo essere
decisa operativamente; la stessa specie implica lo stesso grado ma non
viceversa), ed esse si possono moltiplicare per un numero, restando della
stessa specie e quindi anche dello stesso grado.
Quindi se S ed S ′ sono formazioni della stessa specie e
se a e b sono numeri si ha:
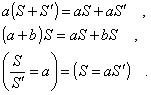
Due formazioni di qualunque grado possono
moltiplicarsi fra loro (terŁmine a termine) di modo che se S e T sono, rispettivamente, di grado s
e t (naturalmente s + t
ŻĀ 4) si otterrÓ una formazione
di grado s + t .
Possiamo considerare i numeri reali come
formazioni di grado zero, cioĶ rapporti di grandezze della stessa specie.
Se R,
S, T sono formazioni di specie opportuna si ha:
R (S+T) = RS + RTĀ
,
(S+T) R = SR + TR Ā,
R (ST) = (RS) T = RSTĀ
,
e, se a Ķ un numero:
(aR) SĀ = R (aS)Ā =Ā aRSĀ
.
Se R =
S e R ′= S ′ ,
allora si avrÓ:ĀĀ R R ′= S S ′
.
Nel seguito chiameremo ōmassaö, la somma
dei coefficienti delle formaŁzioni di primo grado, indipendentemente dal
significato fisico dei coefficienti numerici della formazione; questo ci Ķ
permesso per il fatto che, nello svilupŁpare il calcolo algebrico che abbiamo
istituito, ci occuperemo solo di relazioni puramente formali.
Ai nostri fini, enunceremo solo alcuni
teoremi, naturalmente senza le dimostrazioni, che sono date nella citata opera
di Peano.
ōSe A e B sono
punti, e a, b sono numeri, tali che a+b ╣ 0, allora esiste sempre un ōunicoö punto C tale
che (a + b)C = aA + bRö.
Se, in particolare, a e b
sono masse, C Ķ il baricentro del
sistema costituito dai due punti materiali aA e bB.
Come corollario, si ha che se tre punti A, B, C sono allineati, allora si
possono sempre trovare due numeri, a, b, tali
che (a + b)C = aA + bB.
Per cui possiamo enunciare il seguente
inportante teorema:
ōQualunque
formazione di primo grado di massa non nulla si pu“ sempre ridurre, in un modo
solo, a un punto solo (baricentro) moltiplicato per un coefficiente numerico
(massa)ö.
Ma vediamo che succede se la ōmassaö Ķ nulla
(caso ovvio quando, con il termine generico ōmassaö, vorremo intendere ōcarica
elettricaö o ōmassa magneticaö).
Sia ![]() Āuna formazione di primo grado e sia
Āuna formazione di primo grado e sia ![]() ; preso ad arbitrio un punto Q, possiamo sempre scrivere:
; preso ad arbitrio un punto Q, possiamo sempre scrivere:
![]()
Ma la formazione entro parentesi ha massa 1 e
quindi per il teorema precedente Ķ riducibile ad un punto P con coefficiente unitario.
Quindi ![]() .
.
Chiameremo ōvettoreö la differenza di
due punti.
Si pu“ dire che una formazione di primo grado
degenera nel punto alŁlÆinfinito (cioĶ nel punto improprio); pi∙ precisamente,
in una direzione, un verso e una lunghezza.
Un altro possibile significato geometrico per
una generica formazione di primo grado Ķ quello di una stella di rette nello
spazio; rette passanti per un punto (in effetti si tratta di segmenti
orientati, obbligati a scorrere sulle rette della stella; ma, in geometria
proiettiva, si fa astrazione dalle lunghezze, come anche dalle aree e dai
volumi). Tale stella degenera in un fascio di rette parallele (punto
allÆinfinito) quando la ōmassaö tende a zero.
Quindi:
ōUna
formazione di primo grado con massa nulla Ķ sempre riducibile, in un sol modo,
a un vettoreö.
E quindi:
ōUna
formazione di primo grado Ķ sempre riducibile a un punto con massa o a un
vettoreö (la
disgiunzione si deve intendere esclusiva).
╚ importante notare la differenza tra un vettore,
il quale Ķ una formaŁzione di primo grado, e un bipunto che, invece, Ķ una
formazione di secondo grado: il primo Ķ caratterizzato da una lunghezza, una
direzione e un verso; il secondo Ķ caratterizzato da una lunghezza, una retta e
un verso.
Due vettori paralleli con la stessa lunghezza
e con lo stesso verso sono lo stesso vettore, non cosņ per due bipunti che,
invece, saranno lo stesso bipunto solo se stanno sulla stessa retta (tuttavia,
lÆuguaglianza si ha indipendenteŁmente dalla loro specifica posizione sulla
retta).
Se a, b, c, u
sono quattro vettori dello spazio, Ķ sempre possibile trovare tre numeri p, q, r
tali che si possa scrivere:
u = pa + qb + rcĀ .
Se S Ķ un punto la cui distanza da PQR Ķ uguale allÆunitÓ di misura, che Ķ
stata stabilita per le lunghezze, allora il rapporto
APQRĀĀ
SPQR
rappresenta la distanza del punto A
dal piano di PQR,
presa col segno + o col segno -, a seconda che A ed S stiano dalla stessa parte
o da parti opposte rispetto al piano di PQR.
***
Se AB Ķ
un bipunto, diremo ōvettore di AB ö,
il vettore B - A.
Per definizione, porremo:
| B - A | = | AB |Ā .
Ogni bipunto si pu“ sempre considerare come
il prodotto Aa di un punto A
per il suo vettore a. Infatti basterÓ porre B = A + a e si
avrÓ:
AB = AaĀ .
Ogni bipunto si pu“ sempre considerare come
la somma di pi∙ bipunti con coefficienti unitari.
Con il calcolo geometrico su esposto si pu“
risolvere qualunque probleŁma di fisica o di geometria in forma simbolica
assoluta, cioĶ senza bisogno di menzionare le coordinate; come, al contrario, Ķ
necessario fare in geometria analitica. Anche se, quando si vuole, si possono
sempre introdurre esplicitamente le coordinate.
Ma enunciamo altri importanti teoremi.
ōQualsiasi
bipunto si pu“ trasformare in un altro bipunto avente per origine un punto
arbitrario della retta del primo e per vettore quello del bipunto datoö.
ōLa somma di
pi∙ bipunti con la stessa origine Ķ un bipunto che ha la stessa origine ed il
cui vettore Ķ la somma dei vettori dei bipunti datiö.
ōLa somma di
un qualsivoglia numero di bipunti, le cui rette passano per uno stesso punto, ķ
un bipunto passante per detto punto e che ha per vettore la somma dei vettori
dei bipunti datiö.
ōLa somma di
due bipunti paralleli, ma con la somma dei loro vettori non nulla, Ķ riducibile
a un bipunto parallelo ai primi due ed il suo vettore Ķ la somma dei vettori
dei due bipunti datiö.
In conclusione, raccogliendo tutti i
risultati precedenti:
ōQualsiasi
formazione di secondo grado, in un piano, con la somma dei loro vettori non
nulla, Ķ sempre riducibile a un solo bipunto il cui vettore Ķ la somma dei
vettori dei bipunti della formazione; se i bipunti della formazione sono tutti
paralleli, lÆorigine sarÓ il baricentro delle origini, avendo preso, come
masse, numeri proporzionali alle lunghezze dei vettori partecipanti alla somma;
se la somma dei vettori Ķ nulla, la formazione Ķ sempre riducibile alla somma
di due bipunti aventi vettori uguali e di segno contrario, uno dei due bipunti
si pu“ assegnare ad arbitrio nel piano (in meccanica si chiama coppia, qui la
chiameremo bivettore, perchķ si pu“ intendere sempre come il prodotto di
due vettori)ö.
Notiamo che un bivettore si pu“ anche
rappresentare come la somma dei tre bipunti che si possono individuare in un
dato tripunto e che tale somma non e il perimetro di quel triangolo che
corrisponde al tripunto ABC;
il perimetro Ķ infatti: | AB |
+ | BC | + | CA |Ā .
Diremo che un vettore a Ķ parallelo ad
un bivettore bc se i vettori a, b, c sono paralleli ad
uno stesso piano; cioĶ, se abc = 0.
Diremo che due bivettori ab e cd sono paralleli se a, b,
c, d sono paralleli ad uno stesso piano; cioĶ, se abcd =
0.
Tutto questo ci permette di dire che una
formazione di secondo grado, il cui vettore sia nullo, degenera in una retta
allÆinfinito o, che Ķ la stessa cosa: un fascio di piani attorno ad una retta,
degenera in un fascio di piani paralleli orientati e di data giacitura, che pu“
essere individuata da un vettore normale a detti piani.
Vale, naturalmente, lo stesso discorso che
abbiamo fatto nel caso dei vettori, cioĶ: anche se in geometria proiettiva non
sono definite lunghezze, areee e volumi, per cui siamo autorizzati ad usare il
linguaggio precedente, bisogna ricordare che il bivettore rappresenta lÆarea di
un triangolo con una giacitura ed un verso; la differenza con un tripunto Ķ che
questÆultimo Ķ obbligato a stare in un piano determinato, mentre due triangoli
con la stessa area, con lo stesso verso e con la stessa giacitura sono
rappresentati dallo stesso bivettore, quindi se spostiamo un triangolo
parallelamente a se stesso il bivettore corrispondente non muta, mentre il
tripunto corrispondente varia (tuttavia, il tripunto resterÓ immutato se il
triangolo si sposta sullo stesso piano).
Si pu“ enunciare la proposizione seguente:
ōLa somma di
quanti si vogliano bivettori nello spazio Ķ sempre riducibile ad un solo
bivettoreö.
Raccogliendo i risultati precedenti possiamo
affermare:
ōUna
formazione di secondo grado nello spazio Ķ sempre riducibile ad un bipunto
avente origine in un punto arbitrariamente scelto ma con vettore (che potrebbe,
eventualmente, anche essere nullo) che Ķ la somma dei vettori della formazione,
pi∙ un bivettore (che potrebbe, eventualmente, anche essere nullo)ö.
CioĶ, se ![]() ĀĶ una formazione di
secondo grado allora pu“ sempre porsi:
ĀĶ una formazione di
secondo grado allora pu“ sempre porsi:
![]() Ā,
Ā,
dove α Ķ un bipunto e A un
bivettore.
Quindi:
ōUna
formazione di secondo grado Ķ sempre riducibile alla somma di due soli
bipuntiö.
In meccanica le forze sono rappresentate da
bipunti; allora, con questo nuovo significato concreto per gli astratti bipunti
(notiamo che stiamo usando gli aggettivi concreto e astratto con significato
relativo, come Ķ necessario nella scienza), le conclusioni precedenti possono
essere ritradotte:
ōUn qualsiasi
sistema di forze pu“ essere sostituito in infiniti modi con la somma di due
sole forze; si pu“ prendere ad arbitrio la retta dÆazione di una delle due
forze purchķ la somma dei momenti delle forze del sistema (cioĶ la somma delle coppie,
o momento totale delle forze), rispetto a
tale retta, non sia nulla e tale retta non sia parallela alla risultante delle
forzeö.
Abbiamo, cosņ, ritrovato il teorema centrale
della statica dei sistemi di punti materiali.
***
ōLa somma di
due tripunti di uguale grandezza e di segno opposto Ķ un trivettore, cioĶ il prodotto di tre
vettoriö.
ōLa somma di
pi∙ tripunti, se la somma dei loro bivettori Ķ diversa da zero, si riduce a un
solo tripunto; se invece Ķ zero, si riduce ad un trivettoreö.
Il prodotto di un punto per un trivettore dÓ
il volume di un tetraedro, indipendente dalla posizione del punto.
Analogamente ai casi precedenti, un
trivettore, in geometria proiettiva, pu“ rappresentare un piano allÆinfinito.
Avendo fissato il volume unitario u, indicheremo con Ω il suo
trivettore, e per qualunque punto dello spazio si avrÓ: O ΩĀ =Ā u.
La massa di una formazione di prima grado
sarÓ: ![]()
Quindi, se ![]() , significa che
, significa che ![]() ĀĶ un vettore.
ĀĶ un vettore.
Se ![]() , allora
, allora ![]() ĀĀĶ il baricentro di
ĀĀĶ il baricentro di ![]() .
.
Se ![]() Ķ una formazione di quarto grado, il suo trivettore sarÓ dato
da:
Ķ una formazione di quarto grado, il suo trivettore sarÓ dato
da: ![]() Ā.
Ā.
Si dimostra che, dati tre vettori arbitrari a,
b, c, tali che abc ╣ 0, allora ogni altro vettore
dello spazio si pu“ esprimere come una loro combinazione lineare:
v = xa + yb + zc .
E i tre numeri x, y, z si dicono le coordinate di v,
rispetto ad a, b, c.
Se i
tre vettori coincidono con lÆusuale terna ortogonale di versori i, j,
k, usualmente si pone ijk = 1.
In termini delle rispettive coordinate
rispetto alla generica terna a, b, c, per un bivettore si
ha:
v
v′ = (yz′ - y′z)bc + (zx′ -Ā z′x)ca + (x y′ - x′ y)ab ;
per cui, un qualunque bivettore si pu“ porre sotto la forma:
V =
αbc + βca + γab.
In termini delle rispettive coordinate il
prodotto di un vettore per un bivettore vale:
vV′ = (xα′ + yβ′ + z γ′)abc.
E un prodotto di tre vettori vale:
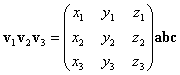 .
.
Siano i, j, k i tre vettori di riferimento (non
necessariamente ortogonali tra loro, nķ con la stessa lunghezza), costruiamo i
bivettori
I = jk ,
J = ki ,
K =
ij ,
siano:
v1 = x1i + y1j + z1k
,
v2 = x2i + y2j + z2k
,
V1 = X1I + Y1J + Z1K
,
V2 = X2I + Y2J + Z2K
,
allora si avra:
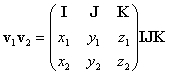 Ā;
Ā;
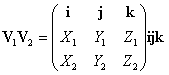 .
.
Se prendiamo i, j, k ortogonali tra loro e poniamo ijk
= IJK = 1, le due matrici esprimono (almeno per quanto riguarda i
numeri) lÆusuale prodotto vettoriale: v1 ┘ v2.
Ma vediamone il significato geometrico.
Definiamo un operatore ┴, tale che, operando su di
un bivettore, A,
produca un vettore, a, tale che la sua direzione sia ortogonale al
piano di A, il verso sia concorde al verso dellÆarea orientata stabilito
per A e con lunghezza uguale, in numero, allÆarea di A; lo
chiameremo, usando la terminologia di Hamilton e di Peano: lÆōindice di Aö.
Tranne che in particolari situazioni, useremo
la stessa lettera, scritta in minuscolo, per denotare lÆindice di un bivettore,
che invece scriveremo in maiuscolo:
a = ┴ A .
Notiamo che con tale definizione lÆusuale
prodotto vettoriale si pu“ scriŁvere:
a ┘ b =Ā ┴ ab .
LÆoperazione indicata da ┴ (che fa passare da bivettori
a vettori) Ķ biuniŁvoca e quindi possiamo introdurre lÆoperatore inverso che
indicheremo con T (che
fa passare da vettori a bivettori), cioĶ:
( a = ┴ A )Ā Ā=Ā ( A =Ā T a ) ;
e quindi:
T
┴ AĀ = A ;ĀĀĀĀĀ ┴ T aĀ = a .
Dalle definizioni segue:
( a = b ) = (
T a = T b ) ,
( A = B ) = (
┴ A = ┴ B ) ,
T
( a + b ) = ĀT a + T b ,
┴ ( ab ) = T a T bĀ ,
a T bĀ = b T aĀĀ ,
┴ ( aV + bW ) Ā=Ā a ┴ VĀĀ +ĀĀ b ┴ WĀ ,
T
V WĀ = ┴ V ┴ WĀ ,Ā
V ┴ WĀ
=Ā WĀ ┴ V Ā.
(La penultima equazione e da considerare,
qui, come una definizione nominale, dal momento che in uno spazio
tridimensionale non ha senso il prodotto di due bivettori. Tuttavia la formula
si dimostra come teorema dopo avere introdotto il ōprodotto regressivoö, o
ōintersezioneö, che qui non Ķ necessario introdurre).
Il prodotto scalare fra due vettori, lo
possiamo definire con:
a ū bĀ =Ā a T bĀ .
Una qualunque formazione di primo grado nello
spazio si pu“ sempre esprimere mediante le sue ōcoordinateö, rispetto a
un arbitrario sistema di riferimento, costituito da quattro arbitrarie
formazioni di primo grado tutte distinte tra loro:
Siano ![]() ,
, ![]() ,
, ![]() ,
, ![]() , le quattro formazioni di riferimento, con
, le quattro formazioni di riferimento, con ![]()
![]()
![]()
![]() Ā╣ 0, allora ogni formazione di primo grado,
Ā╣ 0, allora ogni formazione di primo grado, ![]() , pu“ scriversi mediante le coordinate x1, x2,
x3, x4:
, pu“ scriversi mediante le coordinate x1, x2,
x3, x4:
![]() Ā.
Ā.
Una qualunque formazione di secondo grado, ![]() , si pu“ esprimere meŁdiante sei coordinate:
, si pu“ esprimere meŁdiante sei coordinate:
![]() Ā.
Ā.
Una qualunque formazione di terzo grado, ![]() , si esprime mediante quatŁtro coordinate:
, si esprime mediante quatŁtro coordinate:
![]() Ā,
Ā,
avendo posto:
![]() =
= ![]()
Ā ![]() =
= ![]()
![]() =
= ![]()
ĀĀĀ ![]() =
= ![]() Ā.
Ā.
Le coordinate di una qualunque formazione si
possono sempre esprimere come rapporti di formazioni di quarto grado (cioĶ, di
volumi orientati di tetraedri):
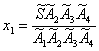 Ā, ecc.
Ā, ecc.
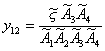 Ā, ecc.
Ā, ecc.
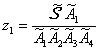 Ā, ecc.
Ā, ecc.
IlĀ prodotto
di quattro formazioni di primo grado, ![]() (i= 1,... ,4),
di coordinate, rispettivamente, xi, yi, zi,
ti, varrÓ:
(i= 1,... ,4),
di coordinate, rispettivamente, xi, yi, zi,
ti, varrÓ:
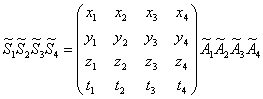 .
.
Poichķ le formazioni di primo grado possono
essere punti o vettori (in ogni caso un punto ōproiettivoö, proprio o improprio), abbiamo diverse
posŁsibili scelte per il sistema di riferimento. La scelta avverrÓ secondo la
coŁmoditÓ e lÆopportunitÓ del problema concreto in esame; ovviamente, sara
sempre possibile passare da un sistema di riferimento ad un altro mediante una ōtrasformazione
di coordinateö.
Diamo alcuni esempi usuali di sistemi di riferimento.
Se si scelgono quattro punti si avranno le
coordinate ōbaricentricheö.
Se scegliamo ![]() ,
, ![]() ,
, ![]() , Ā
, Ā![]() ,ĀĀ con i ū j = i ū k = j ū k = 0 e i2 =
j2Ā = k2Ā = 1, si otterranno le coordinate
cartesiane ortogonali ed ogni punto si potrÓ esprimere con:
,ĀĀ con i ū j = i ū k = j ū k = 0 e i2 =
j2Ā = k2Ā = 1, si otterranno le coordinate
cartesiane ortogonali ed ogni punto si potrÓ esprimere con:
P
= O + x i + y j
+ z k .
In questÆultimo sistema di coordinate, una
formazione di secondo grado si pu“ scrivere:
![]() .
.
Si ha:
![]() .
.
***
Le formazioni geometriche, come qualsiasi
altro ente, possono essere costanti o variabili in funzione di uno o pi∙ parametri,
come, p.es, il tempo o un punto o una qualsiasi altra formazione geometrica. Ad
esse, quindi, si possono facilmente estendere le nozioni di limite, derivata,
integrale, ecc.
Sia ![]() una formazione di primo grado di massa non nulla che vari con
continuitÓ in funzione del tempo t.
una formazione di primo grado di massa non nulla che vari con
continuitÓ in funzione del tempo t.
Consideriamo il rapporto incrementale:
![]() Ā.
Ā.
Se consideriamo il parametro t come una formazione di grado zero,
cioĶ un numero, allora tale rapporto sarÓ un vettore, venendo ad essere una forŁmazione
di primo grado di massa nulla (naturalmente, se ![]() fosse giÓ stato un vettore, sarebbe rimasto tale).
fosse giÓ stato un vettore, sarebbe rimasto tale).
Al limite, per t2 tendente
a t1, avremo la derivata della ![]() rispetto a t calcolata in t1; al
variare di t1, essa Ķ una nuova funzione del tempo,
che indicheremo con le usuali notazioni:
rispetto a t calcolata in t1; al
variare di t1, essa Ķ una nuova funzione del tempo,
che indicheremo con le usuali notazioni:
![]() .
.
DÆora in poi, non useremo pi∙
sistematicamente, come abbiamo fatto finora, il segno ̃, per distinguere le formazioni
geometriche dagli n-punti; la loro essenza risulterÓ chiara dal contesto.
In dinamica, la derivata di un punto
materiale si chiama ōquantitÓ di motoö; la quantitÓ di moto riferita allÆunitÓ di massa si chiama ōvelocitÓö (un ōpunto materialeö Ķ il prodotto di un ōpunto geometricoö per
una massa; quindi, nel descrivere a parole le varie situazioni, noteremo,
rispetto allÆuso tradizionale, una piccola differenza, la quale non pu“ portare
a confusioni se ci si attiene alle definizioni formali esplicitamente date,
come sempre si deve fare in qualsiasi teoria scientifica; allÆinterno del
calcolo sopra sviluppato, non si vede alcuna necessitÓ di separare il punto
geometrico dalla massa ad esso associata).
La derivata seconda si chiama ōforzaö; e la forza per unitÓ di massa si chiama ōaccelerazioneö.
Il bipunto A(t1 )A(t) rappresenta la corda istantanea che sottende lÆarco di curva
descritta dal punto A durante
lÆintervallo temporale compreso tra t1
e t (ōtraiettoriaö), chiameremo ōspostamentoö
tale bipunto (usualmente, con questo nome si chiama il vettore del bipunto,
cioĶ: A(t) - A(t1); noi useremo lo stesso nome per entrambi
i concetti, senza pericolo di ambiguitÓ, dal momento che la sua essenza
matematica viene chiaramente espressa dai simboli, i quali sempre risultano
molto pi∙ chiari del linguaggio comune, una volta compresone il significato; lo
stesso faremo per i termini prima introdotti, cioe: ōvelocitÓ, accelerazione,
quantitÓ di moto, forzaö).
Il tripunto A(t)A(t1 )A(t2) rappresenta un triangolo che varia nel
tempo. Al limite, per t1e t2
tendenti a t, otterremo il
tripunto: ![]() , il piano che lo contiene si chiama ōpiano osculatoreö;
ovviamente, esso varia al variare di t,
la sua giacitura Ķ quella del bivettore
, il piano che lo contiene si chiama ōpiano osculatoreö;
ovviamente, esso varia al variare di t,
la sua giacitura Ķ quella del bivettore ![]() .
.
Il piano del tripunto A T![]() si chiama ōpiano normaleö
e la sua giacitura, data dal bivettore T
si chiama ōpiano normaleö
e la sua giacitura, data dal bivettore T![]() ,
Ķ normale alla tangente alla curva, cioĶ alla velocitÓ.
,
Ķ normale alla tangente alla curva, cioĶ alla velocitÓ.
IlĀ vettore
(o, anche, la retta) del bipunto A ┴ ![]() Āsi dice ōbinormaleö.
Āsi dice ōbinormaleö.
LÆintegrale
![]()
rappresenta la lunghezza dellÆarco descritto dal punto, a partire dal
punto iniziale Ai ,
fino al punto finale Af ;
ovviamente, ![]() .
.
Invece, lÆintegrale
![]()
Ķ una formazione di secondo grado che rappresenta il limite verso cui
tende la somma dei tratti consecutivi della curva: AiA1 + A1A2 + . . . An Af ,
al crescere indefinito dei punti segnati sulla curva, in modo da far
tendere a zero la distanza tra due punti consecutivi. La lunghezza di tale
bipunto limite Ķ la lunghezza dello spostamento finale, a partire da quello
iniziale, cioe:
![]() Ā.
Ā.
Trasformazioni lineari
Le formazioni geometriche sono il paradigma
(nel senso antico del terŁmine) di un sistema lineare, per cui lÆalgebra delle
formazioni geometriche si pu“ estendere ad enti di specie pi∙ generale, purchķ
per essi si possano stabilire le stesse relazioni formali che abbiamo
individuato nelle formazioni geometriche.
Vediamo quali sono tali relazioni formali
ōelementariö (cioĶ quelle relaŁzioni, a partire dalle quali si possono dedurre
tutte le altre, cioĶ, le ōpropoŁsizioni primitiveö,
distinte in ōassiomiö e ōdefinizioniö;
le relazioni da esse dedotte sono chiamate da Peano ōproposizioni derivateö o ōteoreŁmiö; per“, tali
termini hanno, per lui, un valore soltanto relativo, in quanto spesso si
pu“ invertire il ruolo di alcune proposizioni primitive con quello di alcune
altre proposizioni derivate):
1) Si Ķ dato un significato determinato
allÆuguaglianza tra enti dello stesso sistema.
2) Si Ķ dato significato alla somma di enti
dello stesso sistema che produce un altro ente dello stesso sistema,
asserendone la commutativitÓ e lÆassociatiŁvitÓ.
3) Si Ķ dato significato alla moltiplicazione di un ente del sistema per un numero, asserendo che il risultato Ķ ancora un ente del sistema e che tale operazione Ķ commutativa.
4) Si Ķ dato significato allÆente ōnulloö
del sistema (che si pu“ indicare sempre con il simbolo ō0ö, senza pericolo di
ambiguitÓ, non potendosi mai confondere con lo zero dei numeri).
Un qualunque sistema di enti qualsiasi, con
le proprietÓ sopraelencate, lo chiameremo un ōsistema lineareö.
Ovviamente, sono sistemi lineari le formazioni
geometriche dello stesso grado (comprese quelle di grado zero, come i numeri).
Ma non sono sistemi lineari i punti, il segmento orientato tra due punti o
lÆarea orientata di un triangolo, in quanto una loro combinazione lineare
potrebbe dare un ente di natura diversa, come un ōmultivettoreö
(rispettivamente: un vettore, un bivettore o un trivettore). Tuttavia, i
multivettori dello stesso grado formano dei sottosistemi lineari, in quanto una
lora combinazione lineare Ķ ancora un multivettore dello stesso grado.
Se n enti
Ai di un sistema lineare
sono tali che si possano determinare n numeri,
ai, non tutti nulli, per cui si abbia:
![]() ,
,
tali enti si diranno ōlinearmente dipendentiö tra loro (in caso
contrario si diranno ōlinearmente indipendentiö).
Il numero massimo degli enti di un sistema
lineare, che si possono prenŁdere tutti indipendenti tra loro, si chiama il ōnumero
delle dimensioniö (o, pi∙ semplicemente, la ōdimensionalitÓö) del
sistema. Qualunque altro ente del sistema potrÓ essere rappresentato come una
combinazione lineare di n enti
indipendenti arbitrariamente scelti, che si chiamano una ōbaseö del
sistema:
![]() .
.
La dimensionalitÓ delle formazioni
geometriche di primo grado nello spaŁzio fisico Ķ 4, nel piano Ķ 3, sulla retta
Ķ 2, quella del sottosistema dei vettori Ķ 3 nello spazio, 2 nel piano, 1 sulla
retta.
Le formazioni geometriche di secondo grado
nello spazio formano un sistema lineare a 6 dimensioni, quelle di grado zero,
come i numeri, formano un sistema lineare di dimensionalitÓ 1, ecc.
Per altri tipi di sistemi lineari, la
dimensionalitÓ pu“ essere qualunque, a seconda del caso specifico, anche
infinita, come nel caso di un sistema lineare costituito da una classe chiusa
di funzioni (collÆaggettivo ōchiusoö intenderemo, in questo contesto, che una
combinazione lineare di enti della classe resta sempre un ente della stessa
classe), per la quale basterÓ intendere la somma di due funzioni come la somma
dei valori che esse assumono per un dato valore (del resto qualsiasi)
dellÆargomento, ecc., in particolare, il sistema dei polinomi di grado n di una variabile Ķ un sistema lineare
a n dimensioni.
Chiameremo ōoperatoreö, un qualsiasi
ente che applicato ad un ente del sistema produce un altro ente di un altro
sistema o, anche, dello stesso sistema.
Tutti i teoremi enunciati per le formazioni
geometriche, ovviamente, varranno anche per tutti i sistemi lineari, dal punto
di vista delle relazioni formali, indipendentemente dal loro significato fisico,
che pu“ essere il pi∙ vario; naturalmente, il sistema su cui agisce lÆoperatore
pu“ essere diverso dal sistema in cui Ķ definito il risultato dellÆoperazione;
p. es., lÆoperatore lineare ┴ agisce sui bivettori e dÓ per risultato un vettore,
il viceversa vale per lÆoperatore lineare T; cioĶ quello che per lÆuno Ķ il dominio, per
lÆaltro ne Ķ il codominio e viceversa.
Particolare attenzione meritano gli operatori
lineari, per la loro imporŁtanza nelle teorie fisiche, per cui enuncieremo
alcune proposizioni rilevanti su di essi, in forma astratta. La forma astratta,
appunto per il fatto che astrae dai possibili significati concreti degli enti
di cui tratta, per un verso, fa perdere il contatto con lÆintuizione fisica,
ma, per un altro verso, proprio per la precedente ragione, assume un grado di
generalitÓ tale che le sue relazioni formali restano valide in moltissimi casi
concreti, i pi∙ diversi tra loro.
Le teorie della fisica sono il miglior
veicolo per lÆassimilazione del proŁcesso dialettico tra astratto e concreto.
La confidenza con una sola di queste due forme di rappresentazione della
realtÓ, renderebbe questÆultima, cioĶ la realtÓ, assolutamente monca come un
corpo senza testa o una testa senza corpo.
DÆora in avanti, useremo le lettere maiuscole
per gli operatori lineari, le lettere minuscole in grassetto per gli enti di un
qualsiasi sistema e le lettere minuscole in corsivo per i numeri.
Un operatore lineare lo chiameremo, anche, ōtrasformazioneö; e, se dominio e codominio coincidono, lo diremo una ōsostituzioneö.
Dati due sistemi lineari A e B di uguale dimensionalitÓ n, e data una particolare
trasformazione, R,
che porta un ente a di A in
un ente b di B, scriveremo:
b = R
a.
Quando vorremo essere pi∙ espliciti
scriveremo:
[b ¼ a] = [b1, b2,
. . . , bn ¼ a1, a2, . . ., an]Ā ,
per dire che la trasformazione R =
[b ¼ a],
la intendiamo riferita ad una rappresentazione in cui si Ķ scelto un
sistema di n enti di AĀ : a1, . . . , an
indipendenti (ōbaseö) per rappresentare ogni ente di A; e una ōbaseö, b1,
b2, . . . , bn per rappresentare
ogni ente di B.
Che, ovviamente, significa:
R a1 = b1 ; . . . ; R an = bn
![]() .
.
In particolare, una coordinata di a,
nel dato riferimento (cioĶ nella data base), p. es. c1, si
potrÓ scrivere:
c1 = [1, 0, 0, ģ, 0 ¼ a1,
a2, . . ., an]a .
Se R =
[b ¼ a],
scriveremo per la trasformazione inversa: R -1 = [a ¼ b].
Se R Ķ
una ōsostituzioneö porremo, per definizione:
(1)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
Un elemento di un sistema lineare con una sola
dimensione si dice uno ōscalareö. Le formazioni geometriche di grado
zero sono quindi scalari.
Un elemento di un sistema di sostituzioni tra
vettori si dice un ōtensoŁreö. Oggi, si usa tale nome anche
per sostituzioni pi∙ generali.
Sia a un vettore fissato dello spazio
e sia x un vettore arbitrario. La relazione:
(2)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ s = Āa T x = a ū x
che dÓ la componente di x lungo la direzione di a, la
possiamo scrivere:
(3)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ s = ω1(
x )
interpretando ω1 =
a T = a ū
come una trasformazione con dominio i vettori dello spazio e codominio gli
scalari che rappresentano le loro componenti lungo a.
Viceversa, se si ha una qualunque
trasformazione lineare, ω1, che fa passare da vettori a scalari,
Ķ sempre possibile trovare un unico vettore a tale che si possa porre ω1 = a T = a ū .
Una qualunque funzione lineare definita sui
vettori, come la ω1, si
usa chiamare una ō1-formaö.
Per quanto detto sopra, Ķ chiaro che
lÆinsieme di tutte le 1-forme definite su un dato sistema di vettori si pu“
sempre considerare come un altro sistema di vettori (non necessariamente
identificabile con il primo) e quindi costituisce un altro sistema lineare con
la stessa dimensionalitÓ, che si dice il sistema ōdualeö
del primo.
Modernamente si usa, impropriamente, chiamare
vettore un qualsiasi sistema lineare, ed Ķ in questo senso generalizzato che
continueremo a usare il termine, adeguandoci allÆuso comune; avvertendo, per“,
che bisogna andare molto cauti nellÆadoperare il termine nelle applicazioni
concrete della fisica. Lo stesso varrÓ per i multivettori che ora possono avere
un grado qualsiasi, in dipendenza della dimensionalitÓ del sistema di vettori,
mediante i quali sono definiti.
Un esempio concreto di 1-forma Ķ il lavoro
elementare compiuto da una forza:
(4)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ dL = F ū dlĀĀ .
Consideriamo il trivettore,
nello spazio fisico,
(5)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ axy
= a T ┴ xyĀ = a ū (x ┘ y)ĀĀ ,
con a,
un vettore fissato, e, x e y, vettori arbitrari.
Dividendo per lÆunitÓ di misura stabilita per
la grandezza di axy, avremo una funzione scalare sĀ che dipende linearmente sia da x, sia da y,
(ōbilineŁareö) ed Ķ antisimmetrica rispetto a x e y, cioĶ:
(6)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ axy
= - ayxĀ .
La (5) si pu“ scrivere:
(7)ĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ s = ω2(
x, y )Ā ,
avendo indicato con ω2 quellÆoperatore che produce
lo scalare axy, dati due vettori qualsiasi, x e y.
Generalizzando: una qualunque funzione
bilineare e antisimmetrica si dice una ō2-formaö:
(8)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ω2(
a1 x1 + a2 x2 ,
y ) = a1
ω2(
x1, y )Ā + a2 ω2(
x2, y )Ā .
(9)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ω2(
x, y )Ā =Ā - ω2(
y, x )Ā
Un esempio di 2-forma Ķ lÆarea orientata di
un bivettore xy, che possiamo anche scrivere, in termini di coordinate:
(10)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ 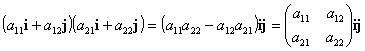 .
.
Nei casi, in cui fisicamente abbia senso la
somma tra possibili ω2, definite su di un dato
sistema lineare, e si possa scrivere:
(11)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() Ā ,
Ā ,
allora tale insieme di 2-forme sarÓ anchÆesso un sistema lineare a
(12)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]()
dimensioni.
Si generalizzano i concetti precedenti e si
definiscono le k-forme come: quelle funzioni multilineari di k
vettori, totalmente antisimmetriche, cioĶ tali che scambiando di posto, tra
loro, due qualsiasi dei k vettori, la
forma cambia di segno, se la permutazione Ķ dispari, o resta dello stesso
segno, se la permutazione Ķ pari (cioĶ, si comporta come un multivettore).
Definendo le combinazioni lineari di k-forme,
si viene a formare un sisteŁma lineare di dimensionalitÓ ![]() Ā,
essendo n la dimensionalitÓ
dei vettori su cui la k-forma Ķ definita.
Ā,
essendo n la dimensionalitÓ
dei vettori su cui la k-forma Ķ definita.
Quindi, a parte la differenza di
nomenclatura, formalmente (cioĶ, indiŁpendentemente dal loro significato
concreto, da stabilire in ogni singola siŁtuazione) le k-forme sono la
generalizzazione delle formazioni geometriche a spazi di qualunque
dimensionalitÓ, e gli elementi di tali spazi, impropriamenŁte chiamati vettori,
sono sempre interpretabili come particolari trasformaŁzioni.
Infatti, qualsiasi k-forma, in uno spazio
a n-dimensioni, si pu“ sempre esprimere, in un sol modo, come una
combinazione lineare delle forme di base:
(13)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]()
BasterÓ porre:
(14)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
essendo gli ej, i vettori della base.
Il concetto di campo
In fisica il concetto di campo Ķ
frequentemente usato nei pi∙ svariati contesti e spesso, perci“, dal punto di
vista epistemologico, sono stati espressi seri dubbi sulla sua effettiva
interpretazione fisica in determinate applicazioni concrete, come, p. es.,
nella teoria elettromagnetica.
Dal punto di vista astratto, cioĶ puramente
formale, invece, la nozione di campo Ķ molto semplice.
Diremo ōcampoö una qualunque porzione di
spazio fisico in ogni punto P del
quale Ķ definita univocamente una determinata grandezza fisica G:
G = G(P)Ā .
Se G Ķ uno scalare, lo diremo un ōcampo
scalareö; se un vettore, un ōcampo
vettorialeö; se un tensore,
un ōcampo tensorialeö.
Se G Ķ variabile nel tempo, parleremo
di ōcampo variabileö:
G = G(P,t)Ā .
Ma, ovviamente, dal punto di vista astratto,
si pu“ generalizzare il conŁcetto e chiamare campo un qualsiasi elemento G,
di un sistema lineare quŁalunque, funzione degli elementi P di un altro sistema lineare qualunque; non si pretende che la
funzione che lega G a P sia
lineare; ma, spesso, si pretende che G sia
funzione continua di P e derivabile a
qualsiasi ordine (ma nemmeŁno queste sono condizioni necessarie per un sistema
fisico, usualmente, esse vengono imposte per rendere pi∙ semplice la
trattazione matematica).
Facciamo alcuni esempi di applicazione del
concetto di campo nella fisica, dove alla stessa struttura matematica (e,
spesso, anche per spiegare lo stesso fenomeno, a causa di diversi paradigmi
filosofici) vengono attribuiti significati del tutto diversi.
Prendiamo, ad esempio, un corpo e
consideriamone, idealmente, una sua porzione qualsiasi, anche interna al corpo
stesso e sia DV il
volume dello spazio occupato da tale porzione e sia D m la
sua massa.
Si definisca la densitÓ media di tale porzione
con il rapporto:
(15)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
Sia P un
punto dello spazio (considerato come elemento di una formaŁzione geometrica di
primo grado), interno a tale porzione del corpo e imŁmaginiamo di prendere
porzioni sempre pi∙ piccole del corpo, che comunque contengano sempre il punto P al suo interno. Se immaginiamo la
materia coŁme distribuita continuamente allÆinterno del corpo, al limite per DV tendente a zero potremo
scrivere:
(16)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
Se, invece, pensiamo che la materia sia
discontinua, cioĶ fatta di partiŁcelle elementari inframmezzate da spazio
vuoto, allora non ha molto senso la nozione di derivata, nella pi∙ usuale
definizione, (naturalmente, se ne pu“ geŁneralizzare il concetto fino a
comprendere anche situazioni totalmente disconŁtinue come questa) ma, per il
momento, ci accontenteremo di unÆapprossiŁmazione, quasi sempre ottima nelle
applicazioni pratiche, che ci permette di utilizzare lÆusuale calcolo
differenziale e integrale.
CioĶ, si immagina di avere un DV, che
sia sufficientemente piccolo da consentire di poter trascurare infinitesimi di
ordine superiore nello sviluppo in serie della densitÓ, in funzione di uno
spostamento allÆinterno di DV; e, nello stesso tempo,
sufficientemente grande da contenere un numero enorme di particelle elementari,
in modo che si possano trascurare le fiuttuazioni staŁtistiche, e cosņ
ottenere, per la densitÓ, una funzione ρ(P),
sufficientemente regolare che possa rappresentare la situazione reale con
buona approssimaŁzione.
Questo genere di approssimazione Ķ la norma
nelle applicazioni fisiche della matematica, ma spesso in fisica ci si
dimentica che qualcosa che Ķ sotŁtintesa non Ķ per niente scomparsa!
Tale distribuzione di densitÓ, ovviamente,
corrisponde ad un campo scaŁlare.
Il valore della densitÓ in un punto P potrebbe variare anche nel tempo,
avremo un campo scalare variabile:
ρ = ρ(P,t) ;
lÆesempio classico Ķ quello di un fluido in movimento.
Supponiamo di essere in una tale situazione, che
con buona approssimaŁzione Ķ realizzata da una corrente dÆacqua di portata
costante che si muova con velocitÓ non molto elevata in una condotta che
possiamo pensare fatta di vetro in modo da vedere cosa accade alla corrente;
anzi, a tale scopo, immaginiamo di immettere in un punto qualunque della
corrente, con opportuni imbutini, un filetto di acqua colorata (p. es.,
inchiostro), o un granello di permanganato potassico che sciogliendosi
rapidamente genera dei filetti fluidi colorati facilmente visibili anche ad
occhio nudo.
Finchķ tali filetti non si saranno dispersi,
possiamo osservare quelle che si chiamano le ōlinee di correnteö
o ōlinee di flussoö; un gruppo compatto di tali linee ci dÓ lÆidea di
quello che in effetti si chiama un ōtubo di flussoö, che Ķ lÆinsieme di
tutte linee di flusso che attraversano ogni punto di una qualunque sezione
ideale che tagli la corrente.
In un fluido stazionario tali linee restano
sempre identiche col passare del tempo. La velocitÓ con la quale si propaga il
filetto colorato si suppone essere la stessa con la quale si muove ogni
elemento del fluido. Essa Ķ definita in ogni punto del fluido da un vettore v
che varia da punto a punto ma che, nel caso stazionario, resta sempre lo stesso
nello stesso punto del fluido.
Questo Ķ un esempio di ōcampo vettorialeö:
vĀ =Ā v(P)Ā .
Il vettore v Ķ in ogni punto tangente
alla linea di flusso passante per quel punto.
Nel caso non stazionario sarÓ anche funzione
del tempo:
v = v(P,t)Ā
.
Consideriamo ora una porzione elementare di
volume di un solido elastiŁco e immaginiamo di sottoporlo ad uno sforzo di
tensione o di pressione, esso si allungherÓ o si accorcerÓ per effetto dello
sforzo. Per semplicitÓ, suppoŁniamo che lÆelemento di volume che stiamo
considerando abbia forma cubica e prendiamo un sistema di riferimento con
origine in uno dei vertici del cubo e con assi coordinati lungo gli spigoli che
si dipartono da tale vertice.
Supponiamo di applicare uno sforzo
allÆelemento di volume consideraŁto, sia dfx
la sua componente lungo la direzione x e che, quindi, si esercita
normalmente alle due facce parallele al piano yz; e, analogamente, definiamo le
componenti dfy,
e dfz (si Ķ soliti
considerare la forza allÆunitÓ di superfice normale in un intorno del punto
considerato). Siano dx,
dy, dz gli allungaŁmenti (positivi o negativi) che subisce lÆelemento
di volume per effetto dello sforzo complessivo: df = dfxi + dfyj + dfzk
.
In generale si ha:
dx =
a11dfx + a12dfy + a13dfz
dy =
a21dfx + a22dfy + a23dfz
dz =
a31dfx + a32dfy + a33dfz
Dove gli aij
sono dei coefficienti che possono essere funzioni del punto intorno al
quale abbiamo scelto lÆelemento infinitesimo di volume ed, evenŁtualmente,
anche del tempo, ma non dipendono dallÆintensitÓ dello sforzo applicato o,
meglio, dalle variazioni degli sforzi, dfx
, dfy , dfz , (proprio meŁdiante
tali condizioni viene data la definizione stessa di solido elastico; in realtÓ
si possono avere delle piccole non linearitÓ per sforzi relativamente grandi).
Per ragioni fisiche, tali nove coefficienti non sono tutti indipendenti tra
loro, ma qui la cosa Ķ per noi irrilevante.
Le tre relazioni, che abbiamo scritto sopra,
le possiamo anche scrivere in forma vettoriale, ponendo dl = dxi + dyj + dzkĀ :
(17)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ dl
= A dfĀ ,
doveĀ A Ķ una trasformazione
lineare da vettori a vettori e, quindi un tensore.
Questo Ķ un esempio di campo tensoriale, anzi il nome tensore deriva dalle tensioni interne con le quali il solido reagisce agli sforzi esterni per equilibrarli e che si ipotizza siano causate dalle forze intermolecolari.
Occupiamoci, ora, pi∙ particolarmente, dei
campi vettoriali, i quali sono di grande rilevanza per lo studio
dellÆelettromagnetismo.
Qui avremo a che fare con un concetto di
campo che, pur avendo sempre la stessa definizione formale, invece, dal punto
di vista della fisica, risulta concettualmente diverso dallÆidea che ci siamo
andati formando attraverso gli esempi concreti di natura idrodinamica che
abbiamo dato finora.
Consideriamo una carica elettrica (ma lo
stesso discorso si pu“ ripeŁtere, senza rilevanti modifiche, per una massa
magnetica o per una massa gravitazionale).
Supponiamola fissa in un certo punto O di un dato riferimento.
Se si pone unÆaltra carica elettrica in un
punto P, a una certa distanza dalla
prima, fra le due si esercita una forza data dalla:
(18)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ;
;
per una data variazione della carica q si ha:
(19)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀ dF = EdqĀ ,
con
(20)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]()
Quindi il vettore E, definito su tutti
i punti P dello spazio, dal punto di
vista formale, costituisce un campo vettoriale, chiamato appunto ōcampo elettrostaticoö.
Ma cÆĶ una sostanziale differenza, dal punto
di vista fisico, con il campo delle velocitÓ che Ķ definito nei punti di un
fluido; non perchķ si tratta di due grandezze fisiche diverse, chķ questo
sarebbe irrilevante in questo contesto, ma perchķ, nel caso del fluido,
lÆesistenza del campo in un punto del fluido stesso Ķ sempre definito, in
quanto il campo Ķ creato dal movimento della materia fluida, la quale, a sua
volta, costituisce il campo scalare a partire dal quale Ķ definito il campo
delle velocitÓ; mentre, nel caso di un campo di forza con interazione a
distanza, la forza sarÓ effettivamente agente solo in presenza di una carica di
prova, e solo in questo caso potrÓ avere senso parlare di campo di forza in un
punto, essendo questo zero in tutti gli altri punti dello spazio; e, dÆaltra
parte, la presenza della stessa carica di prova verrebbe, indirettamente, a
modificare profondamente il campo delle forze che agisce sul punto P, per effetto dellÆinfluenza che essa
esercita sulle cariche che creano il campo.
Naturalmente la quantitÓ matematica Ķ perfettamente definita e nienŁte ci impedisce di usarla coerentemente nella teoria per determinare altre grandezze fisiche misurabili, solo non possiamo, a partire dalla sua definiŁzione formale, misurare direttamente un campo perchķ, operativamente, noi possiamo misurare solo forze; anche se, nel caso che la carica di prova sia sufficientemente piccola da non provocare variazioni sensibili, si potrebbe effettuare una verifica diretta.
Per quanto detto, le formule saranno le
stesse sia che vengano interpreŁtate secondo il modello idrodinamico, sia che
lo siano secondo il modello delle forze agenti a distanza, ma il loro
significato fisico potrebbe risultare profonŁdamente diverso e potrebbe
condurre a rilevanti errori interpretativi, se non si fa attenzione alla
sostanziale differenza concettuale che abbiamo messo in luce. Tali errori non
sono infrequenti nelle moderne speculazioni teoriche.
Quello che abbiamo detto risulta molto pi∙
rilevante nel caso dei campi elettrici e magnetici, di quanto non sia per i
campi gravitazionali, a causa del fenomeno di induzione, dal momento che non Ķ,
in generale, trascurabile il campo creato dalle cariche di induzione che si
vengono ad aggiungere alla carica originale Q
che crea il campo.
Perci“ appare assolutamente illusoria, come
osservava Boltzmann, la credenza che si possa costruire una teoria fisica a
partire dalle leggi empiriche.
Si usa chiamare ōintensitÓ del campoö, il vettore del campo.
Se la carica Q, che crea il campo, Ķ in movimento, allora il campo sarÓ, in
generale, dipendente dal tempo.
Sono importanti per il seguito gli operatori
differenziali introdotti da Hamilton.
Intanto introduciamo il concetto di ōdifferenzialeö
nella forma generaŁlizzata, usata dal Peano, valida per enti lineari qualsiasi:
Sia x un ente di un qualsiasi sistema
lineare S, e sia y = f(x),
una sua funzione, il cui risultato y sia un ente di un altro
qualsiasi sistema lineare R.
Se x′ Ķ un ente qualsiasi di S,
poniamo, per definizione:
(21)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
LÆente ![]() , ovviamente, appartiene al sistema R ed Ķ funzione di x e di x′
e, nellÆipotesi che il limite indicato nella (21) esista, si chiama ōdifferenziale
della funzione f(x) calcolato in xö.
, ovviamente, appartiene al sistema R ed Ķ funzione di x e di x′
e, nellÆipotesi che il limite indicato nella (21) esista, si chiama ōdifferenziale
della funzione f(x) calcolato in xö.
LÆente x′ si dice ōdifferenziale della variabile indipendente
xö.
Se x e x′ sono ben
determinati, scriveremo semplicemente: df .
Facciamo degli esempi semplici:
Supponiamo che S ed R siano entrambi campi scalari funzioni
di un parametro t,
si avra:
(22)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
(23)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ĀĀ .
ĀĀ .
Sia S un sistema lineare ad m dimensioni con i vettori di base (e1,...
,em), ed R un sistema lineare ad n dimensioni con i vettori di base (b1,...
,bn) e sia y = f (x).
Si abbia:
xĀ = x1e1 + ... + xmem
(24)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ x′
= x′1e1 + ... + x′mem
ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ yĀ = y1b1 +
... + ynbn
si avra:
(25)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ 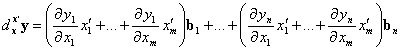 .
.
Oggi Ķ pi∙ comune la seguente scrittura:
(26)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
NellÆoperazione precedente ![]() ĀĶ un operatore
lineare sul sistema S:
ĀĶ un operatore
lineare sul sistema S:
(27)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
In termini di coordinate, Ķ rappresentato da
una matrice rettangolare n ┤ m.
Se n = m,
il suo determinante, indicato con:
(28)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ J
![]() ĀĀ,
ĀĀ,
si usa chiamare ōjacobianoö.
Sia f(P)
una funzione scalare del punto P di
uno spazio astratto a n dimensioni,
sia u un vettore differenza di due punti di detto spazio; essendo ![]() operatore lineare, esisterÓ sempre, per quanto detto sui
sistemi lineari, un vettore nello spazio duale,16 che qui indicheremo con a(P),
eventualmente dipendente da P,
ma non da u, tale che si possa porre:
operatore lineare, esisterÓ sempre, per quanto detto sui
sistemi lineari, un vettore nello spazio duale,16 che qui indicheremo con a(P),
eventualmente dipendente da P,
ma non da u, tale che si possa porre:
(29)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() a T u = a ū uĀ .
a T u = a ū uĀ .
Il vettore a si dice il ōgradienteö
di f calcolato in P (nella letteratura pi∙ antica veniva
chiamato, ōparametro differenzialeö), spesso si indica, seguendo
Hamilton, con č:
(30)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
dove si Ķ posto: r = P - O, essendo O un punto arbitrario.
Notiamo che lÆoperazione ![]() Āa ū = a T Ķ un operatore lineare sui vettori u,
e non un vettore, mentre č Ķ un operatore lineare
sulle funzioni scalari di punto, che le trasforma in vettori, quindi Ķ un ōoperatore
vetŁtorialeö, nel senso che si pu“ immaginare come la somma di tre
derivazioni lungo tre direzioni indipendenti, per cui si ha:
Āa ū = a T Ķ un operatore lineare sui vettori u,
e non un vettore, mentre č Ķ un operatore lineare
sulle funzioni scalari di punto, che le trasforma in vettori, quindi Ķ un ōoperatore
vetŁtorialeö, nel senso che si pu“ immaginare come la somma di tre
derivazioni lungo tre direzioni indipendenti, per cui si ha:
(31)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ č (fg) = fĀ č gĀ + g č fĀ .
A voler essere coerenti, si dovrebbe scrivere
(32)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() = č fĀ T = č fĀ ūĀĀ ;
= č fĀ T = č fĀ ūĀĀ ;
ma lÆidentificazione tra due oggetti algebricamente diversi, che
tuttavia si riferiscono biunivocamente allo stesso concetto geometrico o fisico,
non neŁcessariamente porta a inconvenienti semantici; purchķ si tenga sempre
ben presente la loro diversitÓ formale, nelle manipolazioni algebriche; le
quali, fatte meccanicamente, potrebbero portare a incongruenze, con ovvie conseŁguenze
anche sul piano semantico.
Se fissiamo un sistema di coordinate
cartesiane ortogonali, con origine O,
e poniamo r = P - O, si pu“ scrivere:
(33)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
come si verifica facilmente, essendo ![]() Āun operatore lineare
sul sistema lineare delle funzioni scalari; tuttavia, ricordiamo che il
gradiente Ķ un ente assoluto, cioe indipendente dal sistema di coordinate
scelto, perci“ si Ķ soliti dire che e invariante per arbitrarie trasformazioni
di coordinate.
Āun operatore lineare
sul sistema lineare delle funzioni scalari; tuttavia, ricordiamo che il
gradiente Ķ un ente assoluto, cioe indipendente dal sistema di coordinate
scelto, perci“ si Ķ soliti dire che e invariante per arbitrarie trasformazioni
di coordinate.
Naturalmente, il gradiente pu“ esistere solo
se la funzione scalare Ķ deŁrivabile nel punto considerato e in qualsiasi
direzione.
Per un circuito chiuso si ha:
(34)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
Viceversa, se in una campo vettorialeĀ v (r) , per
qualunque circuito si ha:
(35)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
allora, necessariamente, esiste una funzione scalare j (r),
definita a meno di una costante arbitraria, che si dice ōpotenzialeö e
tale che si abbia:
(36)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
Un particolare sviluppo in serie per un campo
scalare, in termini delŁlÆoperatoreč deriva dal fatto che
lÆoperatore ![]() gode di tutte le proprietÓ delle derivate rispetto a una
variabile numerica, e quindi possiamo sviluppare in serie di Taylor una
funzione scalare e scrivere:
gode di tutte le proprietÓ delle derivate rispetto a una
variabile numerica, e quindi possiamo sviluppare in serie di Taylor una
funzione scalare e scrivere:
(37)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ 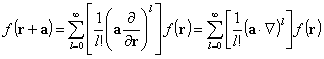 ;
;
che, per la (1), con la quale abbiamo definito lÆoperatore
esponenziale, posŁsiamo scrivere:
(38)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
In un campo vettoriale arbitrario, v (r),
consideriamo lÆintegrale lungo una linea chiusa, l, supponendo che
sia ben definito il valore di tale integrale di linea:
(39)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
essendo dl un vettore tangente alla linea nel punto P = O
+ r e O unÆorigine arbitraria; la quantitÓ C si chiama la ōcircuitazioneö del campo vettoriale v lungo la
linea chiusa l.
Il valore di dC per un circuito chiuso elementare (preso intorno ad un punto P = O + r) che tuttavia indicheremo
semplicemente con dl, Ķ:
(40)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
ed Ķ una funzione scalare di campo.
***
Sia v (P) un arbitrario campo vettoriale.
Si chiama ōflussoö elementare del
vettore v in un punto P dello
spazio, il trivettore:
(41)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ dF = dS
v T n = v(P) ū dSĀĀ ,
essendo n un versore normale allÆelemento di superficie dS (con verso dato dalla solita regola
di orientazione) e avendo posto per definizione dS =
n dS .
Quindi possiamo anche scrivere:
(42)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ dF = v ū dS
= | v | | dS
| cosq =
vn | dS | = | v | dSn Ā,
essendo q, lÆangolo tra le direzioni
di v e dS, vnĀ la componente normale alla
superficie dS e dSnĀ lÆelemento di superficie normale
al campo.
Per una superficie arbitraria S, il
flusso del campo attraverso di essa, Ķ:
(43)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() Ā .
Ā .
Se v Ķ il vettore velocitÓ di campo,
in un punto di un fluido, per una superficie elementare si ha:
(44)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() Ā ;
Ā ;
quindi, esso rappresenta, in questo caso concreto, la ōportataö, cioĶ, il voŁlume di fluido che attraversa la
superficie dS, nellÆunitÓ di tempo.
Per una superficie chiusa si conviene di assegnare il segno positivo a un flusso uscente e negativo al flusso entrante.
Se allÆinterno di una superficie chiusa S
non si hanno ōsorgentiö o ōpozziö per il flusso o se lÆintensitÓ
che esce dalle sorgenti Ķ pari allÆintensitÓ assorbita dai pozzi, allora il
flusso totale uscente da quel volume (consideŁrato algebricamente) deve essere
nullo perchķ il volume del fluido entrante Ķ sempre uguale e opposto a quello
uscente. Tale terminologia idrodinamica viene usata anche nelle altre
interpretazioni del campo vettoriale, anche in quei casi in cui non Ķ possibile
immaginare alcun fluido che scorra.
Se il flusso totale uscente Ķ diverso da
zero, allora necessariamente deŁvono esistere delle sorgenti positive o
negative (pozzi) in qualche punto o in tutti i punti del dato volume, tali che
la loro somma algebrica non sia nulla (useremo nel seguito il termine
ōsorgenteö, anche per i pozzi, il segno dellÆintensitÓ di sorgente ci dirÓ se
si tratta dellÆun caso o dellÆaltro).
Si chiama ōdivergenzaö del campo
vettoriale v, nel punto P,
il flusso che attraversa una superficie chiusa e riferito allÆunitÓ di
volume; dove la superficie racchiude un volume sufficientemente piccolo (sempre
ai fini della possibilitÓ di poter utilizzare il calcolo differenziale) preso
nellÆintorno del punto dato:
(45)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() Ā ,
Ā ,
dove:
(46)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
essendo dS la superficie
chiusa che delimita il volume elementare dV,
il quale comprende il punto P = O + r, con O punto origine arbitrario e dA
una suŁperficie elementare aperta (notiamo che stiamo usando gli aggettivi
ōapertoö e ōchiusoö nel senso fisico e non nel senso in cui la distinzione
viene usata nella teoria degli insiemi).
Si dimostra:
(47)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
essendo V un volume
arbitrario, dove in ogni punto di esso Ķ definito lÆoperaŁtore č, e S Ķ la superficie chiusa che lo
contorna e in ogni punto della quale Ķ definito il vettore v.
Questa importante uguaglianza, che trasforma
un integrale di volume in un integrale di superficie, esteso a tutta la
superficie che circonda il dato volume, Ķ nota come la ōrelazione di Gaussö.
Ricordiamo che la divergenza, come il
gradiente, Ķ un ente assoluto, cioe indipendente dal sistema di coordinate
scelto e quindi invariante per arbitrarie trasformazioni di coordinate.
Consideriamo un esempio, estremamente
importante per le nostre sucŁcessive applicazioni fisiche.
Supponiamo di voler verificare la (47) in un
caso particolarmente sempliŁce, e calcoliamo prima la divergenza di un campo
vettoriale della forma
(i)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ E = k r n r
e proponiamoci, successivamente, di trovare
il valore di n per cui la divergenza risulti identicamente nulla.
Usando una nota identitÓ, avremo:
div (k r
n r) = k (r n div rĀ +Ā r ū grad
r n ) =
(ii)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀ = k (3r
n +n r n-1 r ū grad r) = k (3r n +n
r ū r r n-2) = k (3 + n) r
n
quindi, la divergenza Ķ sempre ben definita, con lÆesclusione (nel caso
che sia n < 0) del punto r = 0; escludendo
tale punto, la divergenza Ķ identicamente nulla per n = -3, cioĶ si ha:
(iii)ĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]()
Verifichiamo, ora, la relazione di Gauss per
una sfera di raggio r = R con
un campo della forma (i),
per n ╣ - 3.
Il primo membro della (47), con E al
posto di v, per il risultato (ii), vale:
(iv)ĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]()
(con il segno 0+ intendiamo escludere dallÆintegrazione il
punto r = 0).
Per n = -3, il primo membro della
(47), per il risultato (iii),
Ķ nullo.
Il secondo membro della (47), vale
(ricordando la definizione di angolo solido: ![]() ):
):
(v)ĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
la precedente relazione vale qualunque sia il valore di n.
Abbiamo verificato lÆuguaglianza dei due
membri della (47), con questa forma particolare di campo, per qualunque valore
di n diverso da -3; mentre lÆuguaglianza
sembra non valere per n = -3.
Ma ricordiamo che nellÆintegrazione di volume
avevamo escluso un inŁtorno dellÆorigine, ancorchķ arbitrariamente piccolo; punto
origine che non interviene, invece, nellÆintegrale di superficie.
Per n >
-3
il flusso, come
dato dalla (v), tende a zero
allÆorigine e quindi il punto origine non dÓ alcun contributo al flusso; per n < -3, allÆorigine si ha una
sorgente infinita, per cui il flusso calcolato includendo lÆorigine diverŁgerebbe
anchÆesso; per n = -3 il flusso, includendo
lÆorigine Ķ costantemente uguale a 4pk, il che significa che
lÆorigine Ķ lÆunica sorgente del campo, mentre negli altri casi dobbiamo
immaginare delle sorgenti continuamente distribuite nel campo.
Se ne deve concludere che:
ōla legge dellÆinverso del quadrato delle distanze Ķ la sola legge compatiŁbile con lÆidea di particellaö.
Quindi, il valore n = -3, che sopra abbiamo stabilito quale
condizione unica per avere una divergenza dappertutto nulla, Ķ
solo una condizione neŁcessaria ma non sufficiente. La condizione diventa anche
sufficiente quando, allÆinterno del volume considerato, non vi siano sorgenti
per il campo o le sorgenti siano tali che la somma algebrica delle loro
intensitÓ sia nulla.
Se, come si usa fare nelle applicazioni
fisiche, si definisce la divergenza con la (45), ne segue che bisogna andare
cauti nellÆidentificare la divergenza di un vettore con il prodotto scalare
dellÆoperatore nabla per il vettore di campo, in quanto i domini di
integrazione dei due integrali sono diversi.
Se in ogni punto del campo si ha div v = 0, allora si dice che il
campo Ķ ōsolenoidaleö, ovvero ōconservativo
per il flussoö.
Una formula analoga alla relazione di Gauss
si pu“ dimostrare per la circuitazione, se introduciamo il vettore:
(48)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ rot
v = č ┘ vĀĀ .
Considerando la circuitazione di v
lungo un circuito chiuso:
(49)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() ,
,
con un poÆ di algebra si pu“ scrivere:
(50)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ dC = rot v ū dS Ā,
a partire dalla quale si arriva ad unÆaltra importante uguaglianza,
valida per qualunque campo vettoriale, nota come ōrelazione di Stokesö:
(51)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ ![]() .
.
CioĶ il flusso del rotore di v
attraverso una superficie S Ķ uguale alla circuitazione di v
lungo la linea chiusa l,
che rappresenta il contorno della superficie S; in altre parole, il
flusso del rotore dipende solo dal contorno della superficie e non dipende,
invece, dalla forma o dallÆestensione della superficie stessa.
Con tale relazione un integrale di superficie
pu“ essere calcolato per mezzo di un integrale di linea e viceversa.
Anche qui bisogna considerare le possibili
eccezioni dovute alla diversa definizione dei domini di integrazione.
Se, in tutti i punti del campo, si ha rot v (r)
= 0, allora il campo si dice ōirrotazionaleö.
Nel caso che il campo vettoriale sia un campo
di forza la condizione di irrotazionalitÓ viene a significare che il lavoro
compiuto lungo una linea chiusa Ķ nullo e che quindi il campo Ķ conservativo
per il lavoro e ci“ implica lÆesistenza di una funzione potenziale.
Nel caso che il campo vettoriale rappresenti
il campo delle velocitÓ in un fluido, in condizioni stazionarie di moto, la
condizione di irrotazionalitÓ significherÓ lÆassenza di vortici.
Ma, in ogni caso, la condizione rot v (r)
= 0 implica lÆesistenza di un campo scalare, detto, appunto, ōpotenziale
scalareö j (r), tale che:
(52)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ grad j (r) = v (r)Ā .
Analogamente, la condizione div v (r)
= 0 implica lÆesistenza di un ōpoŁtenziale vettoreö,
definito a meno del gradiente di una funzione scalare; questo deriva dal
fatto che, necessariamente, per qualunque campo vettoŁriale v (r), si ha:
(53)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ div
rot v (r) = č ū č┘ v (r) = 0Ā ,
(purchķ gli operatori siano definiti nei punti considerati) e per
qualunque funzione scalare j :
(54)ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ rot grad jĀ = č ┘ č jĀ =
0.
Applicazioni alla meccanica razionale
Chiariamo che con il termine ōMeccanica Razionaleö intendiamo la mecŁcanica
di Newton nellÆinterpretazione di dÆAlembert (secondo noi la pi∙ adeŁrente allo
spirito e alla lettera dei ōPrincipiaödi
Newton), diametralmenŁte opposta a quella successivamente affermatasi sulle
orme di Eulero e di Lagrange.
La prima Ķ una scienza che non fonda i suoi
principi matematici sulle leggi empiriche ma che, al contrario, si propone di
spiegare le leggi empiriche a partire dagli ōelementiö
razionalmente definiti da opportune convenzioni linguistiche basate su
modelli semplici e verificabili.
Pensiamo che il calcolo geometrico di Peano
sia lo strumento pi∙ adatto per una tale concezione della meccanica.
Consideriamo un insieme di sistemi di forze
(cioĶ di formazioni di seconŁdo grado, nel seguito, lÆabbrevieremo con F2 e simili abbreviazioni useremo per le altre formazioni); indicando
con il segno = lÆequivalenza meccanica di due sistemi di forze, con il segno +
la sovrapposizione meccanica di due sistemi, con il segno 0 un sistema in
equilibrio meccanico, i sistemi di forze costituiranno un sistema lineare. Il
numero delle dimensioni di tale sistema (cioĶ il numero dei parametri necessari
e sufficienti per descriverlo completaŁmente) si dice ōnumero dei gradi di libertÓ del sistemaö; p. es., per un corpo
rigido esso vale 6.
Un sistema di punti materiali, ovviamente,
non Ķ un sistema lineare, dal momento che la sua derivata Ķ un vettore e non
pi∙ un punto materiale, anche se i vettori sono un sottosistema di un sistema
lineare costituito dalle F1.
Se ![]() ĀĶ un sistema di punti materiali, converrÓ
considerare la F2:
ĀĶ un sistema di punti materiali, converrÓ
considerare la F2:
![]() Ā,
Ā,
essendo O un punto
arbitrario.
La meccanica razionale non Ķ altro che la
teoria matematica che collega tra loro tali due sistemi di F2 (forze e bipunti). Come giÓ detto, il calcolo geometrico, come
sviluppato dal Peano, Ķ, a nostro avviso, la pi∙ semplice e, nello stesso
tempo, la pi∙ completa di tali teorie matematiche; per di pi∙, ha il vantaggio
di restare ancorato alle effettive operazioni fisiche che si possono compiere
sui sistemi fisici. Anzi, per le stabilite corrispondenze fra simboli ed enti
fisici, non ci sarebbe altro da aggiungere, se non quello di risolvere
determinati problemi concreti.
Dal punto di vista della matematica, nulla
vieta di considerare un sisteŁma di punti materiali come variabile (p. es., nel
tempo); ma, dal punto di vista della fisica, Ķ necessario che ci si possa
accorgere della loro variabilitÓ.
Per accorgersene bisognerÓ essere in grado di
misurare certi parametri numerici che rappresentino determinati rapporti tra
grandezze della stessa specie.
Un punto materiale, oltre alla massa che
supponiamo di sapere come misurare, non ha altri parametri numerici. Noi
possiamo misurare solo le distanze di esso da altri punti. Empiricamente ci
accorgiamo che, per individuarlo uniŁvocamente (in un determinato istante),
occorrono quattro parametri (massa compresa). Quindi dobbiamo scegliere quattro
formazioni geometriche arŁbitrarie per individuarlo. LÆalgebra che ne viene
fuori, qualunque sia il tipo di riferimento che vogliamo scegliere, non sarÓ
diversa. Ma, per certi probleŁmi particolari, alcune scelte possono risultare
pi∙ adeguate di altre.
Intenderemo, per riferimento, un ben
determinato sistema fisico. Se si immagina che tale sistema di riferimento sia
fissato una volta per tutte, non sarÓ necessario menzionarlo; ma questo non
significa che sia scomparso.
Ma, ripetiamolo, per tirare fuori conclusioni
di ordine generale, non saŁrÓ necessario usare le coordinate, tranne che per
qualche esempio concreto; infatti, tutto quello che si pu“ dire in generale
sugli enti fisici, lo si pu“ diŁre senza farne uso; le eventuali diversitÓ, che
si dovessero riscontrare nelle formule che descrivono la stessa fisica, possono
solo dipendere dalla loro parŁticolare rappresentazione in un dato sistema di
coordinate, e non possono essere diversitÓ degli enti fisici; in un linguaggio
assoluto tali diversitÓ devoŁno scomparire; per cui perdono di significato
termini quali: interpretazione attiva e passiva di una trasformazione, quantitÓ
covarianti e controvarianti, e ogni altro termine legato alla particolare
rappresentazione.
Le esposizioni della meccanica classica,
quasi sempre, cominciano col supporre che il sistema di riferimento debba essere
inerziale; ma poi si troŁvano in difficoltÓ nel cercare di stabilire che cosa
sia un sistema inerziale (naturalmente, questo vale anche per la teoria della
relativitÓ ristretta).
Qualcuno dice che Ķ inerziale un sistema di
riferimento in cui valgano le leggi di Newton, ma poi si aggiunge che tali
leggi valgono solo in un sistema inerziale e, cosņ, si chiude il circolo!, a
parte il fatto che, con la locuzione ōleggi
di Newtonö, si intendono cose assolutamente lontane
dalle idee di Newton. Infatti si intendono: la relazione F = ma , e il principio di azione e reazione
inteso nellÆaccezione ōforteö, cioĶ che le forze tra due punti materiali siano
vettori uguali ed opposti e, in pi∙, giacciano sulla stessa linea dÆazione
individuata dalla retta che congiunge i due punti materiali. Vedremo pi∙ avanti
che cosa implicano tali richieste.
Altri dicono che un sistema Ķ inerziale se si
muove di moto traslatorio uniforme rispetto al sistema delle stelle fisse; ma,
siccome tale sistema non e certamente inerziale, si aggiunge che lo Ķ solo
approssimativamente. Quanto buona sia tale approssimazione e per quali sistemi
di forze debba ritenersi valida, nessuno pu“ essere in grado di dirlo.
Per tale ragione, per fondare la meccanica di
Newton, proveremo a non nominare i sistemi inerziali; del resto Newton ha
fondato la sua teoria senza che mai gli balenasse lÆidea che tali inconoscibili
enti potessero servire a qualcosa, visto che mai li menziona! Noi,
nellÆincertezza, proveremo a vedere fino a che punto si pu“ andare avanti senza
nominarli.
Ricordiamo che Newton non parla mai di punti
materiali ma di corpi. Il punto materiale Ķ stato inventato solo molto tempo
dopo (qualcuno ne attribuisce lÆintroduzione a Eulero anche se lo stesso parla
ancora di corpi) come idealizzazione di un corpo, nel caso in cui i suoi gradi
di libertÓ interni non influiscano sul fenomeno in istudio. In tal caso si pu“
sostituire il corpo con il suo baricentro; anche se spesso non pu“ essere
esattamente determinato sperimentalmente.
Se lÆeffetto delle forze interne non puo
essere trascurato, si pu“ pensare di suddividere, idealmente, il corpo in parti
opportune, in modo tale che per ognuna di tali parti, in relazione al fenomeno
studiato, si possano trascurare i gradi di libertÓ interni. Per tali parti
useremo il nome di ōparticelleö.
Dal momento che le forze agiscono tra punti
(nel senso sopraspecificato), esse devono essere indicate da bipunti e non da
vettori.
UnÆultima avvertenza Ķ necessaria: la
variabilitÓ nel tempo deve intenŁdersi rispetto a un tempo omogeneo locale.
Quindi quella parte della fisica che pu“
essere descritta con dei numeri si riferisce sempre ad un dato sistema di
riferimento (fisicamente determinato) che sottintende anche il modo di misurare
il tempo, almeno localmente, oltre alle unitÓ di lunghezza di area e di volume.
Per collegare gli esperimenti eseguiti
allÆinterno di un dato riferimento con gli esperimenti di altri osservatori,
che procedono alle loro osservazioni relativamente ad altri riferimenti,
bisognerÓ fare altre ipotesi; da verificare, se possibile, sperimentalmente.
Ma, in ogni caso, la teoria che li collega non pu“ avere alcuna influenza sulla
fisica di un qualsiasi osservatore; al massiŁmo, costui potrebbe preferire una
matematica piuttosto che unÆaltra, quando risultassero rilevanti gli scambi di
esperienze tra tali ipotetici osservatori.
***
Sia ![]() , una F1 che
rappresenti un sistema di particelle che, per brevitÓ, chiameremo ōcorpoö; indicheremo con
, una F1 che
rappresenti un sistema di particelle che, per brevitÓ, chiameremo ōcorpoö; indicheremo con ![]() la sua massa, con
la sua massa, con ![]() il suo baricentro. Supporremo, per il momento, che le mi siano costanti nel tempo,
ma che le distanze relative tra le particelle del corpo siano variabili nel
tempo come localmente definito.
il suo baricentro. Supporremo, per il momento, che le mi siano costanti nel tempo,
ma che le distanze relative tra le particelle del corpo siano variabili nel
tempo come localmente definito.
Consideriamo il bipunto b
= OB, che
possiamo anche scrivere b
= O (B - O) = O r,
e che chiameremo: la ōlinea istantanea del baricentro, rispetto ad Oö; diremo
che r Ķ il vettore di tale linea o ōraggio
vettoreö.
Pi∙ in generale, diremo che bi
= OBi Ķ la linea di BiĀ rispetto ad O e che ri = Bi - O Ķ
il suo raggio vettore.
Chiameremo:
Bi (t)
Bi (t + Dt) la ōlinea dello spostamento di Bi (t) nel tempo Dtö; il suo vettore lo chiameremo
ōspostamentoö.
Per Dt sufficientemente piccolo si
ha:
![]() Ā;
Ā;
![]() Ķ la ōvelocitÓ della particella Biö.
Ķ la ōvelocitÓ della particella Biö.
La F2: ![]() Ārappresenta in modo
assoluto, cioĶ indipenŁdentemente dal riferimento, la somma delle quantitÓ di
moto delle singole particelle. Essa si pu“ scrivere, se O Ķ un punto arbitrario:
Ārappresenta in modo
assoluto, cioĶ indipenŁdentemente dal riferimento, la somma delle quantitÓ di
moto delle singole particelle. Essa si pu“ scrivere, se O Ķ un punto arbitrario:
![]() T
T![]() Op +Tc Ā.
Op +Tc Ā.
Chiameremo p la ōquantitÓ di moto totaleö del corpo (per definizione Ķun ente
assoluto, essa diventa una quantitÓ quando si assegnino le opportune unitÓ di
misura). E c Ķ il ōmomento
angolare totaleö del corpo relativamente al punto O.
Consideriamo la F2 (derivata della
precedente): ![]() Ā(ōsisteŁma delle forzeö che agiscono
sulle singole particelle del corpo), che possiamo anche scrivere:
Ā(ōsisteŁma delle forzeö che agiscono
sulle singole particelle del corpo), che possiamo anche scrivere:
![]() T
T![]() Of +T
Of +T![]() Ā,
Ā,
f Ķ la
ōrisultanteö delle forze relative che
agiscono sul corpo e ![]() Āil ōmomento delle forzeö relativo al punto O.
Āil ōmomento delle forzeö relativo al punto O.
Anche se f = 0, il corpo pu“ avere,
complessivamente, un moto acceleraŁto intorno al baricentro, oltre a un moto
traslatorio uniforme del baricentro, che si aggiunge (algebricamente) a tutte
le particelle (in questo caso ![]() ĀĀsarÓ un bivettore, cioe
una coppia). Ovviamente, un moto intorno al baricentro pu“ aversi anche quando f
= 0 e p = 0; nel caso particolare di un corpo rigido, si tratterebbe di
un moto rotatorio uniforme (spin).
ĀĀsarÓ un bivettore, cioe
una coppia). Ovviamente, un moto intorno al baricentro pu“ aversi anche quando f
= 0 e p = 0; nel caso particolare di un corpo rigido, si tratterebbe di
un moto rotatorio uniforme (spin).
Notiamo che la relazione che abbiamo scritto
sopra Ķ unÆidentitÓ alŁgebrica e vale qualunque sia il punto O; in particolare, vale se al posto di O mettiamo il baricentro del corpo B, quindi:
![]() T
T![]() Ā,
Ā,
essendo, ![]() , la derivata temporale dellÆeventuale ōmomento angolare intrinseŁcoö (brevemente:
ōspinö). Quindi:
, la derivata temporale dellÆeventuale ōmomento angolare intrinseŁcoö (brevemente:
ōspinö). Quindi:
Of +T![]() Ā= Bf + T
Ā= Bf + T![]() Ā.
Ā.
OĀ anche:
![]()
(ricordiamo che r Ķ
la coordinata del baricentro del corpo rispetto ad O).
Dalle precedenti definizioni si pu“
concludere:
ōPer qualunque
osservatore la forza f (in quanto ente assoluto) resterÓ la stessa anche se per i vari
osservatori potrÓ cambiare la loro classificazione tra ōforze effettiveö e
ōforze di inerziaö.
Ma questo non significa che non debbano
cambiare i parametri con i quali i vari osservatori individuano tale forza,
ognuno nel proprio riferimento.
Per quanto riguarda il momento delle forze,
lÆosservatore baricentrico pu“ dire che Ķ assoluto, in quanto dipende dalle
forze che si esercitano sulle particelle del corpo; particelle che gli appaiono
girargli attorno con diverse velocitÓ e accelerazioni, ed Ķ giusto uguale a ![]() ; e
potrÓ dire che gli altri osservatori
ne vedono uno diverso solo a causa della loro diversa posizione.
; e
potrÓ dire che gli altri osservatori
ne vedono uno diverso solo a causa della loro diversa posizione.
Se un qualunque osservatore si convince che
non ha alcun senso la ōquiete assolutaö, perchķ non verificabile
empiricamente, potrÓ sempre assumere, in ogni caso, come leggi universali del
moto, lÆespressione:
![]() Ā= Of +T
Ā= Of +T![]() Ā+ T r ┘ f ,
Ā+ T r ┘ f ,
e non si preoccuperÓ di sapere se la forza e la coppia che misura siano
effettive o apparenti (dÆinerzia).
La relazione che abbiamo scritto vale,
ovviamente, anche per una sola particella (un corpo piccolo!), qualunque sia
lÆosservatore O e qualunque sia il
suo riferimento, purchķ le forze siano quelle da lui misurate e non quelle da
lui ipotizzate, eventualmente potra aversi ![]() = 0, se la ōparticellaö
Ķ un corpo effettivamente ōpiccoloö in
base alle varie misure sperimentali, indipendentemente dalla sua estensione
geometrica.
= 0, se la ōparticellaö
Ķ un corpo effettivamente ōpiccoloö in
base alle varie misure sperimentali, indipendentemente dalla sua estensione
geometrica.
E dirÓ che:
ō![]() Ķ il sistema ōassolutoö
di forze che agisce sul corpo; f ne Ķ
la sua risultante; s Ķ lo spin del corpo, essendone
Ķ il sistema ōassolutoö
di forze che agisce sul corpo; f ne Ķ
la sua risultante; s Ķ lo spin del corpo, essendone ![]() Āla sua derivata
temporale (coppia di forze) che dipende dalla posizione relativa di tutte le
altre particelle del corpo; r ┘ p Ķ il momento
angolare del corpo relativo ad O; e la somma di questi ultimi due termini, c, Ķ il momento angolare totale del corpo rispetto ad Oö.
Āla sua derivata
temporale (coppia di forze) che dipende dalla posizione relativa di tutte le
altre particelle del corpo; r ┘ p Ķ il momento
angolare del corpo relativo ad O; e la somma di questi ultimi due termini, c, Ķ il momento angolare totale del corpo rispetto ad Oö.
Supponiamo che si abbia ![]() = 0; perchķ ci“ si verifichi Ķ necessario che siano
separatamente nulli il vettore f e il bivettore T
= 0; perchķ ci“ si verifichi Ķ necessario che siano
separatamente nulli il vettore f e il bivettore T![]() .
.
Esaminiamo il caso pi∙ semplice in cui
lÆuniverso sia costituito solo da due particelle mA, nB.
Si avra:
![]()
cioe:
ōle forze
reciproche sono uguali e contrarie ed agiscono nella retta diABö.
Anche nel caso di molte particelle vale la
conclusione che se ![]() = 0 deve valere il principio di azione e reazione
nellÆaccezione forte, per cui possiamo identificare
= 0 deve valere il principio di azione e reazione
nellÆaccezione forte, per cui possiamo identificare ![]() Ācon il sistema di
forze esterne al corpo; e se
Ācon il sistema di
forze esterne al corpo; e se ![]() = 0 diremo che il corpo Ķ isolato. Se ne deduce che:
= 0 diremo che il corpo Ķ isolato. Se ne deduce che:
ōsolo un
sistema di assi, fisso rispetto al baricentro di un sistema isolato, pu“ essere
inerzialeö
e quindi, rigorosamente, solo lo pu“ essere
un sistema di riferimento fisso rispetto al baricentro dellÆuniverso ammesso
che questo sia finito.
Formalmente:
ōIn un sistema
isolato le forze, di qualunque natura esse siano, agiscoŁno sempre lungo le
rette che congiungono le particelle, dipendono solo dalla distanza relativa tra
le due particelle e le reciproche forze sono sempre uguali e contrarieö.
Possiamo asserire qualcosa, senza ricorrere
ad alcuna legge empirica, come del resto abbiamo fatto finora, sulla forma
della dipendenza della forza dalla distanza relativa tra le particelle? Le
leggi empiriche, in ogni caso, ci potrebbero dare solo informazioni molto
approssimate.
Sappiamo giÓ la risposta se ricordiamo le
considerazioni che abbiamo fatto intorno alla relazione di Gauss:
ōla sola
possibilitÓ per la legge di forza tra particelle, nello schema deŁmocriteo di
atomi e vuoto, Ķ la legge
dellÆinverso del quadrato della distanzaö.
Notiamo che finora non abbiamo avuto bisogno
di alcuna legge empiricamente derivata; praticamente si sono date soltanto
delle definizioni; Newton, invece, assumeva come ipotesi che la legge dovesse
essere:
![]()
Anche se, come qualcuno sostiene, avendo egli
avuto modo di consultare gli inediti di Newton (vedi nota14), che lo
stesso Newton facesse risalire tale legge ai pitagorici (e secondo noi non Ķ
improbabile), tuttavia egli, nel rivolŁgersi ai suoi contemporanei, lÆassumeva
come ipotesi, giustificandola con il fatto che essa era in grado di spiegare i
moti planetari, le maree, e molti altri fenomeni naturali; tuttavia, non
giurava che essa potesse valere in generale e ipotizzava che, per le cariche
elettriche, le cui forze erano molto pi∙ intense, in futuro, si sarebbe potuto
osservare qualche deviazione; cosa che di fatto il futuro ha confermato. Non si
chiedeva la causa di tale legge, semplicemente perchķ, allo stato delle
conoscenze empiriche, non si potevano fare ipotesi (stante che lÆipotesi
cartesiana dei vortici era insostenibile, come meticoloŁsamente si era
impegnato a dimostrare). E, finchķ non si fossero osservati fenomeni rilevanti,
sarebbe stato assurdo fingere delle ipotesi non verificabili: lÆuna sarebbe
valsa lÆaltra, anche se matematicamente coerenti.
Ma vedremo, subito dopo, che, quando ci si
voglia riferire alle ōmisure sensibiliö,
lÆaffermazione di Newton non contrasta con il risultato teorico generale
che abbiamo sopra affermato, sullÆinevitabilitÓ della legge ![]() .
.
Molti interpretano la cautela, che qui
manifesta il grande scienziato, coŁme la propugnazione di un programma
deontologico, secondo il quale bisogna rifuggire dal cercare le cause e ci si
deve limitare alla semplice descrizione dei fenomeni; in altre parole, la
tassonomia dovrebbe sostituire la scienza, secondo il programma aristotelico.
***
Per quanto riguarda lo spin, se lÆosservatore
baricentrico lo vedrÓ variare nel tempo, dirÓ che le particelle del corpo sono
soggette a coppie esterne o, equivalentemente, che le forze che agiscono tra di
esse non agiscono lungo la retta congiungente le due particelle, e il principio
di azione e reazione, se dovesse valere, non lo potrebbe nellÆaccezione ōforteö.
Il problema del tempo locale non lo
disturberebbe, perchķ ci“ riguarda solo i numeri che dalle formule generali si
possono ricavare, quando si siano stabilite le opportune operazioni di misura e
le relative unitÓ di misura; mentre le relazioni, scritte sopra, sono in forma
assoluta.
Scriviamo le relazioni assolute rispetto a
due punti qualsiasi, O e OÆ, che possono, anche, rappresentare le
origini di due riferimenti in moto relativo qualsiasi. Per lÆidentitÓ algebrica
soprascritta si avrÓ:
![]() Ā.
Ā.
Se assumiamo che le fi
derivano solo dallÆinterazione tra tutte le particelŁle del corpo, secondo il
paradigma democriteo (tale ipotesi non Ķ verificabile empiricamente in tutta la
sua generalitÓ, ma solo entro i limiti consentiti dalle nostre operazioni di
misura), allora esse sono assolute, nel senso che non possono cambiare per
effetto del moto relativo dei due osservatori. Ma, naturalmente, varieranno nel
tempo, perchķ va cambiando la posizione relaŁtiva di tutte le particelle;
tuttavia la loro risultante e il momento totale delle forze, rispetto al
baricentro, rimangono invariati per tutti i possibili osserŁvatori; non cosņ
accade per le loro componenti (cioĶ le ōmisure
sensibiliö di Newton), le quali possono risultare diverse per i diversi
osservatori.
Spesso nei libri di meccanica si introducono
i concetti di ōforza assolutaö,
ōforza relativaö, ōforza di trascinamentoö,
ōforza complementareö.
Conviene esaminarne pi∙ da vicino il loro significato fisico, perchķ
queste forze apparenti possono modificare il risultato delle osservazioni
empiriche e ōapparentementeö violare
le conclusioni teoriche generali che abbiamo sopra asserito.
Supponiamo che due osservatori O e O′, i quali abbiano scelto terne ortogonali di riferimento diverse e in
moto relativo tra loro, considerino il moto di due punti arbitrari dello spazio
P e A; sia r = P - A il vettore relativo. Tale
vettore Ķ, in effetti, un ente assoluto in quanto indipendente da qualsiasi
osservatore. Tuttavia sono diversi i parametri con i quali i due osservatori
scompongono il vettore secondo le rispettive terne ortogonali scelte come
riferimento.
Esaminiamo prima il caso pi∙ semplice, in cui
i due osservatori usino unitÓ di misura simili (cioĶ compiano le stesse
operazioni di misura ognuno nel proprio riferimento; il confronto diretto tra
le unitÓ di misura dei due sistemi, in moto relativo, Ķ impossibile e quindi
non ha alcun significato fisico il chiedersi se le stesse operazioni fisiche
fatte nei due sistemi conducano a unitÓ di misura ōugualiö), per cui possono porre uguale ad 1 il
rapporto tra le lunghezze di uno stesso bipunto come misurate nei rispettivi
riferimenti.
In tali circostanze, i vettori unitari della
terna di un osservatore saranno legati a quelli dellÆaltro da unÆōisometriaö ŬĀĀ (Ŭ
Ŭ å
= ŬĀ å Ŭ = 1).
Quindi:
r = Ŭ Ŭ åĀ r.
Derivando rispetto al tempo si ha:
![]() Ā;
Ā;
per un teorema generale sulle isometrie,17 esiste un vettore w tale che ![]() Āqualunque sia il vettoreĀĀ r′ = Ŭ åĀ rĀĀĀ e, in particolare, il primo termine di
Āqualunque sia il vettoreĀĀ r′ = Ŭ åĀ rĀĀĀ e, in particolare, il primo termine di ![]() Ādiventa:
Ādiventa:
![]() Ā.
Ā.
DÆaltra parte, poichķ Ŭ Ķ operatore lineare sui vettori, si ha: se r = α i + β j + γ k
e r ′ = α i′ + β j′ + γ k′
(essendo i, j, k la terna ortogonale del riferimento di O e i′ , j′ ,
k′Ā quella di O ′ ),
![]() Ā.
Ā.
Nel riferimento di O ′,
per definizione, si ha: ![]() ; si trova che il termine
; si trova che il termine ![]() Ācoincide con la derivata di r
quando, a sua volta, O si volesse
considerare in quiete.
Ācoincide con la derivata di r
quando, a sua volta, O si volesse
considerare in quiete.
Per tale ragione, quando si consideri il caso
O = O ′ = A, si dice che ![]() Ārappresenta la ōvelocitÓ assolutaö di P, che
si divide in un primo termine w ┘ r
che si chiama ōvelocitÓ
di trascinamentoö e un secondo termine
Ārappresenta la ōvelocitÓ assolutaö di P, che
si divide in un primo termine w ┘ r
che si chiama ōvelocitÓ
di trascinamentoö e un secondo termine ![]() Āche si chiama ōvelocitÓ relativaö.
Āche si chiama ōvelocitÓ relativaö.
LÆoperatore ![]() Āviene spesso chiamato
la ōderivata rispetto agli assi mobiliö e si indica con
Āviene spesso chiamato
la ōderivata rispetto agli assi mobiliö e si indica con ![]() . Ma certamente per O
non Ķ assolutamente una deŁrivata (non lo Ķ neanche per O ′), lo sarebbe solo nel caso che O
si considerasse in quiete, rispetto ad un ipotetico sistema in quiete
assoluta; cosa, per“, che pu“ legittimamente pensare ognuno dei due
osservatori, attribuendo allÆaltro gli effetti inerziali.
. Ma certamente per O
non Ķ assolutamente una deŁrivata (non lo Ķ neanche per O ′), lo sarebbe solo nel caso che O
si considerasse in quiete, rispetto ad un ipotetico sistema in quiete
assoluta; cosa, per“, che pu“ legittimamente pensare ognuno dei due
osservatori, attribuendo allÆaltro gli effetti inerziali.
Per cui la
relazione di cui sopra, usualmente, si scrive
![]() Ā.
Ā.
Ci“ per dire semplicemente che ha quelle
componenti che avrebbe misurato O (assunto
come riferimento mobile relativamente a un ipotetico riŁferimento assoluto O ′) se, invece, si fosse considerato in quiete e alla quale si deve
aggiungere (se vuole ottenere il valore effettivamente misurato), per effetto
del moto relativo (che stranamente spesso si chiama moto assoluto) della sua terna, la velocitÓ che avrebbe
misurato O ′ se, a sua volta, il punto fosse stato
fermo rispetto al riferimento di O;
ma, naturalmente e allo stesso titolo, potremmo chiamare assoluta la
velocitÓ di P nel riferimento di O, per il semplice fatto che noi, come
ricordava Newton, possiamo solo osservare i moti relativi.
In effetti i due osservatori misurano la
stessa velocitÓ, varia solo la loŁro fittizia scomposizione in moto assoluto e
moto relativo, dal momento che nessuno dei due potrÓ mai sapere se Ķ fermo
rispetto allÆipotetica ōquiete asŁsolutaö
o meno; infatti, solo per un ben determinato fenomeno, del quale, per
ragioni puramente teoriche, si riesca a conoscere la legge del moto (cioĶ la reŁlazione
tra accelerazione misurata e forza ipotizzata), si pu“, entro gli errori di
misura, stabilire lÆapprossimata coincidenza con la, matematicamente deŁfinita,
ōquiete assolutaö,
che come abbiamo visto potrebbe solo significare il considerare fisso il baricentro
dellÆuniverso, ammesso che esista, ma tenendo presente che anche per tale
ipotetico riferimento, varrano le stesse consideŁrazioni che abbiamo fatto
prima, per il semplice fatto che il baricentro Ķ un punto e, invece, il sistema
di riferimento Ķ un quadripunto.
Forse la cosa migliore sarebbe quella di
abolire dal linguaggio della fisica termini quali ōassolutoö e ōrelativoö,
per il notevole deterioramento semanŁtico subito nel corso dei secoli,
quando appiccicati alla ōquieteö.
Derivando una seconda volta rispetto al tempo
si ottiene:
![]()
che con facili passaggi si pu“ riscrivere:
![]() Ā,
Ā,
questa viene usualmente scritta:
![]() Ā.
Ā.
Per le ragioni chiarite sopra, il termine a sinistra
del segno di identitÓ viene chiamato ōaccelerazione
assolutaö, la somma dei primi due termini a destra
ōaccelerazione di trascinamentoö,
il terzo termine a destra ōacceleraŁzione
complementareö e lÆultimo termine ōaccelerazione
relativaö.
Tutti questi termini vengono individuati nel
caso della terra: il primo, dei quattro termini a destra del segno =, si
fa corrispondere alle fluttuŁazioni che si osservano nella direzione che
individua lÆasse polare nel cielo delle stelle fisse, il secondo termine rappresenta
la forza centrifuga, il terzo termine Ķ lÆaccelerazione di Coriolis, lÆultimo
si ottiene per differenza, allo scopo di confrontarlo con il valore teorico,
dellÆaccelerazione di gravitÓ, quŁando ripulita dalle cosiddette forze ōapparentiö o ōdÆinerziaö, che tuttavia contribuiscono al valore
empiricamente misurato.
Ma Ķ importante notare che la cosiddetta
accelerazione ōassolutaö,
che poi, in effetti, Ķ lÆaccelerazione ōrelativaö
tra P ed O (od O ′, che Ķ lo stesso punto) Ķ veramente ōassolutaö, ma nel senso che tutti gli osservatori
ne misureranno sempre la stessa intensitÓ, indipendentemente dal loro moto che
pu“ solo alterare il valore (il solo direttamente misurabile) delle sue
componenti e la (apparente) classificazione tra forze effettive e forze di
inerzia.
In tal senso si pu“ accettare il (variamente
interpretato) principio di Mach dicendo, in accordo con gli antichi, che senza
materia non ci sono forze e senza forze non ci sono accelerazioni. Ma queste
sono proprio le ipotesi che stanno alla base della fisica di Newton: infatti
questÆultimo sostiene che la forza acceleratrice e la forza motrice sono nomi
diversi che diamo alla diversa apparenza sensibile di una sola e medesima cosa
che, ovviamente, deve restare invariata per effetto di una qualunque arbitraria
trasformazione.
DÆaltra parte, anche dal punto di vista della
matematica, risulta assoŁlutamente banale il fatto che non Ķ possibile
trasformare qualcosa se non si suppone che tale ōqualcosaö esista indipendentemente da ogni possibile trasformazione
che possiamo fare su di essa. P. es., la teoria della relativitÓ sostituisce,
nel ruolo di ōcosaö,
il quadrintervallo alla lunghezza; ma si trova in difficoltÓ
nellÆindividuare la ōcosaö da sostituire
alle forze che agiscono tra due corpi. Ne segue che Mach avrebbe dovuto
rivolgere la sua critica non alla fisica di Newton ma alla sua personale
interpretazione della stessa.
CollÆalgebra delle sostituzioni si possono
dedurre le relazioni pi∙ generali relative a due riferimenti che non siano
legati da unÆisometria. P. es., nel caso che uno dei due osservatori scegliesse
come unitÓ di lunghezza la distanza tra due punti, che per lÆaltro osservatore,
invece, apparissero in moto relativo arbitrario, si avrebbe una ōsimilitudineö,
variabile nel tempo; lo stesso avŁverrebbe nel caso che le operazioni di misura
del tempo fossero diverse per i due
osservatori e
si avesse un legame arbitrario t ′ = f(t).
Se, inoltre, uno dei due osservatori
assumesse definizioni operative di aree e di volumi diverse dalle usuali (cioĶ
diverse da S = l2 e
V = l3), si avrebbe una sostituzione pi∙
generale e, in tal caso, se uno dei due osservatori assumesse come valida la
geometria euclidea sarebbe costretto a concludere che quella dellÆaltro non lo
Ķ; e, naturalmente, viceversa.
Sulla identitÓ formale delle leggi della
meccanica e di quelle dellÆelettroŁmagnetismo, e sulla ingiustificata pretesa
che le leggi della meccanica debŁbano soddisfare le cosiddette trasformazioni
di Galileo rimandiamo ai nostri articoli, giÓ citati, nel numero di Aprile 1991
dei Quaderni di Mondotre. Per concludere:
Stimiamo che lÆaver trascurato il calcolo
geometrico del Peano nello stuŁdio della fisica sia stata un grandissima
perdita per lo sviluppo della scienza, speriamo, anche, che lÆopera di Peano
venga risuscitata, per cominciare, nella didattica, alla quale il Peano teneva
moltissimo.
NOTE
1
G. Peano Opere Scelte, a cura di U. Cassina,
Edizioni Cremonese, Roma, 1958.ĀĀ TORNA
2 G. Boscarino Peano e la filosofia, in Mondotre/Quaderni Ott. 1989. Siracusa.ĀĀ TORNA
3 A. Pagano. Su di unÆopera dimenticata di fisica di
Boggio e Burali ¢ Forti, in Mondotre/QuaderniĀ Ott. 1989. Siracusa; e dello stesso autore: Riflessioni sulla didottica della fisica, ibidem.
Apr. 1991.ĀĀ TORNA
4 S. Notarrigo, Il linguaggio scientifico dei presocrotici
analizzato con lÆideografia di Peano, in Mondotre/Quaderni, Ott. 1989, Siracusa.ĀĀ TORNA
5 S. Notarrigo, La scienza e la fede,
in Mondotre/Quaderni,
Apr. 1991. Siracusa.ĀĀ TORNA
6 G. Peano Opere Scelte, cit.
vol. III. pag. 142.ĀĀ TORNA
7 Ibidem, II, pag. 389.ĀĀ TORNA
8 A leggere i vari libri
sui fondamenti della matematica, circolanti in tutte le lingue,
sembra che tali assiomi siano i soli contributi di Peano che vengono
menzionati, anche se in modo concettualmente cosņ distorto che qualcuno,
addirittura, non riesce pi∙ a capire la differenza fondamentale che cÆĶ con gli
assiomi di Dedekind, per cui propone di assegnaŁre la primogenitura a
questÆultimo. Tale questione viene trattata da G. Boscarino. Le implicazioni filosofiche del concetto di
numero (Con un saqgio di Peano in Appendice), in Mondotre/Quaderni, Apr. 1991. Siracusa.ĀĀ TORNA
9 Vedi le citazioni pertinenti riportate
nellÆarticolo citato nella precedente nota.ĀĀ TORNA
10 Pensiamo che ogni
fisico, almeno in qualcuno dei momenti dedicati alla riflessione sulla sua
scienza, si sarÓ chiesto a cosa mai tali ineffabili enti possano servire. Una
usuale risposta Ķ che essi servirebbero a semplificare
la dimostrazione di importanti teoremi, o addirittura a dimostrarne altri non
ottenibili con altro mezzo. Ma tale risposta non sembra molto convincente,
visto che Peano riesce a fare tutto quello che serve senza usare tali
misteriosi enti: anzi, asserisce che ogni dimostrazione che usi lÆassioma di
Zermelo non Ķ affatto una dimostrazione ōsecondo
la comune accezione del vocaboloö.ĀĀ TORNA
11 Cfr. G. Peano. Calcolo Geometrico, Bocca Editori, Torino, 1888. In una successiva (pi∙
sintetica) esposizione del suo calcolo Peano scriveva:Ā ōEd invero questi vari metodi di calcolo
geometrico non si contraddicono fra loro. Essi sono le varie parti di una
stessa scienza, ovvero i vari modi sotto cui si presenta lo stess soggetto a
pi∙ autori, ciascuno dei quali lo
studia indipendentemente dagli altri.Ā
Poichķ il calcolo geometrico, come ogni altro metodo, non Ķ giÓ un sistema di convenzioni, ma un sistema di veritÓ.
Cosņ il metodo degli indivisibili (Cavalieri), degli infinitesimi (Leibniz),
delle flussioni (Newton) sono la stessa scienza, piu o meno perfetta, ed
esposta sotto forme diverseö . E pi∙ otre: ōģilĀĀĀĀĀĀĀĀĀĀĀ calcolo
geometrico ha tutte le proprietÓ del calcolo algebrico sui polinomi. ģ Questa
coincidenza dei due calcoli costituisce lÆimmenso vantaggio del metodo di
Grassmann. Esso permette di operare e ragionare conĀ un grande risparmio di sforzo e di memoria; poichie in questo
nuovo calcolo si opera come in una calcolo giÓ conosciuto. Questo metodo
risponde quindi al principio del minimo sforzo, il quale sussiste non solo in
meccanica, ma anche in didatticaö. Cfr. Peano, Opere Scelte, Vol. III. op.
cit., p. 168 e 172.ĀĀ TORNA
12 ╚ sorprendente la
disinvoltura con la quale un famoso fisico teorico pu“ scrivere le
parole di disperazione, qui appresso riportate, nella prefazione di un suo
libro, dove si illustrano i progressi che si sono compiuti, a partire dalla
teoria elettromagnetica di Maxwell: il quale ultimo, peraltro, aveva posto una
grandissima attenzione alle unita di misura, nel suo Trattato; ma, a distanza
di soli tre quarti di secolo da tale Trattato, il nostro moderno fisico
confessa candidamente: ōģpersonne nÆa pu me dire comment concilier
lÆadoption des unitķs ĀĀĀĀĀĀĀĀ ķlectromagnķtiques
rationelles avec la nķcessitķ pratique de se rķfķrer Ó des rķsultats
expķrimentaux exprimķs dans lÆancien systĶme dÆunitķs. En dķsespoir de cause, jÆy ai renoncķ.ö. Cfr. L. Rosenfeld, Theorie des electrons, Hermann, Paris, 1951. Notiamo che oggi non
si sente nemmeno il bisogno di
chiedere scusa per non sapere come collegare la teoria ai dati sperimentali!ĀĀ TORNA
13 Nella prefazione di uno
dei pochissimi libri di testo tradotti in italiano, dove si fa largo uso delle
forme esterne di Grassmann, si legge: ōIn
meccanica classica si utilizzano metodi e concetti matematici
molto diversi: equazioni differenziali e flussi di fase, applicazioni regolari e varietÓ, gruppi e algebre di Lie,
geometria simplettica e teoria ergodica. Molte delle moderne teorie matematiche
hanno avuto la loro origine in problemi di meccanica e in seguito hanno assunto quella forma astratta ed
assiomatica che ne rende cosņ difficile lo studioö. Vedi V. I. Arnold, Metodi matematici della meccanica classica, Editori
Riuniti, 1979: (per un testo didattico dove, invece, si usa lÆapproccio con i
quaternioni di Hamilton si veda: D. Hestenes, New Foundations for Classical Mechanics, Reidel, 1987). A nostro parere non Ķ lo studio che
viene reso difficile dallÆastrattezza, la quale se si volesse intendere come ōastrazioneö, invece, potrebbe semplificarlo, ma ne risulta difficile la
comprensione quando, dal mondo iperuraneo (sempre facile e bello per
definizione), si voglia scendere sulla terra per applicare il formalismo ai
concetti della fisica; che, se si devono conformare alla natura, potrebbero
risultare incompatibili con le elucubrazioni puramente astratte della nostra
mente, quando non sorrette dal riferimento alle operazioni fisiche, le quali,
spesso, vengono confuse con lÆōintuizioneö, che nessuno sa cosa mai
possa essere.ĀĀ TORNA
14 Cfr. Pierre Thuillier, Isaac
Newton, un alchimiste pas comme les autres,in La Recherche, n. 212,
Juillet ¢ Ao¹t, 1989.ĀĀ TORNA
15 Risulta a noi sorprendente
il fatto che quasi tutti attribuiscano a Newton tale strana idea dello spazio
assoluto in quiete assoluta, che ci sembra, piuttosto, debba attribuirsi
allÆassiomatizzazione di Eulero, comeĀ
mostreremo in altra pubblicazione.ĀĀ TORNA
16 Nella letteratura
moderna, per ragioni per noi incomprensibili, tale banale risultato, enunciato da Peano
nel suo ōCalcolo Geometricoö,
come una semplice applicazione, viene attribuito a Riesz.ĀĀ TORNA
17 C. Burali ¢ Forti, T.
Boggio, Meccanica Razionale, Lattes,
1921.ĀĀ TORNA