Entropia: tra caso e necessità
Salvatore
Notarrigo
Introduzione
Oggi viene generalmente riconosciuto che
l’impatto dello sviluppo economico sull’ambiente è uno tra i più grossi
problemi che l’umanità deve affrontare.
Tuttavia ancora manca un’analisi generale
sull’interazione tra econorma ed ambiente, anche perché ci si deve confrontare
con una situazione molto conflittuale in cui sono evidenti i due corni di un
dilemma: fermare lo sviluppo o aumentare l’inquinamento fino al crollo del
sistema, per non parlare degli interessi privati costituiti.
Alcuni ricercatori hanno contribuito a
sviluppare ingegnosi modelli basati principalmente sullo schema delle analisi
economiche di input‑output, la cui origine si può far risalire, indietro
nel tempo, al Tableau Économique di
Quesnay, che dopo Marx e Walras è stato brillantemente risuscitato, in tempi
più recenti, da Leontief.
Tuttavia, come anche viene riconosciuto dagli
stessi ricercatori che usano tale schema,1
esso soffre di alcune notevoli limitazioni e precisamente: lo schema è lineare
mentre il fenomeno da studiare è essenzialmente non lineare. In assenza di una
sottostante teoria generale, l’inclusione di effetti non lineari sembra del
tutto arbitraria e assomiglia ad un cieco processo di “data fitting” con molto
dubbie estrapolazioni.
Altri autori2 sostengono che il paradigma corrente delle scienze
economiche è incapace di affrontare gli aspetti irreversibili del processo
economico e sostengono che, in qualche modo, bisognerebbe includere nei modelli
economici la legge universale dell’“entropia” (Un’applicazione di tale
concetto al problema dell’interazione economia‑ambiente viene
considerata da Pagano in questo stesso numero di “Mondotre/Quaderni”).
Certamente ciò è necessario, tuttavia
pensiamo che senza una profonda rivoluzione nei correnti canoni epistemologici
non sia possibile una nuova scienza economica in grado di affrontare
coscientemente i problemi dell’oggi in vista di un nostro possibile futuro.
Non credo che il problema reale sia, come
alcuni sostengono, quello di abbandonare la visione meccanicistica, che si fa
risalire a Newton, come spesso erratamente si pretende, ma piuttosto, a mio
giudizio, si tratta di abbandonare il cieco empirismo oggi dominante in tutti
i settori della scienza moderna anche se spesso paludato con astratte e
complicate teorie matematiche.
Gli epistemologi contemporanei esprimono idee
molto confuse sull’argomento: c’è chi inneggia a Newton qualificandolo come
padre dell’empirismo e chi lo biasima come campione del meccanicismo!
La ragione di ciò sta, a mio giudizio,
nell’uso ambiguo e spesso senza significato con i quali si usano termini come
“caso”, “necessità”, “complessità”, ecc., come viene sottolineato
nell’articolo di Boscarino in questo stesso numero di “Mondotre/Quaderni”.
Il concetto essenziale per capire
quantitativamente la connessione tra questi termini è quello di “entropia”.
Ma quest’ultimo termine necessita anch’esso
di una precisa definizione, che ci permetta di capire i molti modi in cui il
suo concetto si manifesta.
Per arrivare a tale definizione bisogna
partire da Boltzmann, il quale già intravedendo il danno che l’empirismo
avrebbe provocato nella scienza ha condotto una strenua battaglia, purtroppo
perduta, nel corso della sua vita.3
Ai suoi tempi l’empirismo si andava
affermando anche nella fisica sotto il nome di “fenomenologia”, ma sentiamo
cosa Boltzmann dice in proposito:
“Si crede che
la fenomenologia possa rappresentare la natura senza in alcun modo andare oltre
l’esperienza, ma io credo che questa sia un’illusione. Nessuna equazione può
rappresentare un qualsiasi processo con assoluta accuratezza, ma sempre lo
idealizza, mettendo in evidenza alcuni tratti comuni e trascurando quei tratti
che sono diversi, andando così oltre l’esperienza. Che ciò sia necessario, se
noi vogliamo avere una qualche idea che ci permetta di predire qualcosa nel
futuro, segue dalla natura stessa del processo intellettivo, che appunto
consiste nell’aggiungere qualcosa all’esperienza così creando un’immagine
mentale che non è esperienza ma che perciò rappresenta molte esperienze.
Solo metà
della nostra esperienza è esperienza come dice Goethe. Più coraggiosamente si va oltre
l’esperienza, più generale sarà la comprensione che si otterrà della realtà,
più sorprendenti i fatti che si potranno scoprire, ma più facilmente si può
cadere in errore. Perciò la fenomelogia non dovrebbe vantarsi di non andare
oltre l’esperienza, ma dovrebbe semplicemente limitarsi ad avvertire di non
eccedere in tal senso.”4
E fu precisamente allo scopo di superare la
divaricazione tra modelli deterministici, come quelli della meccanica
newtoniana, e modelli indeterministici, come quelli della termodinamica dei
processi irreversibili, che Boltzmann inventò una nuova caratterizzazione del
concetto di “entropia”, già prima introdotto da Clausius per spiegare i
principi della termodinamica.
Nonostante che il concetto boltzmanniano di
entropia venga impiegato comunemente nella fisica e in molte altre scienze,
spesso sotto il nome di “informazione”, ancora si pensa che tale concetto sia
legato esclusivamente a certe operazioni con cilindri riempiti di gas perfetti
e relativi pistoni, come spesso si riscontra nei trattati elementari di
termodinamica, per cui molti sono convinti che tale concetto sia solo roba per
fisici e che non sia di alcuna rilevanza per affrontare i problemi
dell’economia e dell’inquinamento.
D’altra parte il termine, come tale, si
diffonde nella pubblicistica corrente e viene usato in modi assolutamente
lontani dal suo effettivo significato dando luogo a sorprendenti conclusioni!
Per cui ci è sembrato opportuno chiarirne il
significato per quel tanto che ci è possibile fare senza ricorrere troppo
pesantemente agli strumenti della matematica, che tuttavia sono necessari per
stabilire le relazioni quantitative tra le variabili in gioco.
Il caso e la necessità
Il concetto boltzmanniano di “entropia” è
strettamente legato ai concetti di “caso” e di “necessità”. Conviene prima
chiarire il significato di tali termini con degli esempi concreti.
La più elementare situazione in cui si usa il
termine “caso” e quella relativa al lancio di una moneta.
Noi non siamo in grado di predire con
certezza se il risultato del lancio sarà “testa” o “croce”.
Si potrebbe pensare che se noi fossimo in
grado di scrivere le equazioni del moto della moneta a partire dall’impulso
iniziale e dalle leggi della gravità e dalle leggi relative alla viscosità
dell’aria sarebbe possibile prevedere esattamente il risultato del lancio.
Ciò non si può certamente escludere! Ma
sarebbe un problema pressocchè insolubile. Ci conviene assumere semplicemente
che se lanciamo mille volte la moneta in circa metà dei casi si verificherà
“testa” e negli altri casi “croce”.
A partire da tale esperienza si potrebbe
concludere che quando diciamo “a caso” intendiamo confessare la nostra
ignoranza sulle cause che decidono il fenomeno. Quindi si può dare la seguente
definizione:
“Dire ‘a caso’ è lo stesso che dire ‘non
conosco tutte le cause che determinano il fenomeno’”.
Ma tale confessione di ignoranza non piace a
molti che perciò sono costretti a ipostatizzare il complesso delle cause ignote
con la parola “caso” che così diventa un nuovo ente metafisico oscuro e
onnipotente non molto dissimile dal “Fato” dei latini.
Tutte le altre situazioni che si riesce a
descrivere senza ricorrere all’intervento del caso si suole dire che avvengono
per “necessità”.
Con altre parole, tutto quello che è
possibile descrivere senza l’intervento del caso si chiama una situazione
“deterministica”, viceversa quello che necessita del caso si chiama una
situazione “indeterministica”.
Dopo di ciò molti continuano a spendere
inutili fiumi di inchiostro per stabilire se il mondo è assolutamente
deterministico, o assolutamente indeterministico o parzialmente deterministico
e parzialmente indeterministico.
Ora non c’è alcun dubbio sul fatto che nella
pratica della scienza ci sono situazioni che si descrivono con modelli teorici
assolutamente deterministici, altri con modelli assolutamente indeterministici
e altri ancora con modelli in parte deterministici e in parte indeterministici.
Per mostrare il labile limite che esiste tra
“caso” e “necessità” farò due significativi esempi.
Nelle applicazioni pratiche delle scienze
statistiche occorre riprodurre delle sequenze di numeri random (cioè sequenze
casuali, dette anche aleatorie). Tali sequenze di numeri vengono raccolte in
appositi manuali in modo che ognuno che ne abbia bisogno li possa facilmente
usare.
Vediamo, in teoria, come tali sequenze
possano essere generate mediante una serie ripetuta di lanci di una moneta o
equivalentemente di lanci di più monete, se si fa l’ipotesi che il risultato di
un lancio contemporeneo di n monete
equivalga a n lanci ripetuti di una
stessa moneta.
È noto che un qualsiasi numero
può essere scritto in forma binaria, assumendo un opportuno codice.
P. es., {000} = 0, {001} = 1, {010} = 2,
{011} = 3, {100} = 4, {101} = 5, {110} = 6, {111} = 7.
Nell’esempio precedente con sole due “cifre
binarie” (comunemente chiamate “bit”) {1 e 0} abbiamo potuto individuare otto
numeri che in base decimale vanno da 0 a 7, perché abbiamo scelto di formare
“parole” di solo tre bit, la ragione sta nel fatto che il numero dei modi in
cui si possono diversamente disporre le due cifre nelle tre caselle ordinate è n =
23 = 8. Se scegliamo di formare parole, p. es., con 40 bit
possiamo rappresentare 240 (cioè circa dieci milioni) numeri
diversi.
Allora lanciando 40 monete poste ordinatamente in riga, assegnando la cifra 1 all’evento “testa” e la cifra 0 all’evento “croce” e ripetendo ogni volta lo stesso procedimento, possiamo generare tutte le sequenze di numeri random che ci piace, compresi tra zero e dieci milioni, e il fatto che abbiamo usato il lancio delle monete ci assicura che le sequenze sono veramente “casuali”, cioè prodotte dal “caso”.
Con l’uso sempre più frequente dell’elaboratore
elettronico in ogni campo della scienza sorse la necessità di far produrre
all’elaboratore stesso le sequenze di numeri random.
Ora questo sembrava un grosso problema. Come
potrà mai una macchina assolutamente deterministica, tale per costruzione, generarare
sequenze di numeri random, che sono il paradigma dell’indeterminismo?
Perciò si tentò di utilizzare allo scopo il
“rumore di fondo” prodotto dai circuiti elettronici dell’elaboratore,
ritenendolo casuale. Ma quando le sequenze così generate venivano sottoposte
agli usuali test statistici si scopriva che le sequenze non erano perfettamente
casuali e perciò l’uso di tali sequenze comportava degli errori di valutazione
spesso intollerabili.
Altri metodi venivano studiati sempre con
scarso successo. Finché qualcuno, superando il paradigma che vuole caso e
necessità, determinismo e indeterminismo, come aspetti separati ed
inconciliabili della realtà, non propose un metodo assolutamente
deterministico per generare i numeri random che sono il paradigma
dell’indeterminismo e del caso!
Vediamo come si procede.
Supponiamo di avere un elaboratore
elettronico organizzato a “parole” di 40 bit (con semplici artifici di calcolo
si può usare allo scopo un personal computer che usualmente è organizzato con
“parole” di solo otto bit o in “byte” come più spesso si dice). Per poter
moltiplicare due numeri e mantenere la precisione associata alla parola di 40
bit il processore del calcolatore deve avere una parola di 80 bit, il risultato
della moltiplicazione verrà memorizzato scartando, dopo avere eseguito la
moltiplicazione, i 40 bit meno significativi e tenendosi invece i 40 bit più
significativi.
Supponiamo, invece, di tenerci come risultato
da memorizzare i 40 bit meno significativi e di scartare quindi i 40 bit più
significativi.
Partendo da un numero dispari iniziale di 40
bit, abbastanza grande, moltiplichiamolo per se stesso, usando tale inusuale
metodo di memorizzazione, e continuiamo a moltiplicare il risultato con il
risultato volta a volta precedente. Si otterrà una sequenza di numeri che ad
ogni test statistico risulterà assolutamente casuale.
Conclusione: da un procedimento assolutamente
deterministico abbiamo ottenuto una sequenza di numeri che si pensava si
potesse solo ottenere mediante processi assolutamente indeterministici come
quelli legati al lancio delle monete!
Vediamo ora l’esempio complementare dove a
partire da un processo assolutamente indeterministico (almeno teorizzato come
tale all’interno del paradigma quantistico) si può costruire una macchina
assolutamente deterministica, come un orologio, che è il paradigma di un
sistema deterministico.
Si abbia una sostanza radioattiva a
lunghissima vita media, in modo che l’attività media (cioè il numero di
decadimenti all’unità di tempo) sia con buona approssimazione costante nel
tempo per tutta la durata dell’esperimento. Supponiamo di avere a disposizione
una scala di conteggio che conta e visualizza il numero dei singoli decadimenti
della sostanza radioattiva (l’esperimento che stiamo descrivendo si può
attuare facilmente in un laboratorio didattico a disposizione degli studenti di
fisica). La teoria, corroborata dalla pratica, ci dice che il numero di
decadimenti registrati, p. es., in un secondo, chiamiamo n tale numero,
è proporzionale alla quantità della sostanza radioattiva ma, tuttavia, essendo
che il meccanismo di decadimento è assolutamente aleatorio, non sarà registrato
sempre lo stesso numero, se non casualmente, e si avranno sempre delle
fluttuazioni all’intorno del valor medio che sono circa uguali, come predice la
teoria e come si conferma sperimentalmente, alla radice quadrata del numero di
decadimenti registrati in un dato intervallo di tempo.
Cioè, se nell’intervallo di tempo
Δ t registriamo N eventi il valor medio del numero dei
conteggi nell’unità di tempo sarà ![]() .
.
Ora supponiamo di prendere una determinata
quantità di tale sostanza radioattiva in modo da poter registrare in media un milione
di decadimenti al secondo, e di prendere una scala di conteggio con un display
costituito da sette elementi decimali in serie, cioè il primo elemento decimale
fa scattare il secondo elemento di una unità ogni qualvolta abbia registrato
dieci decadimenti e quindi si riazzera automaticamente, il secondo elemento fa
scattare di una unità il terzo elemento ogni qual volta abbia contato dieci
unità, quindi ogni cento decadimenti, e così via fino al settimo elemento che
scatterà di una unità dopo ogni milione di decadimenti.
L’errore percentuale su un milione è, secondo
quanto detto sopra, circa ![]() cioè circa l’uno per
mille, conseguentemente l’errore nell’intervallo di tempo tra due scatti
successivi del settimo elemento decimale sarà di circa un millesimo di secondo,
per cui il settimo elemento della scala può servire da contasecondi con la
precisione di un millisecondo.
cioè circa l’uno per
mille, conseguentemente l’errore nell’intervallo di tempo tra due scatti
successivi del settimo elemento decimale sarà di circa un millesimo di secondo,
per cui il settimo elemento della scala può servire da contasecondi con la
precisione di un millisecondo.
Si può aumentare la precisione di tale
orologio costruito a partire da eventi elementari assolutamente casuali e quindi
indeterrninistici semplicemente aumentando la quantità di sostanza radioattiva
da porre sotto il contatore.5
Dai due esempi che sopra abbiamo esposto si
vede che il confine tra caso e necessità non sta nella natura delle cose ma
solo nel modo in cui guardiamo alle cose. In altre parole “caso” e “necessità”
non sono parole che possiamo usare in riferimento alla realtà ma solo al modo
in cui ce la rappresentiamo e tanto meno siamo autorizzati a studiarne
l’ontologia, avendo creato dei demoni che rispondono al loro nome.
Nella scienza teorica, in tutte le sue
branche, dalla fisica, alla biologia, alla sociologia, ecc., il paradigma di
una situazione assolutamente deterministica è quella che si può descrivere
matematicamente con una equazione differenziale, usualmente del secondo ordine.
Quando si riesce a scrivere un’equazione
differenziale per descrivere l’evoluzione di un dato fenomeno, si sa, perché
la matematica lo dimostra, che assegnate le “condizioni iniziali” l’andamendo
del fenomeno resta completamente determinato da qui all’eternità.
Per fare qualche esempio, prendiamone uno che
può capitare in un modello ecologico.
Consideriamo astrattamente un particolare
ambiente in cui vivono delle api. Facciamo l’ipotesi che la quantità di miele
prodotta in un assegnato intervallo di tempo, Δ t, da tutte le api sia costante nel tempo, e indichiamola con il
simbolo v, vogliamo calcolare la quantità di miele prodotta dopo un
certo tempo t a partire da una certa
data che assumiamo come origine dei tempi.
Sia Δ q la quantità prodotta
nell’intervallo di tempo Δ t,
sarà, per le ipotesi fatte:
(1) ![]() costante .
costante .
Poiché abbiamo supposto che v non varia nel tempo, è ovvio che possiamo
scegliere di prendere un intervallo di tempo piccolo a piacere e la equazione
(1) resterà sempre valida pur di scegliere Δ q
proporzionatamente piccolo per soddisfare l’equazione.
Quando Δ t e Δ q sono sufficientemente piccoli, tali
variazioni si confondono con quegli oggetti che i matematici chiamano
differenziali e che sono soliti indicare con il simbolo d al posto del simbolo Δ (in questo caso, essendo v costante, le variazioni coincidono sempre con i differenziali) per
cui la (1) si può riscrivere come:
(2) ![]() .
.
Il rapporto tra i due differenziali si chiama
la ‘derivata di q rispetto a t ’
e la (2) si dice un’equazione differenziale.
I matematici forniscono regole generali per
trovare la soluzione delle equazioni differenziali. Nel nostro caso la soluzione
generale è:
(3) q(t) = vt + q0
,
che ci dà la quantità di miele prodotta complessivamente al tempo t pur di conoscere la quantità iniziale q0 al tempo
iniziale che abbiamo assunto come origine dei tempi, t = 0.
In questo semplice caso tutti avrebbero
potuto dare la risposta giusta senza ricorrere a questi procedimenti
matematici. Ma ci sono casi più complicati in cui la risposta giusta si
ottiene solo usando tali procedimenti, che essendo del tutto generali valgono
anche per i casi semplici.
Infatti, complichiamo un poco il modello
precedente.
Supponiamo che v non sia costante
nel tempo ma che vari nel tempo con una legge del tipo (perché, p. es., la
quantità di fiori dell’ambiente dimuisce col tempo):
(4) v = v0 - g t ,
con g e v0 costanti nel tempo.
L’equazione differenziale ora diventa:
(5) ![]() .
.
La soluzione generale è:
(6) ![]() .
.
La curva che rappresenta la soluzione è una
parabola, la quantità di miele prodotta complessivamente raggiunge il suo
valore massimo al tempo ![]() e là si ferma perché a
partire da quell’istante la quantità prodotta nell’unità di tempo verrebbe a
essere negativa, ma ciò è impossibile, dato il significato reale del simbolo v.
e là si ferma perché a
partire da quell’istante la quantità prodotta nell’unità di tempo verrebbe a
essere negativa, ma ciò è impossibile, dato il significato reale del simbolo v.
Matematicamente ci sono soluzioni anche per
valori negativi di v e in altri
contesti possono avere significato, come per esempio nel caso della caduta di
un grave sotto l’azione della gravità che conduce alla stessa equazione differenziale,
in tal caso la costante g rappresenta l’accelerazione di gravità, la
variabile q, la distanza percorsa e la variabile v, rappresenta la velocità del grave che
può cambiare di segno a seconda che il grave va verso l’alto, per un impulso
iniziale, o verso il basso. Il vantaggio della matematica è proprio quello di
astrarre dalle particolari situazioni concrete e fornire formule generali che
si possono applicare in ogni circostanza indipendentemente dal significato dei
simboli.
Continuiamo a considerare astrattamente
l’equazione (5).
E prendiamo la variazione dei due membri
dell’equazione:
(7) ![]() .
.
Tenuto conto che la variazione di una
costante come, nel nostro caso, v0 e sempre nulla, prendendo la variazione sufficientemente piccola
con lo stesso argomento di prima arriviamo alla conclusione che, in questo
caso, la derivata della derivata (che si chiama la derivata seconda) della q(t)
è una costante e usando gli usuali simboli dei matematici l’equazione si può
scrivere:
(8) ![]() .
.
Questo è un esempio di equazione
differenziale del secondo ordine.
I matematici danno metodi generali per
risolverla, nel nostro caso, ovviamente la soluzione è data dalla (6) e sarà
perfettamente determinata a partire dalle condizioni iniziali, che si devono
supporre note, v0
e q0.
Questo significa che se conosciamo la
derivata seconda di q(t) rispetto al
tempo e le condizioni iniziali v0
e q0 possiamo conoscere il valore di q(t) ad ogni istante di
tempo.
Ecco un caso di determinismo assoluto.
Le cose dette precedentemente si
generalizzano a situazioni in cui g non è costante ma dipende a sua
volta da t, da q e da ![]() e anche al caso che
oltre a q intervengano altre variabili legate fra loro da una qualche
legge che lega le derivate seconde di ognuna delle variabili alle altre
variabili del sistema, in tale ultimo caso avremo un “sistema di equazioni
differenziali” una per ogni variabile.
e anche al caso che
oltre a q intervengano altre variabili legate fra loro da una qualche
legge che lega le derivate seconde di ognuna delle variabili alle altre
variabili del sistema, in tale ultimo caso avremo un “sistema di equazioni
differenziali” una per ogni variabile.
In ogni caso la matematica ci dice che, sotto
condizioni poco restrittive, si può trovare la soluzione generale del sistema
di equazioni differenziali che modellizza la situazione concreta e date le
condizioni iniziali è possibile, in modo assolutamente deterministico, predire
il valore di ognuna delle variabili a qualunque tempo passato o futuro.
Dopo avere dato un esempio di come si procede
nelle scienze teoriche mostriamo una situazione molto interessante dal punto di
vista teorico in cui un sistema assolutamente deterministico appare indeterministico
a seconda di come lo si guarda e di quando lo si guarda.
L’esempio riguarda un sistema di oscillatori,
ma potrebbe riguardare un qualsiasi altro fenomeno per cui si possa costruire
un modello che porta allo stesso sistema di equazioni differenziali; ci sono
molti casi in chimica, in biologia, in economia e persino in sociologia che
sono modellizzabili con lo stesso sistema di equazioni differenziali.
Il sistema di oscillatori è mostrato in Fig.
1.
Si hanno un certo numero n di masse, tutte uguali tra loro, legate l’una con l’altra con
delle molle, tutte uguali tra loro, le due masse poste alle estremità della
catena di oscillatori siano vincolate a stare sempre ferme.
Le leggi di Newton, assieme alle leggi
dell’elasticità, permettono di scrivere il relativo sistema di equazioni
differenziali, che qui non scriveremo.
I teoremi generali della matematica ci dicono
che assegnate le condizioni iniziali (in questo caso le posizioni e le velocità
di tutte le masse all’istante t = 0)
si può predire la posizione e la velocità di ogni singola massa ad ogni istante
futuro del tempo.
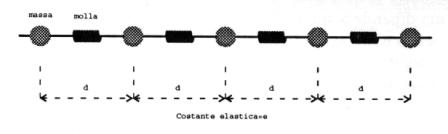
Fig. 1
Ci sono particolari condizioni iniziali per
cui le varie masse compiranno oscillazioni sinusoidali intorno alle loro
posizioni di equilibrio tutte con la stessa frequenza. Questi particolari modi
di oscillazione sono detti “modi normali” e la matematica ci dice che se gli
oscillatori vibranti sono in numero di n,
si avranno esattamente n modi normali.
Per qualunque altra combinazione di condizioni iniziali si avranno determinate
sovrapposizioni con diversi pesi degli n modi
normali.
Supponiamo di dare le seguenti condizioni
iniziali: all’istante t = 0 tutti gli
n oscillatori vibranti (cioè esclusi
i due alle estremità che per ipotesi sono vincolati a stare permanentemente
fermi) si trovino nelle loro posizioni di equilibrio, la velocità iniziale di
tutti gli oscillatori vibranti, tranne il primo della catena, è nulla. Il primo
oscillatore ha una velocità data, v0, che gli viene
comunicata all’istante t = 0 da un
impulso esterno.
Il sistema di equazioni differenziali è
facilmente risolvibile e possiamo calcolare tutto a qualsiasi istante di tempo.
Nella Fig.2 è graficata l’evoluzione
temporale della velocità del primo oscillatore, per un sistema di 100
oscillatori vibranti. I numeri riportati nella scala dei tempi sono relativi ad
unità scelte in modo da rendere il grafico indipendente dalle particolarità
meccaniche del sistema, precisamente una unità di tempo è stata posta uguale
a ![]() , essendo m la
massa del singolo oscillatore e k la
costante elastica delle molle e che chiameremo unt = unità naturale di tempo.
, essendo m la
massa del singolo oscillatore e k la
costante elastica delle molle e che chiameremo unt = unità naturale di tempo.
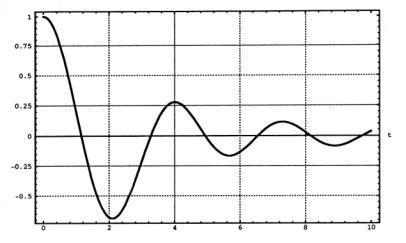
Fig. 2
Ora supponiamo di chiedere a un fisico di
proporre un modello matematico per spiegare questa figura senza dirgli come
essa è stata generata.
Egli subito penserebbe a un solo oscillatore
smorzato da forze di viscosità dipendenti dalla velocità e proporrebbe un
modello matematico per spiegare l’andamento della curva come il seguente:
(9) ![]() ,
,
dove a e b sono due
costanti da determinare “fittando” la curva, cioè trovando i migliori valori di
a e b che meglio adattino la
soluzione della (9) alla curva data.
Notiamo che nell’equazione del moto (9)
compare la derivata prima rispetto al tempo, che rende conto delle forze
dissipative di attrito.
E non potrebbe fare diversamente, perchè tale
modello è il più semplice che si possa immaginare! In base a tale modello
penserebbe, che essendovi delle forze di attrito, il sistema è irreversibile e
perciò parte della sua energia iniziale si va trasformando in calore facendo
aumentare l’entropia dell’universo in base ai principi della termodinamica.
Ma noi sappiamo che nel nostro sistema di 100
oscillatori accoppiati da molle non ci sono attriti, semplicemente perché non
li abbiamo inclusi nel nostro modello matematico e quindi non potremmo
accettare nemmeno le speculazioni metafisiche di Prigogine,6 il quale lega l’irreversibilità al fatto che
nell’equazione del moto compaiano termini con le derivate prime rispetto al
tempo (che rendono asimmetriche le leggi del moto rispetto all’inversione del
tempo), per la semplice ragione che nel nostro modello matematico queste non
ci stanno, per cui il sistema è assolutamente reversibile secondo la
definizione di Loschmidt.
Tuttavia il nostro modello è effettivamente
“irreversibile” ma in un altro senso che è più simile all’irreversibilità della
termodinamica.
Infatti guardiamo a come appare la curva
quando la osserviamo per tempi sufficientemente lunghi.
Nella Fig. 3 si vede la stessa variabile
della Fig. 2, ma dove con un opportuno cambio di scala possiamo osservare fino
a 1000 unt.
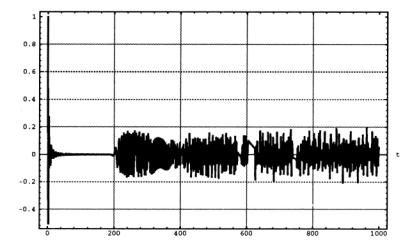
Fig. 3
Quello che prima vedevamo nella Fig. 2 ora,
nella Fig. 3, appare concentrato all’inizio del grafico, poi, nel periodo che
va circa da 50 unt a circa 200 unt, l’oscillatore appare
completamente fermo per poi risvegliarsi di nuovo con un andamento che a partire
dal tempo segnato da 400 unt rimarrà
mediamente sempre lo stesso fino all’eternità come si può dimostrare (qui non
lo dimostriamo perché la dimostrazione coinvolge una matematica piuttosto
complessa).
Quindi nonostante nel sistema di equazioni
differenziali che definiscono il nostro modello non compaiono le derivate prime
il sistema si comporta come un sistema termodinamico che procede
irreversibilmente verso una situazione di equilibrio apparentemente caotico.
L’errore di Prigogine sta nel confondere
l’irreversibilità come definita in meccanica con l’irreversibilità che si
definisce in termodinamica. Infatti il nostro sistema è meccanicamente
“reversibile” in quanto invertendo la “freccia del tempo”, come si usa dire,
le equazioni del moto restano le stesse, ma lo stesso sistema è
termodinamicamente “irreversibile” in quanto partendo da una determinata
condizione iniziale il sistema non tornerà più ad essa ma raggiungerà una
situazione apparentemente caotica con rapide fluttuazioni attorno a un valore
medio che è esattamente zero, se si guarda all’ampiezza delle oscillazioni o
alla velocità istantanea dell’oscillatore, naturalmente il valor medio
dell’energia sarà un valore costante, pari a un centesimo dell’energia totale,
valore che in meccanica statistica viene legato alla temperatura del sistema.
Il legame tra questo comportamento e
l’entropia di Boltzmann sarà considerato appresso, per il momento osserviamo
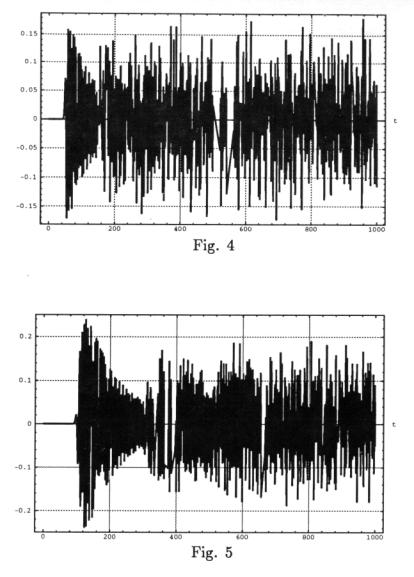
che il comportamento del primo oscillatore è praticamente identico, a quello
di tutti gli altri oscillatori della catena, come si vede dalle Figg. 4 e 5 che
mostrano, rispettivamente, l’andamento del cinquantesimo oscillatore e del
centesimo, cioè l’ultimo della catena.
Nella Fig. 4 vediamo che l’oscillatore posto
a metà della catena resta fermo fino a un tempo pari a circa 50 unt per poi cominciare a muoversi in
modo apparentemente erratico per tutti i tempi successivi. L’impulso iniziale
dato al primo oscillatore al tempo t = 0
non è ancora arrivato fino al tempo t » 50
unt.
Similmente nella Fig. 5 osserviamo che
l’ultimo oscillatore si mette in moto solo dopo circa 100 unt.
Questo comportamento sfata l’altro
pregiudizio, spesso difeso anche da illustri fisici,7 che in un sistema con forze di tipo newtoniano il
segnale, che stranamente viene confuso con l’interazione, si propaghi con
velocità infinita. A questo proposito è interessante vedere come si propaga
l’energia media nel nostro sistema come mostrato nella Fig. 6.
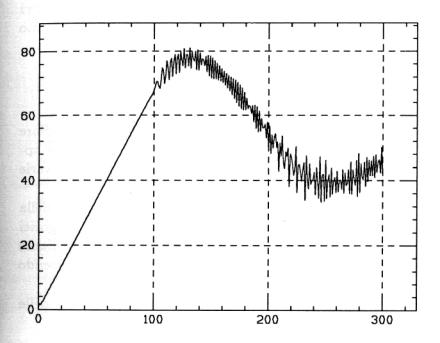
Fig. 6
Nella figura è graficato istante per istante,
in funzione del tempo, il punto dove si concentra l’energia cinetica media.
Si vede che fino all’istante t = 100
unt tale punto si propaga come una
particella con velocità costante, dopo di che comincia a oscillare fino a portarsi,
per tempi maggiori di quelli mostrati nel grafico, a un valore costante come se
tale particella fittizia si fosse fermata al centro della catena, cioè presso
il cinquantesimo oscillatore, a meno di piccole fiuttuazioni.
Naturalmente l’estensione del pacchetto
d’onda che si propaga come una particella si va continuamente allargando nel
tempo, fino a raggiungere il suo valore massimo vicino al settantesimo
oscillatore dove, come si vede dalla figura, la direzione del moto della
particella fittizia si inverte.
Per non riempire il testo con troppe figure
non mostriamo quest’ultimo comportamento che abbiamo descritto.
Anche perché le figure fin qui mostrate sono
sufficienti come oggettivi riferimenti per le cose che diremo sul concetto di
entropia che è l’argomento principale di questa nota.
Informazione ed entropia
Già fin dal tempo della civiltà sumerica si è
capito che una migliore conoscenza delle cose del mondo si poteva ottenere solo
quantificando opportune variabili e cercando le correlazioni numeriche
esistenti tra le varie grandezze.
La scuola pitagorica ci ha tramandato
notevoli conoscenze nell’uso della matematica per la comprensione del mondo che
ci circonda, anzi, i pitagorici sostenevano che il mondo reale è solo quello
che viene inquadrato mediante le correlazioni tra i rapporti numerici tra le
varie grandezze, il resto essendo soltanto caos sensoriale.
Il concetto elementare per ordinare
quantitativamente il mondo delle nostre esperienze è quello di “grandezza”.
Il paradigma di una “grandezza” è quello di
“lunghezza”.
Per poter definire una determinata grandezza
bisogna innanzitutto istituire un metodo per “confrontare” due grandezze della
stessa specie in modo da poter stabilire se le due grandezze sono eguali o
l’una è maggiore o minore dell’altra.
Quando si è istituito tale metodo di
confronto è possibile prendere un campione della grandezza data come unità di
misura, p. es., per le lunghezze, il “metro”, e definirne i “multipli” e i
“sottomultipli” mediante l’introduzione dei “numeri”. La possibilità di
stabilire multipli e sottomultipli è legata alla proprietà di “additività”
delle grandezze. In altre parole deve essere possibile “sommare” due grandezze
della stessa specie.
È possibile quantificare il “caso”?
Nel diciassettesimo secolo il gioco d’azzardo
era molto popolare in molti circoli alla moda della società francese. Si
giocava con i dadi, con le carte, con il lancio di monete, con la roulette,
ecc. e molti illustri matematici, come Pascal, Fermat, d’Alembert, de Moivre e
molti altri, si cominciavano ad interessare, dietro richiesta di alcuni
influenti giocatori, di inventare delle formule matematiche con le quali si
potessero calcolare le speranze di vincita in determinati giochi.
Tali matematici gettavano le basi di quel
ramo delle matematiche che oggi si chiama “teoria della probabilità”.
Chi per primo vide le profonde implicazioni
della definizione quantitativa di probabilità in ogni ramo della scienza fu
Laplace.
Nell’introduzione al “Saggio filosofico sulle probabilità” Laplace scrive:8
“...parlando
rigorosamente, quasi tutte le nostre conoscenze non sono che probabili; e anche
quelle pochissime che stimiamo certe, persino nelle scienze matematiche, ci
sono date dall’intuizione e dall’analogia, che, strumenti principali per
giungere alla verità, si fondano sulle probabilità. Perciò
il sistema intero delle conoscenze umane si ricollega alla teoria che
esponiamo in questa opera. ...
Tutti gli
avvenimenti, anche quelli che per la loro piccolezza sembrano non ubbidire alle
grandi leggi della natura, ne sono una conseguenza necessaria come lo sono le
rivoluzioni del Sole. Ignorando il
legame che li uniscono al sistema intero dell’universo, li si è fatti dipendere
dalle cause finali o dal caso, a seconda che si manifestassero e si
succedessero con regolarità o senza ordine apparente; ma queste cause
immaginarie sono state successivamente arretrate sino ai limiti delle nostre
conoscenze e spariscono del tutto davanti alla sana filosofia la quale non vede
in esse che l’espressione dell’ignoranza in cui ci troviamo circa le vere cause.
Gli
avvenimenti attuali hanno coi precedenti un legame fondato sul principio
evidente che nulla può cominciare ad essere senza una causa che lo produca.
Quest’assioma, noto sotto il nome di principio della ragion sufficiente, si
estende anche alle azioni che giudichiamo indifferenti. Neppure la volontà più
libera può dar loro nascita senza un motivo determinante; giacché, se essa
stimando perfettamente simili le circostanze di due posizioni, agisse in una e si astenesse dall’agire nell’altra, opererebbe una scelta che sarebbe
un effetto senza causa; che
sarebbe insomma, dice Leibniz, il caso
cieco degli epicurei. Ma l’opinione contraria alla nostra è un’illusione
dello spirito che, perdendo di vista le ragioni fugaci della scelta della
volontà nelle cose indifferenti,
si persuade che essa si determini da se e senza motivo.
Dobbiamo
dunque considerare lo stato presente dell’universo come l’effetto del suo stato
anteriore e come la causa del suo stato futuro. Un’Intelligenza che, per un
dato istante, conoscesse tutte le forze da cui è animata la natura e la
situazione rispettiva degli esseri che la compongono, se per di più fosse
abbastanza profonda per sottomettere questi dati all’analisi, abbraccerebbe
nella stessa formula i movimenti dei più grandi corpi dell’universo e
dell’atomo più leggero: nulla sarebbe incerto per essa e l’avvenire, come il
passato, sarebbe presente ai suoi occhi. Lo spirito umano offre, nella
perfezione che ha saputo dare all’astronomia, un pallido esempio di quest’Intelligenza. Le sue
scoperte in meccanica e in geometria,
unite a quella della gravitazione universale, l’hanno messo in grado di
abbracciare nelle stesse espressioni analitiche gli stati passati e quelli
futuri del sistema del mondo.
Applicando lo
stesso metodo ad altri oggetti delle sue conoscenze, è riuscito a ricondurre a
leggi generali i fenomeni osservati e a
prevedere quelli che devono scaturire da circostanze date. Tutti i suoi sforzi
nella ricerca della verità tendono ad avvicinarlo continuamente
all’Intelligenza che abbiamo immaginato, ma da cui resterà sempre infinitamente
lontano. Questo tendere, che è proprio della specie umana, è ciò che ci rende
superiori agli animali, ed i progressi nel campo della scienza distinguono le
nazioni ed i secoli e rappresentano
la loro vera gloria....
... La
regolarità, che l’astronomia ci presenta nel movimento delle comete, ha luogo,
senza dubbio, in tutti i fenomeni. La curva descritta da una semplice molecola
di aria o di vapore è regolata con la stessa certezza delle orbite planetarie:
non v’è tra di esse nessuna differenza, se non quella che vi pone la nostra ignoranza.
La probabilità
è relativa in parte a questa ignoranza, in parte alle nostre conoscenze....
La teoria dei
casi consiste nel ridurre tutti gli eventi dello stesso genere ad un certo
numero di casi ugualmente possibili, cioè tali da renderci indecisi circa la
loro esistenza, e nel determinare il numero dei casi favorevoli all’evento di
cui si ricerca la probabilità. Il rapporto tra questo numero e quello di tutti
i casi possibili è la misura della probabilità, la quale perciò non è che una
frazione, il cui numeratore è il numero dei casi favorevoli e il cui
denominatore è il numero di tutti i casi possibili... …Dobbiamo
essere indulgenti nei riguardi delle opinioni diverse dalle nostre, perché la
differenza spesso dipende solo dai punti di vista diversi in cui ci hanno posti
le circostanze. Portiamo i nostri lumi a coloro che giudichiamo
insufficientemente istruiti; ma prima esaminiamo severamente le nostre opinioni
e misuriamone con imparzialità le probabilità rispettive.
La differenza
di opinione dipende anche dal modo con cui si determina l’influenza dei dati
che sono noti. La teoria delle probabilità affronta delle questioni così
sottili, che non è per niente sorprendente se due persone giungono a risultati
diversi, soprattutto in problemi molto delicati, pur avendo gli stessi dati.
Esponiamo ora i principi generali di questa teoria”.
Quindi, per Laplace, “quasi tulle le nostre conoscenze non sono che probabili”;
ma, invece, “tutti gli avvenimenti
sono una conseguenza necessaria delle grandi leggi della natura”;
per cui di ognuno dobbiamo ricercarne le cause che necessariamente esistono
per il “principio della ragion sufficiente”.
L’“ignoranza” delle cause porta gli uomini a fare dipendere gli avvenimenti “dalle cause finali o dal caso”,
ma “il caso cieco degli epicurei” non
esiste; esistono, invece, i casi,
termine sinonimo di situazioni
possibili ma ignote, per cui l’uomo deve dirigere “tutti i suoi sforzi nella ricerca della
verità”, per “avvicinarsi
continuamente all’Intelligenza che abbiamo immaginato, ma da cui resterà
sempre infinitamente lontano”; e questo nonostante sappiamo che “la curva descritta da una semplice molecola
di aria o di vapore è regolata con la stessa certezza delle orbite planetarie” e
che “non v’è tra di esse nessuna
differenza, se non quella che vi pone la nostra ignoranza”.
Questa può essere ridotta, ma mai eliminata;
per cui “la probabilità è relativa in
parte a questa ignoranza, in parte alle nostre conoscenze”.
Quale metodo propone Laplace a questo scopo?
Quello di “ridurre
tutti gli eventi dello stesso genere ad un certo numero di casi ugualmente
possibili, cioè tali da renderci indecisi circa la loro esistenza, e nel
determinare il rapporto tra il namero dei casi favorevoli all’evento di cui si
ricerca la probabilità e il numero di tutti i casi possibili”.
In questa definizione vediamo un elemento “soggettivo” relativo allo stato della
nostra conoscenza che non ci permette, arrivati a un certo punto dell’analisi,
di giudicare se un caso elementare sia più o meno probabile di un altro caso
elementare, perché non vi sono più, a nostra conoscenza, “ragioni sufficienti” per privilegiarne alcuno. Ma vi è anche un
forte elemento “oggettivo” legato
alla convinzione che il sistema del mondo funzioni come un orologio, tanto che
un’ipotetica Intelligenza sarebbe in grado di conoscere passato, presente e
futuro, purché in possesso delle informazioni sufficienti.
Questa definizione è stata (e lo è ancora)
assoggettata a varie speculazioni filosofiche, alcune tendenti a
sopravvalutarne l’aspetto “soggettivo”,
altre quello “oggettivo”;
molti si sono chiesti se la misura della probabilità deve stimarsi “a priori” o “a posteriori”, allo scopo di superare l’apparente circolarità
della definizione. Ma il significato di tali termini (soggettivo, oggettivo, a
priori, a posteriori) è stato ed è molto vago, tanto che i vari autori ne fanno
usi che differiscono tra loro in modo financo contraddittorio.
Sulla circolarità della definizione è
interessante leggere un breve articolo di Peano a tale proposito.9
“La
definizione comunemente adottata è “la probabilità di un avvenimento è il
rapporto del numero dei casi favorevoli all’avvenimento, ai numero dei casi
possibili”, e si suole aggiungere, o subito, o dopo una pagina,“a condizione
che questi ultimi siano egualmente possibili”.
Invece di
dire, col Bertrand, che i casi si suppongono egualmente possibili, dicono
alcuni, col Poincaré, che i casi sono egualmente verosimili, o col Borel,
egualmente probabili.
Questa definizione,
che definisce la probabilità mediante il probabile, contiene un circolo
vizioso evidente. Il circolo vizioso è maestoso, ma rimane, se al posto di
probabile usiamo un sinonimo: possibile o verosimile; poiché al posto di
probabilità potremmo dire possibilità o verosimiglianza.
Il circolo
vizioso è riconosciuto da parecchi autori. Il Poincaré dice:
“La définition complète de la probabilité est donc une
sorte de pétition de principe. Une définition mathématique ici n’est pas
possible”. E il Borel dice: “Cette
définition complète renferme en apparence un cercle vicieux”, e afferma
impossibile il dare una definizione di probabilità senza servirci del
linguaggio ordinario.
Io mi
propongo di dimostrare che è possibile la definizione simbolica di probabilità,
cioè che si può formare un’eguaglianza il cui primo membro è la probabilità che
si vuole definire, ed il secondo membro è un gruppo di simboli precedentemente
definiti, seguendo il mio Formulano Mathematico, editio V.
a,b Î Cls . Num
a Î N1. É . P(b,a) = Num(a ∩ b) / Numa
che letteralmente si legge:
“Se a e b sono classi, e il
numero degli individui della classe a è finito, allora il nuovo simbolo P(b, a)
vale il numero degli a che sono b, diviso pel numero totale degli a”.
Accostandoci
alla definizione comune, possiamo leggere la definizione simbolica come segue:
“Se a è la classe dei casi possibili, che si suppongono in numero finito, e b è
la classe dei casi favorevoli, col simbolo P(b, a), che si legge: probabilità
dell’avvenimento b fra gli avvenimenti a, si intende il rapporto fra il numero
dei casi possibili, che sono favorevoli, al numero totale dei casi possibili”.
I simboli
matematici sono spesso suscettibili di più interpretazioni. La definizione
simbolica che precede, si può anche leggere:
“Se a è una
lega, b è il metallo fino, o oro, allora P(b, a), che conviene di leggere:
titolo della lega, si intende il rapporto fra il numero dei grammi d’oro che
sonvi nella lega, al peso totale della lega”.
I teoremi
fondamentali sulle probabilità assumono forma semplicissima come pure le loro
dimostrazioni.
…
Il simbolo
P(b, a) che si definisce, è funzione di due classi di variabili a e b. È
lecito leggerlo: “probabilità dell’avvenimento d’un caso b fra i casi a” ovvero
“percentuale dei b fra gli a”, o altrimenti, purché sempre si enuncino le due
variabili a e b.
La frase
comune “probabilità d’un avvenimento”, si presenta come una funzione di una
sola variabile, dell’avvenimento; e dato l’avvenimento, non risultano
determinate le classi dei casi possibili e favorevoli.
La questione
“qual è la probabilità che domani piova” non ha senso, perché non sono
enunciate le due classi a e b da cui dipende la probabilità. Vi si può
rispondere completando la frase ellittica, per esempio così: “la pluviosità in
questo mese, o stagione, o in tutto l’anno, cioè il rapporto fra il numero dei
giorni di pioggia e il numero totale dei giorni nel mese, o stagione, o anno,
è tanta”.
La frase
“probabilità di un avvenimento” è una frase incompleta; e considerandola come
completa, assoluta, si incontrano le difficoltà; basta completarla,
coll’enunciare le due classi variabili, per eliminare ogni difficoltà. È una
frase simile alle:
il punto a è
fisso (senza dire rispetto a chi);
il numero a è
costante (senza dire chi varia), ecc.”
Quindi, secondo Peano, a parte le ovvie
precisazioni che fa sull’incompletezza delle frasi comunemente usate, la
probabilità è un numero determinabile “oggettivamente”,
una volta assegnate (questa volta “soggettivamente”,
o per convenzione “intensoggettiva”)
le classi finite da cui dipende, o, eventualmente, le due grandezze
fisiche delle quali ne è il rapporto (o titolo, per l’orefice), è irrilevante,
per tale definizione, l’uso che ognuno ne vorrà fare e non ha nessuna
caratterizzazione di “attesa” o “aspettazione” per un qualche
avvenimento futuro. Anche se niente impedisce che la si possa usare anche in
questo senso per “comportamenti
razionali”, per usare la terminologia degli
strateghi moderni, specialisti della teoria dei giochi e della programmazione
(lineare o non).
Dalle precedenti citazione emerge che, anche
se non è possibile assegnare un numero al “caso”, è tuttavia possibile
assegnare un numero a una sottoclasse di “casi”, che si chiama “probabilità”.
Tuttavia, anche se la “probabilità”, che come
ci ricorda Laplace è legata alla nostra conoscenza e alla nostra ignoranza, è
misurabile non ha ancora l’aspetto di una grandezza additiva in relazione alla
nostra ignoranza. Boltzmann ha trovato il modo di introdurre una particolare
funzione della probabilità che si presta ottimamente a calcolare
quantitativamente l’informazione che ci manca per conoscere completamente
tutti i dettagli di una data situazione.
Oggi si arriva alla definizione di Boltzmann
in modo più generale entro quella che si chiama “teoria dell’informazione”.
Sotto il nome di “teoria dell’informazione” oggi si intende una ben determinata
teoria matematica strettamente connessa alla teoria delle probabilità. Il
collegamento tra probabilità e conoscenza è molto antico ed è la ragione delle
interpretazioni soggettivistiche del concetto di probabilità; abbiamo visto,
nelle citazioni di Laplace sopra riportate, come lo stesso Laplace, pur avendo
dato una definizione oggettiva di probabilità, per illustrarne gli usi facesse
appello a termini quali conoscenza e ignoranza. In passato alcuni studiosi di
problemi statistici hanno fatto uso del termine informazione per una grandezza, oggettivamente definita, legata
alla varianza di una distribuzione di probabilità.
La definizione matematica moderna di informazione coincide, formalmente, con
la definizione microscopica di entropia come
data da Boltzmann.
Più recentemente, simili definizioni sono
state date da Nyquist (1924), Hartley (1928) e altri, in connessione con la
trasmissione di segnali elettrici su un canale di comunicazione telefonico o
telegrafico.
Tuttavia la teoria, come oggi adoperata, si
fa risalire a un famoso lavoro di Shannon (1948) dove si affronta il problema
della misura della quantità di informazione trasferibile attraverso un canale
di comunicazione, astrattamente definito, in presenza di rumore di fondo.
Proprio l’impostazione astratta del problema
dà alla teoria la massima generalità e permette di applicarla in moltissime
situazioni, anche lontanissime dal campo specifico in cui è stata introdotta.
Si può dire che la teoria può essere
applicata in tutti i campi in cui si applica la teoria delle probabilità e lo
stesso problema può essere affrontato con entrambi i linguaggi. Tuttavia, l’uso
di un linguaggio piuttosto che di un altro, in determinate situazioni, può
avere maggiore potenza euristica, a parte le semplificazioni formali che l’uno
o l’altro linguaggio possono introdurre nelle specifiche situazioni. In
generale, anche se due linguaggi diversi sono interamente traducibili tra
loro, difficilmente possono risultare completamente equivalenti ai fini della
loro utilizzazione pratica, nei diversi contesti.
Per quanto riguarda le possibili
interpretazioni del concetto di informazione notiamo che, data la stretta
relazione con il concetto di probabilità, è ovvio che ce ne sono di quelle che
si ispirano al soggettivismo più esasperato e di quelle che fanno riferimento
all’oggettivismo più intransigente.
Per chiarire l’essenza della definizione,
consideriamo un semplice problema di scelta casuale.
Ci vengono presentate n scatole, in una di esse è stato nascosto un oggetto, le altre
sono vuote.
In questo caso, gli n eventi, definiti dalla proposizione:
“l’oggetto si trova
nella scatola i-esima” (i = 1,...,n) ,
sono mutuamente esclusivi ed esaustivi, cioè formano un insieme statistico completo (in una delle scatole e solo in una vi è sicuramente l’oggetto cercato).
A priori assumeremo che tutte le n possibilità siano equiprobabili.
La nostra “ignoranza”
sulla scatola che contiene l’oggetto potrebbe essere ridotta effettuando
alcune prove empiriche (p. es. scoperchiando qualche scatola) o per effetto di
qualche “informazione” supplementare
che ci potrebbe fornire chi ha preparato le scatole (p. es. ci potrebbe
informare che le ultime due scatole sono vuote).
In assenza di tali informazioni ci proponiamo
di definire una conveniente misura per la quantità di “informazione mancante”, che è necessaria per colmare la nostra ignoranza.
Ovviamente essa può dipendere solo dal numero
n (escludendo che la forma delle scatole o la natura dell’oggetto
possano avere alcuna influenza sulla probabilità di individuare la scatola che
contiene l’oggetto dato ed escludendo, ovviamente, la possibilità di capacità
telepatiche, ammesso che possano esistere); se il numero delle scatole fosse
maggiore, ovviamente, risulterebbe più difficile trovare l’oggetto; al
contrario, se n = 1, non avremmo
bisogno di alcuna altra informazione. Quindi possiamo pretendere che si abbia:
( I l ) I (1) = 0
Cioè è nulla l’“informazione mancante”.
Per n finito,
basterà un numero finito di prove per sapere dove si trova l’oggetto. Se n cresce, allora il numero delle prove
necessarie crescerà e possiamo supporre che l’informazione mancante sia, in tal
caso, maggiore, cioe, si debba avere:
( I 2 ) se (n >
m) allora I (n) > I (m).
Possiamo immaginare una situazione più
complicata in cui le n scatole
contengano, ognuna, m comparti e
l’oggetto è nascosto in uno di questi comparti.
Il numero di possibilità totali è, ora, N = n m .
Se vogliamo che la I si comporti come una “quantità”, dobbiamo pretendere che sia
additiva per i due eventi indipendenti che l’oggetto si trovi nel comparto i della scatola j, per cui:
( I 3 ) I (N) = I (nm) =
I (n) + I (m).
Possiamo scrivere la ( I 3
) anche nella forma:
I (N) = I (n) + I (N / n) ,
da cui:
I (N
/ n) = I (N) - I (n) .
Mediante quest’ultima, si può estendere la
definizione anche al caso che N / n non sia un numero intero e, con un processo al limite, anche a
qualunque numero reale:
( I 4 ) ![]()
con ![]() , numero reale, e an una successione opportuna di numeri razionali.
, numero reale, e an una successione opportuna di numeri razionali.
Quindi la ( I 3
) si può scrivere, per qualunque coppia di numeri reali x e y,
nella forma:
( I 5 ) I (x y) =
I (x) + I (y).
Le proprietà richieste dalle ( I 1 ), ( I 2
), ( I
5 )definiscono univocamente
la relazione che deve esistere tra I e
x.
Infatti si può dimostrare che l’unica
funzione continua, I (x), che
soddisfi la (5), può essere solo la:
I (x) = k ln x
e, quindi, possiamo definire l’informazione mancante con la:
( I 6 ) I (n) = k
ln n = - k ln 1/n = - k ln p
Essendo p = 1/n la probabilità di scegliere la scatola giusta al primo tentativo.
La costante k può dipendere solo dalla scelta dell’unità di misura, quindi è
una costante universale.
Possiamo applicare la definizione precedente
anche alla seguente situazione:
Si abbia una macchina da scrivere capace di
stampare 75 caratteri distinti, compreso lo spazio bianco (per non complicare
inutilmente le cose, supporremo di non avere a disposizione il tasto per
cambiare riga e che il cambio avvenga automaticamente alla fine del rigo di una
pagina standardizzata sia in lunghezza che in larghezza).
I fogli di carta in nostro possesso siano
tutti uguali tra loro e supponiamo che possano contenere, esattamente, N caratteri (sempre contando lo spazio
bianco come un carattere, alla stessa stregua degli altri, quindi, anche una
pagina interamente bianca è da considerare uno dei possibili messaggi).
Quanti messaggi diversi (cioè distinguibili
per almeno un carattere diverso), di una sola pagina, possiamo scrivere?
Ovviamente: 75N (cioè,
il numero delle disposizioni con ripetizione di 75 elementi di classe N).
Trascurando correlazioni linguistiche,
l’informazione contenuta in una pagina del tipo sopradescritto, sarà:
( I 7 ) I = k ln 75N
= N k ln 75 =
N I1 ,
avendo indicato con I1 = k ln 75 la quantità
di informazione da attribuire al singolo carattere.
Naturalmente anche una pagina scritta da uno
scimpanzè deve considerarsi “informazione”, secondo la definizione che abbiamo
dato!
Se fossimo in possesso di qualche
informazione suppletiva l’informazione mancante (cioè la nostra ignoranza)
relativa ad una pagina diminuirebbe, come è ovvio.
Per esempio, provate a leggere:
LEG E DI NEW
N.
Se sappiamo trattarsi di una pagina di fisica
non è necessario, in generale, riuscire a leggere tutti i caratteri. La ragione
è che vi sono determinate correlazioni tra i singoli caratteri o tra le parole,
almeno tra caratteri che si trovino vicini nella pagina.
La probabilità con la quale compaiono i
singoli caratteri è definita nei singoli contesti (per esempio, pagina scritta
in lingua italiana, testo di fisica, ecc.).
Se conosciamo le singole frequenze possiamo
calcolare l’informazione media per carattere contenuta in una pagina, pesando
opportunamente l’informazione per carattere con le frequenze empiricamente
misurate:
![]() ,
,
(![]() e
e ![]() ).
).
Ponendo ![]() , scriveremo:
, scriveremo:
( I 8 ) ![]() ,
,
(il segno meno rende positiva l’informazione mancante, per cui l’informazione acquisita sarà di segno negativo; con
questo si viene ad identificare l’informazione mancante con l’entropia. Da ora
in poi non sarà più necessario usare gli aggettivi mancante o acquisita perché
il segno del valore della quantità ci dirà di che si tratta).
Si assume usualmente la ( I 8 ), come definizione di
informazione, che è più generale della (
I 6 ), come definizione di informazione
(entropia).
Ma facilmente si può ricondurre la ( I 8 ) alla definizione ( I 6 ).
Poniamoci ora il problema di stabilire
un’opportuna unità di misura per l’informazione o, in altre parole, di
assegnare un valore ed un’opportuna dimensione fisica alla costante k. A tale scopo, consideriamo una
successione di lanci di una singola moneta, o una qualunque situazione con “codificazione binaria”: testa-croce,
punto-linea (come nell’alfabeto morse), chiuso-aperto (come nei circuiti
elettrici), ecc.
In tal caso si ha n = 2. Per N lanci
(ovvero per una “parola” di N caratteri binari, cioè di N bit — bi[nary digi]t —) il
numero di possibilità diverse sarà R =
2N e, quindi:
I = k ln 2N = N k ln 2 ;
se scegliamo ![]() si avrà:
si avrà:
I = N bit
.
Ovvero, cambiando la base dei logaritmi:
I = log2 R
= log2 2N =
N
.
Ricordiamo ora che, secondo la relazione di
Boltzmann, l’entropia è
S = k ln W ,
con k la costante di
Boltzmann e W il numero delle
possibili configurazioni (nello spazio delle fasi) del sistema fisico
considerato (“complessioni”); quindi, a meno di
una costante universale, l’entropia risulta proporzionale all’informazione
mancante (si può dire che l’entropia non è altro che una misura della nostra “ignoranza” sulle condizioni del sistema
fisico!).
Volendo, si possono dare dimensioni fisiche
di entropia all’informazione, scegliendo:
k = 1.38 ´ 10-16 erg/°K.
Ovviamente sarà:
1 bit = k
ln 2 » 10-16 erg/°K .
Sorge il problema di capire come mai un
concetto, quale l’informazione, definito finora a livello logico e puramente
astratto, possa avere connessioni con una proprietà fisica di un sistema fisico
concreto.
La discussione su questo punto è stata sempre
aperta. Per il momento descriviamo la soluzione più accreditata di tale
problema, così come proposta da Brillouin,10
il quale ricorre alla distinzione tra i concetti di “informazione libera” e di
“informazione vincolata”.
Si parla di “informazione libera” quando essa viene pensata in astratto in connessione
con le diverse possibilità logiche in cui possiamo distinguere un sistema di
segni.
Si parla, invece, di “informazione vincolata” quando la stessa informazione viene “implementata” in un sistema fisico, sia
esso costituito da una lettera (epistolare) scritta con l’inchiostro su di un
foglio di carta, o su di un nastro perforato o magnetico, o l’informazione
fisica contenuta nel gas di un recipiente, o qualsiasi altro sistema capace di
trasportare o memorizzare informazione.
Alcuni pensano che l’informazione libera può
solo pensarsi come necessariamente vincolata, se non altro ai neuroni del
cervello. Ma qui entriamo in un campo dove non è mai stato chiaro il ruolo
relativo di fisica e filosofia.
Dal punto di vista della fisica la soluzione
di tale problema può risultare irrilevante, se ci limitiamo solo allo studio di
un sistema fisico concreto e se intendiamo per “informazione” solo quella massima che il sistema può contenere,
per cui avremo un’identificazione totale tra il concetto di informazione
mancante e quello di entropia.
In tal modo, una variazione di informazione,
in quanto necessariamente vincolata, si può avere se e solo se si verifica una
corrispondente variazione nel numero delle complessioni del sistema fisico e,
quindi, solo se si ha una variazione di entropia.
In ogni caso, come già osservato
precedentemente, il valore semantico o utilitario dell’informazione è del tutto
estraneo alla definizione (I 8); e ciò indipendentemente dal
fatto che essa sia libera o vincolata. Il dattiloscritto di uno scimpanzè ha lo
stesso contenuto di informazione di una pagina di fisica.
Del resto, quando l’ingegnere progetta un
canale di comunicazione (p. es. il telefono) non si preoccupa di sapere se sarà
usato per chiacchiere inutili o per urgenti e importanti comunicazioni, il cui
valore semantico e, eventualmente, utilitario deriva da necessità biologiche o
da convenzioni sociali.
La definizione (I 8) dà,
quindi, una quantità che è legata univocamente ad una determinata distribuzione
di probabilità e può essere usata in due modi diversi:
(i) se
la distribuzione (cioè i valori delle pi) è nota, allora la (I
8) ci permette di calcolare I;
(ii) la (I 8) può anche
essere usata come relazione funzionale tra la I e le pi .
Facciamo un esempio relativo al secondo modo
di usare la (I 8):
Consideriamo un insieme statistico di
contenitori, contenenti ciascuno N molecole
di gas.
Supponiamo che la distribuzione in ciascun
contenitore sia diversa e indichiamo con pi la probabilità che
una molecola si trovi nella celletta i-esima dello spazio delle fasi
opportunamente suddiviso [1 £ i £ n].
Se le distribuzioni sono puramente casuali ha
senso chiedersi qual è la distribuzione più probabile, cioè quella che si può
realizzare in un maggior numero di modi (possibilità). Secondo la (I 8)
tale distribuzione si ottiene per I massima.
Il problema si riduce a trovare la
distribuzione, cioè i valori delle pi, che massimizzano I sotto il vincolo (cioè con
l’informazione suppletiva in nostro possesso) che:
![]()
Il problema, così posto, si risolve
facilmente mediante il metodo dei moltiplicatori di Lagrange:
![]() = massimo
= massimo
cioe
![]() per ogni j ;
per ogni j ;
da cui
![]() ,
,
si trova che le pj sono, in questo caso, indipendenti
dall’indice j.
Per determinare λ ricorriamo all’equazione del vincolo:
![]() ,
,
da cui
![]() ,
, ![]() ,
, ![]()
La distribuzione più probabile, in questo
caso, risulta essere quella equiprobabile.
Ma supponiamo ora di possedere altra
informazione, ad esempio, sappiamo che in un dato volume di gas non si abbiano
forze esterne, per cui il moto del baricentro è costante ed eguale a xB .
Per semplicità immaginiamo un ipotetico gas
unidimensionale con molecole tutte di egual massa. La coordinata del
baricentro sarà:
![]() .
.
Poiché la distribuzione degli impulsi non
viene modificata da questo vincolo possiamo limitarci allo spazio delle
configurazioni; l’indice i,
in questo caso, indicherà un segmento sulla retta reale.
Analogamente, se avessimo solo l’informazione
che le perdite per radiazione sono trascurabili, anche perché la distanza
media tra le molecole è molto grande e quindi sono trascurabili anche le
interazioni tra le molecole (gas perfetto) dobbiamo, invece, imporre il
vincolo:
![]()
In quest’ultimo caso ci possiamo limitare
allo spazio degli impulsi e la celletta i
indicherà un volumetto in questo spazio.
Massimizzando la I, considerata come funzione delle pi ,
tenuto conto dei vincoli, cioè dell’informazione suppletiva in nostro possesso
è possibile trovare la distribuzione che massimizza la I.
Del resto questo è il modo che usò Boltzmann
per le sue brillanti scoperte nel campo della meccanica statistica e della
teoria cinetica dei gas.
Ma si possono facilmente sviluppare le
formule nel caso più generale in cui si abbiano M relazioni del tipo
![]() [α = 1, 2, …, M] ,
[α = 1, 2, …, M] ,
con l’ulteriore condizione ![]() .
.
L’entropia, in tal caso, è:
![]()
I metodi con i quali si arriva a quest’ultima
formula permettono in modo del tutto generale di determinare, non solo la
quantità di informazione mancante (cioè la rimanente ignoranza) sul fenomeno
in studio dopo avere incluso nel processo di massimizzazione la nostra attuale
conoscenza, ma anche la nuova distribuzione di probabilità da impiegare per le
indagini successive.
Stabilito il metodo, la matematica ci
permette di asserire che, quando due sistemi di conoscenze si fanno interagire,
il risultato è sempre un aumento della nostra ignoranza.
Questo è il significato ultimo della seconda
legge della termodinamica, il principio universale dell’aumento dell’entropia
nei sistemi isolati.
Infatti, si dimostra che, se si considerano
due sistemi inizialmente separati (cioè, meccanicamente isolati, e quindi
isolati anche termodinamicamente), con energie totali, U1 e U2
rispettivamente, se tali due sistemi vengono in qualche modo in
contatto tra loro, in modo che si possano esercitare degli scambi reciproci di
energia, e poi i due sistemi vengano nuovamente separati, il risultato sarà una
perdita di informazione sui valori U1′ e U2′ delle energie finali dei due sistemi,
nonostante il principio di conservazione dell’energia imponga che la loro somma
resti la stessa di prima: U1 + U2
= U1′ + U2′ .
Questo comporta un aumento irreversibile dell’entropia
e quindi una diminuizione irreversibile della quantità di energia utilizzabile.
Ma, per capire meglio la reciproca relazione
tra entropia, informazione, ordine e irreversibilità, notiamo che le formule
sopra derivate valgono anche nel caso unidimensionale e anche per una sola
particella. In tal caso si ha che la variazione di entropia per un sistema
costituito da una sola particella che vada avanti e indietro, lungo un percorso
lineare di data lunghezza, con velocità costante in modulo, è ΔS = k ln 2, quando si raddoppi la lunghezza del percorso lineare.
Sia l la lunghezza del percorso e λ la dimensione lineare della
particella; se ![]() allora la probabilità
di trovare la particella in un certo punto del percorso sara circa
allora la probabilità
di trovare la particella in un certo punto del percorso sara circa ![]() ; e, quando si raddoppi il percorso, sara circa
; e, quando si raddoppi il percorso, sara circa ![]() .
.
L’informazione mancante sarà proporzionale
a ![]() nel primo caso, e
proporzionale a
nel primo caso, e
proporzionale a ![]() (maggiore della
prima), nel secondo caso. Ma il rapporto tra le probabilità e,
conseguentemente, la differenza di informazione è oggettivamente data,
indipendentemente dal fatto che la nostra informazione soggettiva sia nulla o
totale, essa dipende solamente dal maggiore o minore spazio che la particella
ha a disposizione (che comporta pure una maggiore o minore pressione esercitata
impulsivamente agli estremi del percorso, cioè verso l’esterno, anche nel caso
che il volume a disposizione delle particelle sia limitato al prodotto di l per la sezione d’urto delle
particelle, per il fatto che la pressione verso l’esterno si dimezza in ogni
caso per aver tolto le due facce del setto divisorio che comunica le variazioni
di impulso all’esterno).
(maggiore della
prima), nel secondo caso. Ma il rapporto tra le probabilità e,
conseguentemente, la differenza di informazione è oggettivamente data,
indipendentemente dal fatto che la nostra informazione soggettiva sia nulla o
totale, essa dipende solamente dal maggiore o minore spazio che la particella
ha a disposizione (che comporta pure una maggiore o minore pressione esercitata
impulsivamente agli estremi del percorso, cioè verso l’esterno, anche nel caso
che il volume a disposizione delle particelle sia limitato al prodotto di l per la sezione d’urto delle
particelle, per il fatto che la pressione verso l’esterno si dimezza in ogni
caso per aver tolto le due facce del setto divisorio che comunica le variazioni
di impulso all’esterno).
Quindi l’entropia ha certamente a che fare
con l’informazione e con la probabilità, ma solo in quanto, oggettivamente e
fisicamente, misurabile; l’informazione dovuta al colore delle particelle,
anche se oggettivamente determinabile, non ha niente a che fare con
l’entropia.
Ma prima notiamo, anche, che l’entropia così
definita non ha a che fare nemmeno con la nozione di disordine molecolare. Il
moto di una sola particella nelle condizioni date, è perfettamente ordinato,
ciononostante si verificano variazioni di entropia specifica nella stessa
misura di un sistema di molte particelle con moto comunque disordinato.
Tuttavia la nozione di disordine e quella di
informazione soggettiva sono connesse all’irreversibilità del fenomeno.
Nel caso monoparticellare e monodimensionale
di cui sopra, immaginiamo che la variazione della lunghezza del percorso venga
effettuata per l’interposizione di un setto divisorio che impedisca il
proseguimento del moto della particella nel verso di percorrenza e la
costringa ad invertire il moto senza, però, cambiarne il modulo della velocità.
Se noi conosciamo la fase iniziale del moto
possiamo ripristinare, inserendo al momento opportuno il setto divisorio,
l’informazione che abbiamo perduto quando lo si è tolto. Ma se non conosciamo
la fase iniziale avremo solo una probabilità uguale ad ![]() (nel caso di setto
posto a metà percorso) di ripristinare la situazione ad entropia minore. Nel
caso di molte particelle con velocità distribuite secondo la distribuzione di
Maxwell - Boltzmann (corrispondente al massimo della probabilità), anche se
accettassimo il risultato del teorema di Poincaré, la probabilità di
ristabilire la situazione iniziale diventa piccolissima; e, date le difficoltà
di calcolo, specialmente se le molecole interagiscono, anche se debolmente, il
ripristinare la situazione iniziale risulta, in pratica, impossibile anche nel
caso che noi potessimo conoscere tutte le fasi iniziali. In quest’ultimo caso,
la nostra conoscenza soggettiva si traduce in ignoranza oggettiva, cioè in
entropia, a causa del disordine molecolare di Boltzmann.
(nel caso di setto
posto a metà percorso) di ripristinare la situazione ad entropia minore. Nel
caso di molte particelle con velocità distribuite secondo la distribuzione di
Maxwell - Boltzmann (corrispondente al massimo della probabilità), anche se
accettassimo il risultato del teorema di Poincaré, la probabilità di
ristabilire la situazione iniziale diventa piccolissima; e, date le difficoltà
di calcolo, specialmente se le molecole interagiscono, anche se debolmente, il
ripristinare la situazione iniziale risulta, in pratica, impossibile anche nel
caso che noi potessimo conoscere tutte le fasi iniziali. In quest’ultimo caso,
la nostra conoscenza soggettiva si traduce in ignoranza oggettiva, cioè in
entropia, a causa del disordine molecolare di Boltzmann.
Riesaminiamo il sistema di oscillatori
accoppiati che abbiamo discusso precedentemente dal punto di vista delle
variazioni di informazione.
L’energia, che per le ipotesi del modello è
all’istante iniziale solo cinetica e tutta concentrata sul primo oscillatore,
con l’andare del tempo si propaga lungo il sistema e si divide in parte in
energia cinetica dei singoli oscillatori e in parte in energia potenziale di
interazione mutua tra oscillatori, che sarebbe arbitrario attribuire a questo o
a quell’altro oscillatore ma riguarda tutto il sistema (la potremmo chiamare
“energia di campo”).
A causa della relazione sinusoidale tra ωj e
j, il sistema assume
caratteristiche fortemente dispersive, per cui l’impulso iniziale viene con
l’andare del tempo ad allargarsi considerevolmente, fino a raggiungere una
situazione, che possiamo chiamare di equilibrio statistico o termodinamico, in
cui tutti gli oscillatori vibrano contemporaneamente con la stessa energia
media ma con amplissime fiuttuazioni statistiche.
L’analisi matematica del modello ci dice che
l’ampiezza dei singoli modi normali è costante nel tempo, in quanto fissata
dalle particolari condizioni iniziali imposte al sistema, il quale è
perfettamente deterministico, anche se appare assolutamente casuale nelle
variabili che abbiamo scelto di graficare, che danno l’apparenza di un
comportamento termodinamico che, a lungo andare, fa perdere l’informazione
iniziale, secondo la quale l’energia era concentrata sulla prima particella
della catena.
Quindi l’informazione che avevamo all’inizio
sull’energia cinetica del sistema (tutta concentrata sulla prima particella) si
va degradando irreversibilmente fino a raggiungere il suo valore massimo, che
corrisponde all’entropia d’equilibrio del sistema.
Questo semplice esempio meccanico è il
paradigma del degrado continuo dell’informazione che noi possiamo avere anche
su un sistema perfettamente deterministico e quindi anche della continua
diminuzione della nostra capacità di sfruttare al massimo, ai nostri fini,
l’eventuale conoscenza che noi avessimo in un determinato istante
sull’andamento di un qualsiasi processo.
Con tale paradigma vediamo cosa possiamo
dedurre sulle conseguenze dell’impatto del sistema economico sull’ambiente.
A differenza del modello degli oscillatori,
in cui tutto è noto e quindi perfettamente deterministico, qui quasi niente è
noto e un qualsiasi modello che possiamo costruire deve essere necessariamente
indeterministico, peggiorando così le nostre possibilità di sfruttamento di
eventuali conoscenze.
Ma anche se facessimo l’ipotesi assurda di
conoscere tutte le leggi del sistema e tutte le condizioni iniziali, come
l’ipotetica Intelligenza di Laplace, la continua interazione del sistema
economico sull’ambiente non farebbe altro che peggiorare continuamente la
nostra “informazione” sul sistema ambiente.
Fino al raggiungimento dell’entropia massima,
che non siamo in grado di stimare.
Naturalmente in questo percorso incontreremo
prima la fine della vita del nostro ecosistema, ma su questo rimandiamo
all’articolo di Pagano in questo numero di Mondotre/Quaderni e a un nostro
precedente libro.11
NOTE
1 D.E. James et al., Economic Approaches to Environmental Problems, Elsevier, Amsterdam,
1978. TORNA
2 Cfr. N.
Georgescu-Roegen, The entropy law, and
the economic process, Harvard, 1971. TORNA
3 Cfr. L.
Boltzmann, Theoretical Physics and
Philosophical Problems, Reidel, Boston, 1974. TORNA
4 ibidem, p. 96. TORNA
5 Notiamo che questo particolare orologio che abbiamo escogitato non ha niente a che vedere con quelli usualmente chiamati “orologi atomici” che sono basati su processi più deterministici. TORNA
6 I.
Prigogine, Tempo, irreversibiliià e
struttura, in La nuova alleanza, Longanesi,
1981. TORNA
7 Cfr. L.
Landau, E. Lifshitz, The classical theory
of fields, Addison - Wesley, 1951, p. 1 e segg. TORNA
8 Opere di Pierre Simon Laplace, UTET, 1967, p. 241 e sg. TORNA
9 G. Peano,
Sulla definizione di probabilità, Rend.
Acc. Lincei, S. 5, V. XXI, 1912. p.429. TORNA
10 L. Brillouin, Scienze and
information theory, Acad. Press, 1962. TORNA
11
G. Amata, S. Notarrigo, Energia e
Arnbienie, CUECM, 1992. TORNA